Aufgabe 1 Lösung Das Dosenrennen

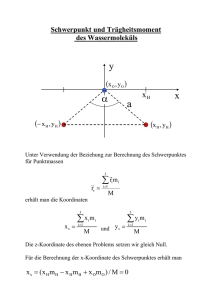
ForscherInnenwerkstatt Physik
Aufgabe 1
Graz, 02-2014
Lösung
Das Dosenrennen
Diese physikalischen Begriffe benötigt man:
Trägheitsmoment − Drehmoment − Kinetische Energie − Potentielle Energie − Energieerhaltung − Schiefe
Ebene
Abb. 1
1.2
Ergebnis:
Lässt man die so präparierten Dosen gleichzeitig aus der gleichen Höhe eine schiefe
Ebene hinunterrollen, so ist die Dose, deren Metallscheiben am Mittelpunkt des Dosenbodens befestigt sind (rechte Dose in Abb. 1)), schneller. Sie erreicht früher das untere Ende der schiefen
Ebene.
1.3
Erklärung:
Die linke Dose benötigt wegen des größeren Trägheitsmomentes („Schwungmas se“)
mehr Energie um sich in Drehung zu versetzen und daher bleibt ihr weniger Energie
für die
Geschwindigkeit bei der Abwärtsbewegung. Mit Hilfe zweier Dosen mit unterschiedlichem
Trägheitsmoment wird gezeigt, dass ein gleich großes Drehmoment bei einem Körper mit kleineTrägheitsmoment eine größere Winkelbeschleunigung hervorruft.
rem
Nur für SpezialistInnen:
Um zu begründen, warum die Dose mit dem kleineren Trägheitsmoment schneller ist, wird
die kinetische Energie der Dosen betrachtet. Die kinetische Energie der beiden Dosen in einer
bestimmten Höhe entspricht der potentiellen Energie, die sie bis zu dieser Höhe verloren haben. Da
die Masse der beiden Dosen gleich ist, haben sie in der gleichen Höhe auch dieselbe potentielle
Energie verloren:
1 2 1
1
1
mv1 + J1ω 12 = mv 22 + J 2ω 22
2
2
2
2
( vi : Betrag der Geschwindigkeit der Dose i (
); J i : Trägheitsmoment der Dose i; ω i :
Betrag der Winkelgeschwindigkeit der Dose i; m: Masse der Dosen)
v
ω i lässt sich ausdrücken durch: ω i = i . Damit erhält man:
r
2
2
1 2 1 ⎛ v1 ⎞
1
1 ⎛v ⎞
mv1 + J1 ⎜ ⎟ = mv 22 + J 2 ⎜ 2 ⎟ .
2
2 ⎝r⎠
2
2 ⎝ r⎠
schwindigkeiten:
v1
mr 2 + J 2
=
v2
mr 2 + J1
Daraus berechnet man das Verhältnis der Ge-
.
Daher besitzt die Dose mit dem kleineren Trägheitsmoment die größere Endgeschwindigkeit.
Quellenangabe:
Physikalische Freihandexperimente, 1997, Aulis-Verlag, D 85399 Hallbergmoos