DOC

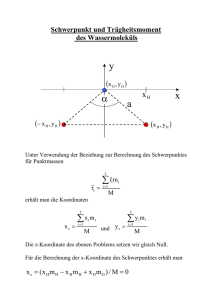
Schwerpunkt und Trägheitsmoment
des Wassermoleküls
y
x O , y O 

xH
a
 x H , yH 
x
x H , yH 
Unter Verwendung der Beziehung zur Berechnung des Schwerpunktes
für Punktmassen

 ri mi
3

rs 
i 1
M
erhält man die Koordinaten
3
xs 
x m
i 1
i
M
3
i
und y s 
y m
i 1
i
i
M
Die z-Koordinate des ebenen Problems setzen wir gleich Null.
Für die Berechnung der x-Koordinate des Schwerpunktes erhält man
x s  ( x H m H  x H m H  x O mO ) / M  0
Dieses Resultat war bereits aufgrund der Symmetrie des Problems zu
erwarten.
Für die y-Koordinate des Schwerpunktes folgt:
ys  2y H m H  yO mO  M
Gegeben seien der Winkel  = /2, der Abstand a sowie die relativen
Atommassen m1,2 = mH = 1 und m3 = mO = 16. Aus der Geometrie der
Anordnung erhält man
x H  x1, 2   a sin 
xO  x3  0
y H  y1, 2  a cos 
y3  0
Die (relative) Gesamtmasse beträgt M = 18.
Setzt man diese Werte in die Beziehung für ys ein, erhält man
ys 
yH
a cos 

9
9
Somit haben wir bezüglich unseres gewählten Koordinatensystems
folgende Schwerpunktkoordinaten:
 
a cos  
rs   0,
,0 
9


Damit liegt der Schwerpunkt SP sehr nahe beim Sauerstoffatom.
y
x O , y O 
SP
 x H , yH 
a
xH
x
x H , yH 
Will man die im Molekül gespeicherte Rotationsenergie berechnen,
benötigt man das Trägheitsmoment bezüglich der Rotationsachsen.
Freie Moleküle rotieren um ihre sogenannten Hauptträgheitsachsen.
Diese Achsen gehen durch den Schwerpunkt und sind so gerichtet,
dass die Trägheitsmomente extremal sind. Für eine (von 3
Hauptträgheitsachsen) Rotationsachse soll im folgenden das
Trägheitsmoment angegeben werden.
y
x O , y O 
SP
a
x
y H  ys
 x H , yH 


x H , yH 
Unter Verwendung von
3
I   ri2 m i
i 1
und
r1  rO  y s 
yH
9
8
yH
9
kann man das Trägheitsmoment berechnen. Man muss jetzt allerdings
die absoluten Atommassen verwenden. Im folgenden ist mit mH die
Protonenmasse gemeint. Durch Einsetzen erhält man:
r2  r3  rH  y H  y s 
I
144
m H a 2 cos 2 
81