Schulinternes Curriculum - Mathematik
Werbung

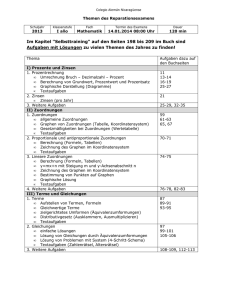
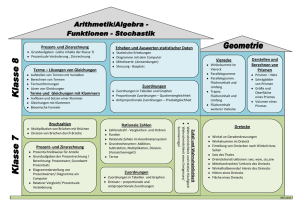
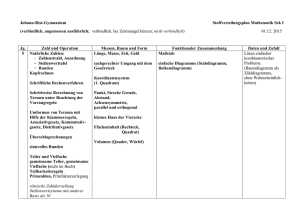
Schulinternes Curriculum Mathematik Klasse 7 Themen und Gegenstände des Unterrichts Kompetenzen Prozentrechnung → Grundwert, Prozentsatz, Prozentwert → Rabatt, Mehrwertsteuer, Hinweis auf Promille → Zinsrechnung und Zinseszins → Berechnung des Grundwertes mit Hilfe der Dreisatzes, Schlussrechnung → Anwendungsbezogene Textaufgaben Arithmetik/ Algebra Argumentieren/ Kommunizieren deuten eines Prozentsatzes als Anteil in den verschiedenen Darstellungsweisen für Brüche Gleichungen mit Hilfe von Formeln aufstellen und lösen Übersetzung des Textes in die einzelnen math. Größen Grundwert, Prozentwert und Prozentsatz, Deutung und Erklärung des Sachverhaltes sowie dessen Lösung Bedeutung der Begriffe „Erhöhung um“ bzw. „Erhöhung auf“ realisieren und den Unterschied kennen Problemlösen Verschiedene Modelle zur Problemlösung nutzen (Dreisatz, Gleichung) und ihren Nutzen bewerten Modellieren Einfache Realsituationen in mathematische Modelle fassen Nutzen der Grundfunktionen des neuen Taschenrechners: Grundrechenarten, Brüche Werkzeuge Einsatz von Tabellenkalkulationsprogrammen, um die Entwicklung bei Zinseszinsrechnung darzustellen Zuordnungen → Graphische und algebraische Darstellung von Zuordnungen als Vorbereitung für den Funktionsbegriff → Direkte Proportionalität, Quotientengleichheit, Ursprungsgerade Funktionen Arithmetik/ Algebra Zur Lösung außer- und innermathematischer Problemstellungen die Eigenschaften von proportionalen, antiproportionalen und lineare Zuordnungen sowie einfache Dreisatzverfahren anwenden. → Indirekte Proportionalität, Produktgleichheit, Hyperbel → Lineare Zuordnung, steigende/fallende Gerade, yAbschnitt als Ausgangswert, Steigungsfaktor als konstante Zunahme/Abnahme Zuordnungen mit eigenen Worten, Wertetabellen, als Graphen und in Termen darstellen und zwischen diesen Darstellungen wechseln. Graphen von Zuordnungen und Termen linearer funktionaler Zusammenhänge interpretieren. Identifizieren von proportionalen, antiproportionalen und linearen Zuordnungen in Tabellen, Termen und Realsituationen. Argumentieren/ Kommunizieren Muster und Beziehungen bei Zahlen erkennen, Lösungen auf Plausibilität überprüfen Problemlösen Einsatz von Tabellenkalkulationsprogrammen zur Überprüfung der Proprtionalität bzw. der graphischen Zusammenhänge Werkzeuge Nutzen weiterer Funktionen des GTR: Wertetballen aufstellen, Graphen geeignet darstellen (V-Window), TRACE, G-SOLV Terme → Termbegriff, Aufstellen und Interpretieren, Gliedern und Auswerten von Termen Arithmetik/ Algebra Blick für die algebraischen Zusammenhänge bei Termen entwickeln → Umformen von Termen, äquivalente Terme → Rechnen mit Termen, Klammerregeln, Ausmultiplizieren und Faktorisieren, D-Gesetz (allerdings noch nicht bei Summen) Terme zusammenfassen, ausmultiplizieren und sie mit einem einfachen Faktor faktorisieren. Argumentieren/ Kommunizieren Vorgehensweise zur Lösung eines Problems planen und beschreiben Problemlösen Möglichkeiten mehrerer Lösungen und Lösungswege bei Problemen überprüfen und deren Gleichwertigkeit erkennen Modellieren Einfache Realsituationen in mathematische Modelle übersetzen Gleichungen → Lösen von linearen Gleichungen mit einer Unbekannten mit Hilfe der Äquivalenzumformungen → Berechnung des Eingabewertes bei linearen Zuordnungen, Gleichung nach x auflösen → Sachaufgaben, Übersetzung des Textes in eine mathematische Gleichung Arithmetik/ Algebra Lineare Gleichungen lösen, sowohl durch Probieren als auch algebraisch und grafisch, Probe zur Rechenkontrolle. Kenntnisse über rationale Zahlen verwenden, um inner- und außermathematische lineare Gleichungen zu lösen. Argumentieren/ Kommunizieren Informationen aus Texten herauslesen Problemlösen Einem mathematischen Modell eine passende Realsituation zuordnen Modellieren Modelle verändern bzw. auf eine neue Situation anpassen Dreieckslehre → Konstruktion von Dreiecken incl. Konstruktionsbeschreibung → Kongruenzsätze → Transversalen im Dreieck, Umkreis, Inkreis, Schwerpunkt, Dreieckskonstruktionen → Winkel an Geradenkreuzungen, Doppelkreuzungen → Besondere Dreiecke: Gleichschenkliges Dreieck, Gleichseitiges Dreieck, Rechtwinkliges Dreieck Eigenschaften von Figuren erkennen und beweisen Geometrie Muster und Beziehungen bei Zahlen erkennen, Lösungen auf Plausibilität überprüfen Arithmetik/ Algebra ausformulieren von Beweisen Argumentieren/ Kommunizieren Problemlösen → Beweise in der Geometrie anhand der Winkelsumme präsentieren von Beweisen vermuten und verbalisieren allgemeiner Zusammenhänge Die bei Spezialfällen auftretenden Zusammenhänge auf allgemeine Situationen übertragen dynamische Geometriesoftware als heuristisches Hilfsmittel einsetzen im Dreieck, Basiswinkelsatz, Satz von Thales Werkzeuge Lineares Gleichungssystem → LGS mit zwei Unbekannten, graphische Interpretation der Lösungen über die Geradengleichungen, Arithmetik/ Algebra Terme zusammenfassen, ausmultiplizieren und sie mit einem einfachen Faktor faktorisieren. Blick für die algebraischen Zusammenhänge bei Termen entwickeln → Lösungsverfahren: Gleichsetzungsverfahren, Einsetzungsverfahren, Additionsverfahren Rechnen mit zwei Variablen Funktionen Zuordnungen mit eigenen Worten, Wertetabellen, als Graphen und in Termen darstellen und zwischen diesen Darstellungen wechseln. Graphen von Zuordnungen und Termen linearer funktionaler Zusammenhänge interpretieren. Verschiedene Lösungsmethoden miteinander vergleichen und deren Nutzen bewerten Problemlösen Übersetzung eines Textes in die Sprache der Mathematik Modellieren Lösen von Lin. GLS mit Hilfe des GTR