Brennpunkt der Parabel

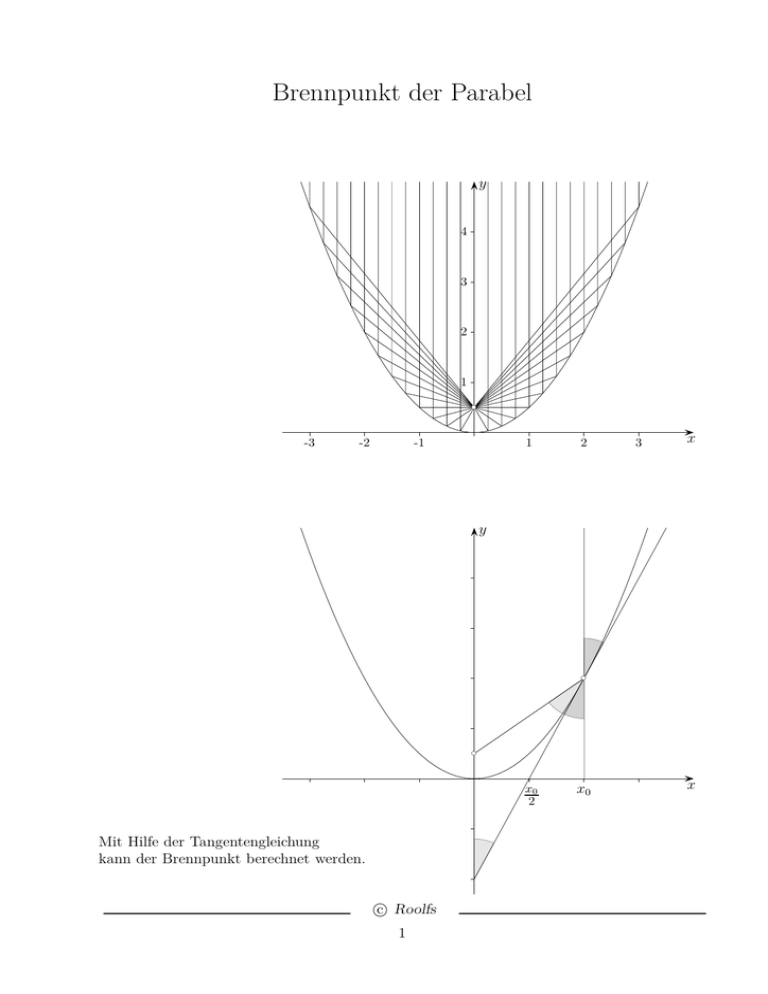
Brennpunkt der Parabel
y
4
3
2
1
bc
-3
-2
-1
1
2
3
x
y
bc
bc
x0
2
Mit Hilfe der Tangentengleichung
kann der Brennpunkt berechnet werden.
c Roolfs
1
x0
x
Brennpunkt der Parabel
y
f (x) = ax2
bc
bc
p
x0
2
x0
x
−ax20
Die Tangentengleichung t(x) = m(x − x0 ) + ax20
für f (x) = ax2 kann auch ohne Differentialrechnung ermittelt werden.
Berechne die Schnittstellen von f und t.
Ergebnis: x1 = x0 , x2 = m −aax0
x2 stimmt nur für m = 2ax0 mit x1 überein.
Die Tangente schneidet die x-Achse in x20 und die y-Achse in y = −ax20 .
Um das p und damit den Brennpunkt B(0 | p) zu ermitteln, ist die Gleichung
ax20 + p =
q
(ax20 − p)2 + x20
zu lösen (beachte das gleichschenklige Dreieck, alle eingezeichneten Winkel sind gleichgroß).
1
Ergebnis: p = 4a
p ist von x0 unabhängig.
1
Die Parabel f (x) = ax2 hat den Brennpunkt B 0 | 4a
.
Für jeden parallel zur y-Achse einfallenden Strahl verläuft der reflektierte Strahl durch B.
c Roolfs
2
Parabel als Ortslinie
y
P
bc
B
bc
x0
2
x
x0
A
y
P
bc
| AB | = | BP |
⇐⇒ | P B | = | P C |
B
bc
x
bc
C
Eine Parabel ist die Ortslinie aller Punkte P , die von einer Geraden g (Leitlinie)
und einem Punkt B (Brennpunkt) den gleichen Abstand haben.
c Roolfs
3
g
Parabel als Ortslinie
y
bc
bc
bc
bc
bc
bc
bc
bc
bc
bc
bc
bc
c Roolfs
4
bc
bc
x