1.1. Vorspiel bei den alten Griechen

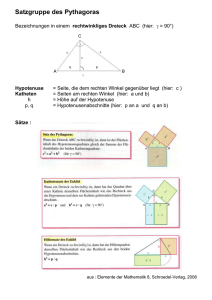
1.1. Vorspiel bei den alten Griechen
Die Mathematiker der griechischen Antike waren ihrer Zeit und auch ihren Epigonen im "finsteren
Mittelalter" um Etliches voraus. Einige ihrer Entdeckungen werden wir im Laufe dieser Vorlesung
kennen lernen.
Zu den großen mathematischen Denkern des Abendlandes gehören PYTHAGORAS, EUKLID und
der vielleicht genialste Ingenieur aller Zeiten, ARCHIMEDES. Geometrie und Ingenieurpraxis
waren für ihn untrennbar verbunden - und sollten es auch für den modernen Ingenieur sein!
Kreise und Dreiecke
Wir beginnen mit ein paar (hoffentlich) wohlbekannten Fakten aus der elementaren Geometrie:
Gleichung des Einheitskreises
in kartesischen Koordinaten:
x +y =1
2
in Parameterdarstellung:
x = cos( t ) , y = sin( t )
2
Allgemeine Kreisgleichung für Mittelpunkt m = ( m1, m2 ) und Radius r :
2
2
( x − m1 ) + ( y − m2 ) = r2
x = m1 + r cos( t ) ,
y = m2 + r sin( t )
Beispiel 1. Pythagoras auf dem Broadway
Nach einer Odyssee über den Atlantik gerät Pythagoras in das Großstadtgewimmel von New York.
Der Stadtteil Manhattan wird durch seine Straßen in Quadrate aufgeteilt - nur der Broadway
verläuft schräg durch das entstehende Gittermuster.
Wie lange ist der Broadway, wenn die Länge jedes Quadrates eine Meile beträgt?
Die Antwort gibt der berühmte
Satz des Pythagoras: Ein Dreieck ist genau dann rechtwinklig, wenn die Fläche des
Hypotenusenquadrats gleich der Summe der Flächen der Kathetenquadrate ist:
a2 + b2 = c2
Im Falle des Broadways als Hypotenuse erhalten wir für die Kathetenlängen a = 3 und b = 4 :
c=
32 + 42 = 25 = 5.
Geometrischer Beweis:
Landvermessung (schon im alten Ägypten, 2000 v. Chr.)
Ein geschlossenes Seil wird durch Knoten in 12 gleich lange Strecken aufgeteilt. Wählt man drei
Knoten im Abstand 3:4:5, so entsteht nach Spannen des Seils ein rechtwinkliges Dreieck. Damit
kann man rechteckige Felder abstecken.
32 + 42 = 52
Pythagoräische Tripel
a = x2 − y2 , b = 2 x y , c = x2 + y2
=> a2 + b2 = c2
Jedes solche Pythagoräische Tripel liefert ein rechtwinkliges Dreieck mit ganzzahligen
Seitenlängen!
Beispiel 2: Euklid im Amphitheater
Zur Uraufführung des Dramas "Ingenius und Elektra" drängen sich die Zuschauer auf den Stufen
des Amphitheaters, um den besten Blickwinkel auf die Bühne zu ergattern. Euklid bleibt gelassen:
weiß
er doch, daß man innerhalb einer kreisförmigen Reihe die Bühne stets unter dem gleichen Winkel
sieht, völlig unabhängig vom gewählten Platz. Der geometrische Hintergrund für diese Tatsache ist
der
Umkreiswinkelsatz des Euklid: Eine Sehne eines Kreises wird von allen Punkten des
Kreisrandes, die auf der gleichen Seite liegen, unter dem selben Winkel gesehen.
Beweis: Die Winkelsumme in einem Dreieck beträgt stets π = 1800 .
Speziell ist in dem nachfolgenden Bild
2 α + 2 β + 2 γ = π und
δ+2γ=π,
also α + β =
δ
2
konstant!
Ein Sonderfall des Umfangwinkelsatzes ist der
Satz des Thales: Von jedem Punkt eines Kreisrandes aus sieht man den Durchmesser unter einem
rechten Winkel.
Eine Ergänzung zum Umfangswinkelsatz müssen wir jetzt noch nachtragen: Die Zuschauer, die
nur auf der Rückseite der Bühne (im Bild unten) einen Platz gefunden haben, sehen diese (außer
im Falle des Thaleskreises) unter einem anderen Winkel als die auf der Vorderseite (im Bild oben);
und zwar ergänzen sich die beiden Blickwinkel gerade zu
π = 1800.
Das folgt aus dem Satz von Thales und der Tatsache daß die Winkelsumme in jedem Viereck
2 π = 3600
beträgt. Allgemein ist die Winkelsumme in einem beliebigen n-Eck
(n − 2) π .
Der Satz von Pythagoras folgt aus dem ebenfalls von Euklid stammenden
Kathetensatz: Für rechtwinklige Dreiecke ist die Fläche eines Kathetenquadrats gleich der Fläche
des Recktecks, das von dem zugehörigen Hypotenusenabschnitt und einer weiteren Seite des
Hypotenusenquadrats aufgespannt wird.
Beweis: Aus der Ähnlichkeit der rechtwinkligen Dreiecke ergibt sich
a c
=
, also a2 = p c.
p a
Ein "mechanischer" Beweis des Kathetensatzes:
Und von Euklid stammt auch der
Höhensatz: Für rechtwinklige Dreiecke ist das Höhenquadrat gleich dem Produkt der
Hypotenusenabschnitte.
Der Beweis ergibt sich wieder ganz leicht durch Betrachtung ähnlicher Dreiecke.
Der Beweis ergibt sich wieder ganz leicht durch Betrachtung ähnlicher Dreiecke.
h
p
=
q
h
=> h2 = p q