Physikinformationsblatt
Werbung
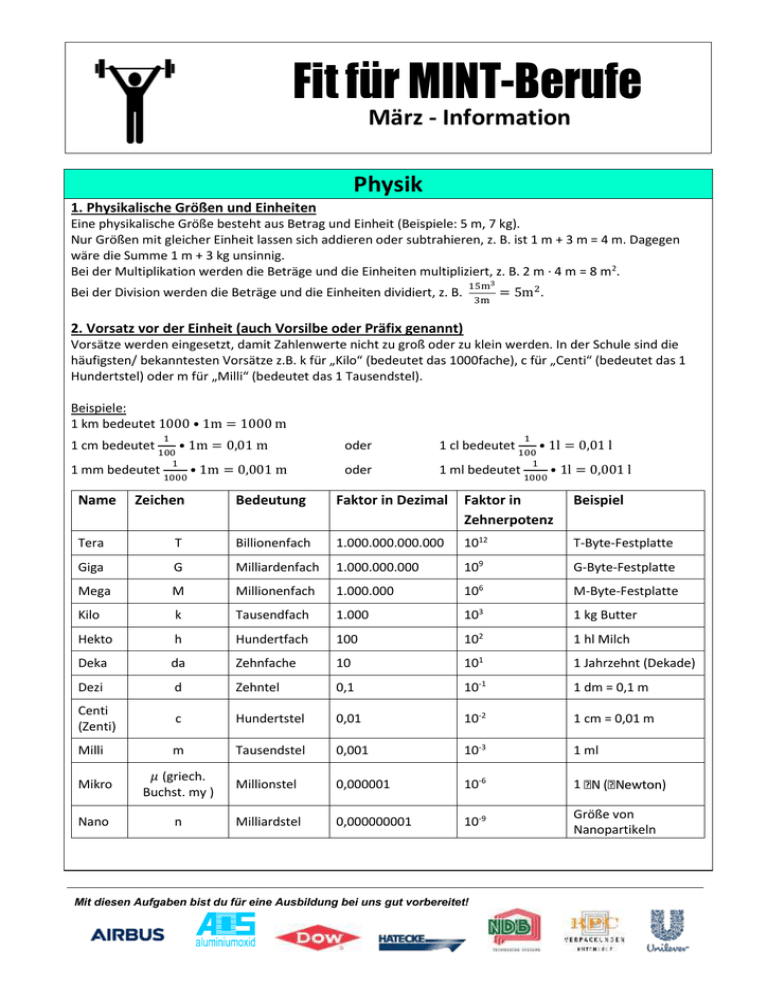
Fit für MINT-Berufe März - Information Physik 1. Physikalische Größen und Einheiten Eine physikalische Größe besteht aus Betrag und Einheit (Beispiele: 5 m, 7 kg). Nur Größen mit gleicher Einheit lassen sich addieren oder subtrahieren, z. B. ist 1 m + 3 m = 4 m. Dagegen wäre die Summe 1 m + 3 kg unsinnig. Bei der Multiplikation werden die Beträge und die Einheiten multipliziert, z. B. 2 m ∙ 4 m = 8 m 2. 15m3 3m Bei der Division werden die Beträge und die Einheiten dividiert, z. B. = 5m2. 2. Vorsatz vor der Einheit (auch Vorsilbe oder Präfix genannt) Vorsätze werden eingesetzt, damit Zahlenwerte nicht zu groß oder zu klein werden. In der Schule sind die häufigsten/ bekanntesten Vorsätze z.B. k für „Kilo“ (bedeutet das 1000fache), c für „Centi“ (bedeutet das 1 Hundertstel) oder m für „Milli“ (bedeutet das 1 Tausendstel). Beispiele: 1 km bedeutet 1000 • 1m = 1000 m 1 • 1m = 0,01 m 100 1 bedeutet • 1m = 0,001 1000 1 cm bedeutet 1 mm Name Zeichen m 1 • 1l = 0,01 l 100 1 bedeutet • 1l = 0,001 l 1000 oder 1 cl bedeutet oder 1 ml Bedeutung Faktor in Dezimal Faktor in Zehnerpotenz Beispiel Tera T Billionenfach 1.000.000.000.000 1012 T-Byte-Festplatte Giga G Milliardenfach 1.000.000.000 109 G-Byte-Festplatte Mega M Millionenfach 1.000.000 106 M-Byte-Festplatte Kilo k Tausendfach 1.000 103 1 kg Butter Hekto h Hundertfach 100 102 1 hl Milch Deka da Zehnfache 10 101 1 Jahrzehnt (Dekade) Dezi d Zehntel 0,1 10-1 1 dm = 0,1 m Centi (Zenti) c Hundertstel 0,01 10-2 1 cm = 0,01 m Milli m Tausendstel 0,001 10-3 1 ml Mikro 𝜇 (griech. Buchst. my ) Millionstel 0,000001 10-6 1 Nano n Milliardstel 0,000000001 10-9 Größe von Nanopartikeln Mit diesen Aufgaben bist du für eine Ausbildung bei uns gut vorbereitet! Fit für MINT-Berufe März - Information 3. Zusammenhang zwischen Geschwindigkeit , Strecke und Zeit: Geschwindigkeit v beschreibt, wie schnell ein Körper ist, also welche Strecke s ein Körper in einer bestimmten Zeit t zurücklegt. Angegeben wird die Geschwindigkeit v in Umrechnung der Einheiten: km h m s ∶ 3,6 = • 3,6 = m Beispiel: 36 s km Beispiel: 20 h km h m s Bezeichnung Formelzeichen Einheit Geschwindigkeit v m km , s h Strecke s m Zeit t s km h m und s . ∶ 3,6 = 10 • 3,6 = 72 m s km h Berechnung/ Formel 𝑠 𝑣= 𝑡 𝑠 =𝑣•𝑡 𝑠 𝑡= 𝑣 4. Zusammenhang von Masse, Volumen und Dichte: Ein Körper hat ein Volumen V in m3 und eine Masse m in kg. Wenn man wissen will, ob der Körper schwimmt oder in der Luft schwebt, kommt es darauf an, wie groß die Masse pro Volumen ist. Dieser Quotient heißt Dichte. Das Formelzeichen ist der griechische Buchstabe „rho“ oder ρ. Bezeichnung Formelzeichen Einheit Volumen V m3 Masse m kg Dichte ρ kg m3 Umrechnung der Einheiten: kg kg g 1000 m3 = 1 dm3 = 1 cm3 kg 1000 m3 = 1 kg l =1 g ml (l: Liter, ml: Milliliter) Mit diesen Aufgaben bist du für eine Ausbildung bei uns gut vorbereitet! Berechnung/ Formel 𝑚 𝑉= 𝜌 𝑚 =𝑉•𝜌 𝜌= 𝑚 𝑉 Fit für MINT-Berufe März - Information 5. Zusammenhang beim elektrischen Stromkreis zwischen Spannung, Stromstärke und Widerstand: Glühlampe (Verbraucher) Elektronen Spannungsquelle Ein Stromkreis wird in einer Schaltskizze dargestellt. Ein einfacher Stromkreis besteht aus einer Spannungsquelle und einem Verbraucher, wobei Spannungsquelle und Verbraucher durch Kabel einen geschlossenen Stromkreis bilden. Durch den Stromkreis fließen bewegliche elektrische Teilchen, die Elektronen. Diese werden durch eine Spannungsquelle mit einer Spannung U angetrieben. So entsteht eine Stromstärke I. Der Verbraucher hat einen Widerstand R, der die Stärke des Stromflusses begrenzt. Bezeichnung Formelzeichen Einheit Stromstärke I A Spannung U V Widerstand R Ω (A: Ampere, Ω: Ohm, V: Volt) Umrechnung der Einheiten: 1A = 1 V Ω 1Ω = 1 V A Berechnung/ Formel 𝑈 𝐼= 𝑅 𝑈 =𝑅•𝐼 𝑈 𝑅= 𝐼 1V = 1Ω ∙ A 6. Zusammenhang von Masse, Ortsfaktor und Gewichtskraft: Die Erde zieht Massen an. Man sagt, bei der Erde wirkt eine Gewichtskraft FG auf eine Masse m. Die Gewichtskraft FG ist gleich das Produkt aus der Masse m und einem Faktor g, kurz FG = m∙g. Beim Mond wirkt auf die gleiche Masse m eine schwächere Gewichtskraft, also ist beim Mond der Faktor g kleiner. Daher nennt man den Faktor g korrekterweise Ortsfaktor. N N Bei der Erde ist g = 9,81 kg (Näherung: g ≈ 10 kg ). Bezeichnung Formelzeichen Ortsfaktor g Gewichtskraft FG Einheit N kg N Masse m kg (N: Newton) Mit diesen Aufgaben bist du für eine Ausbildung bei uns gut vorbereitet! Berechnung/ Formel 𝐹𝐺 𝑔= 𝑚 𝐹𝐺 = 𝑚 • 𝑔 𝐹𝐺 𝑚= 𝑔 Fit für MINT-Berufe März - Information 7. Zusammenhang von Hebelarm, Kraft und Drehmoment: Die Abbildung zeigt einen zweiseitigen Hebel. Kraft F2 Du kennst das Gleichgewicht auf der Wippe: Zwei Personen mit unterschiedlichen Massen können dieses Gleichgewicht herstellen. Es ist somit kein Massengleichgewicht. Beide Personen üben unterschiedliche Gewichtskräfte F1 und F2 auf die Wippe aus. Es ist also auch kein Kräftegleichgewicht. Was ist das für ein Gleichgewicht? Dazu überlegen wir uns, was bei beiden Personen gleich ist. Es ist das Produkt aus Gewichtskraft F und Hebelarm l. Der Hebelarm ist die Entfernung zum Drehpunkt. Daraus ergibt sich das Hebelgesetz: F1 ∙ l1 = F2 ∙ l2 Dieses Produkt nennt man das Drehmoment M. Daraus ergibt sich: M1 = F1 ∙ l1 und M2 = F2 ∙ l2 sowie das Hebelgesetz M1 = M2 Bezeichnung Formelzeichen Einheit Hebelarm l m Drehmoment M Nm Kraft F N Berechnung/ Formel 𝑀 𝑙= 𝐹 𝑀 =𝐹•𝑙 (Nm: Newtonmeter) Schubkarre: Beim einseitigen Hebel befinden sich beide Kräfte auf der gleichen Seite des Drehpunktes: l2 l1 Mit diesen Aufgaben bist du für eine Ausbildung bei uns gut vorbereitet! 𝐹= 𝑀 𝑙