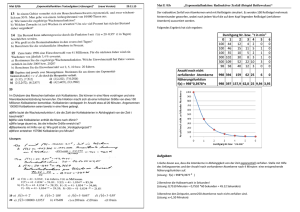
tfd tfc tfb tfa 95,03 ) 667,05 ) 06,12 ) 24 ) ∙ = ∙ = ∙ = ∙ = min 110) min 20

Mat E/Gb
„Exponentialfunktion: Textaufgaben (+Lösungen)“
(neue Version)
01.12.11
20
Im Dickdarm des Menschen befinden sich Kolibakterien. Sie können in eine Niere vordringen und eine
Nierenbeckenentzündung hervorrufen. Die Infektion macht sich ab einer kritischen Größe von etwa 100
Millionen Kolibakterien bemerkbar. Kolibakterien verdoppeln ihr Anzahl etwa all 20 Minuten. Angenommen
100000 Kolibakterien seien bereits in eine Niere gelangt.
a)Wie lautet die Wachstumsfunktion f, die die Zahl der Kohlebakterien in Abhängigkeit von der Zeit t
beschreibt?
b)Wie viele Kolibakterien enthält die Niere nach 45min?
c)Wie lange dauert es, bis die kritische Größe erreicht ist?
d)Beantworte mit Hilfe von a): Wie groß ist die „Verdopplungszeit“?
e)Wann entstehen 157580 Kolibakterien pro Minute?
Lösungen:
19 a) f t   4  2t
b) f t   2  1,06t
b) 476409
20 a) f t   100000  1,0353t
c) f t   5  0,667t
d ) f t   3  0,95t
c) ca.200 min d )20 min
e)110 min
Mat E /Gb
„Exponentialfunktion: Radioaktiver Zerfall (Beispiel Reißzwecken)“
Der radioaktive Zerfall von Atomkernen wird mit Reißnägeln simuliert. Es werden 100 Reißnägel mehrmals
hintereinander geworfen, wobei nach jedem Wurf die auf dem Kopf liegenden Reißnägel (zerfallener
Atomkern) aussortiert werden.
Folgendes Ergebnis hat sich ergeben:
Anzahl noch nicht
zerfallender Atomkerne
Näherungsfunktion
f(x) = 998*0,3978^x
Durchgang Nr. bzw. "t in min"
0
1
2
3 4
5
100 44
12
4 2
0
100 46
15 11 5
1
100 35
10
5 2
1
300 102
30
8 3
1
300 109
52 22 10
3
98 58
40 12 3
0
6
0
0
0
0
0
0
998 394
0
159
62 25
6
998 397 157,9 62,8 25 9,94 3,95
Aufgaben:
1.Gehe davon aus, dass die Atomkerne in Abhängigkeit von der Zeit exponentiell zerfallen. Stelle mit Hilfe
des Anfangswertes und der Anzahl noch vorhandener Atomkerne nach 4 Minuten eine entsprechende
Näherungsfunktion auf.
(Lösung: f(x) = 998*0,3977
x
)
2.Berechne die Halbwertszeit in Sekunden!
(Lösung: 0,7510 Minuten = 0,7510 *60 Sekunden = 45.12 Sekunden)
3.Berechne den Zeitpunkt, wenn250 Atomkerne noch nicht zerfallen sind.
(Lösung: x=1,50 Minuten)