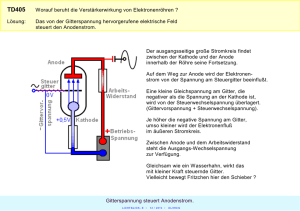
Erläuterungen und weiterführende Informationen zu den

Erläuterungen und weiterführende Informationen zu den thermodynamischen Grundlagen des Versuchs "Galvanisches Element" (zu lesen nach Durchführung des Versuchs)
Analogie zwischen der isothermen Expansion eines Gases und der Entladung des
Cadmium/Cadmiumamalgam-Elements
Betrachten Sie bitte einen Carnot'schen Kreisprozess mit einem idealen Gas als Arbeitsmedium.
Der erste Takt des Carnot'schen Kreisprozesses ist eine isotherme Expansion. Dabei fließt Wärme q
aus einem Reservoir in das Arbeitsgas, q >0, während Volumenarbeit wvol an die Umgebung abgegeben wird und sich dort z.B. als potentielle Energie in einem Gewicht speichern lässt, wvol <0. Da
die Temperatur konstant gehalten wird, bleibt die Innere Energie des idealen Arbeitsgases unverändert. Nach dem Ersten Hauptsatz der Thermodynamik gilt also ΔU = 0 = q + w vol und damit
-wvol = q.
Bis hierher ist über die Reversibilität des Prozesses noch nichts gesagt worden. Es ist bekannt, dass
die geleistete Volumenarbeit davon abhängt, ob eine Expansion reversibel, (schwach) irreversibel
oder vollständig irreversibel geführt wird. Je irreversibler die Expansion bei festem Anfangs- und
festem Endzustand geführt wird, umso kleiner wird der Betrag von wvol, aber stets so, dass -wvol = q
bleibt. Man erkennt, dass in dem Expansionstakt Wärme mit dem vollen Wirkungsgrad von 100 %
in mechanische Arbeit umgewandelt wird, und zwar unabhängig vom Ausmaß der Irreversibilität.
(Ein Widerspruch zum Zweiten Hauptsatz liegt selbstverständlich nicht vor, denn der Zweite
Hauptsatz macht einschränkende Aussagen über den Wirkungsgrad nur von kompletten Kreisprozessen.)
Ist der Expansionsprozess vollständig irreversibel (das Gas expandiert dann einfach in ein Vakuum), wird die Volumenarbeit natürlich gleich Null, man muss allerdings auch keine Wärme mehr
zuführen, so dass -wvol = q sogar in diesem Grenzfall gilt.
Möglicherweise bereitet Ihnen die Vorstellung eines isothermen Prozesses, bei dem Wärme auftritt,
Schwierigkeiten, denn Wärme ist als Energiefluss durch die Systemgrenzen als Folge eines Temperaturgradienten definiert. Vielleicht nehmen Sie sogar zu Unrecht an, dass Wärme notwendigerweise am Zielort zu einer Temperaturerhöhung führen müsse.
Zur Klärung denken Sie zunächst an eine unter konstantem Druck siedende Flüssigkeit. Die Temperatur ist stets gleich der Siedetemperatur der Flüssigkeit, obwohl große Mengen Wärme in das System hineinströmen. Das Ziel, eine bestimmte Menge der Flüssigkeit zu verdampfen, lässt sich theo-
retisch mit einer beliebig kleinen Temperaturdifferenz ΔT zwischen System (siedende Flüssigkeit)
und Wärmequelle (z.B. elektrische Heizplatte) erreichen, wenn zur Kompensation die Dauer des
Experiments entsprechend verlängert wird. Strebt ΔT gegen Null, steigt die Dauer des Experiments
gegen unendlich (was in einem thermodynamischen Gedankenexperiment nicht weiter stört), und in
der Grenze wird dieser isobare Prozess reversibel isotherm.
Bei der isothermen Expansion eines Gases sind die Verhältnisse etwas verwickelter, weil ein solcher Prozess natürlich nicht isobar ist. Denken Sie sich jetzt den Prozess als Folge von Doppelschritten, bestehend jeweils
●
aus einem adiabatische Schritt, bei dem das Gas expandiert, Expansionsarbeit auf Kosten
seiner Inneren Energie leistet und dabei kälter wird (q1 = 0, wvol,1 <0, ΔT1 <0 ),
●
und aus einem isochoren Schritt, bei dem die Temperatur des Gases durch Wärmezufuhr auf
ihren vorherigen Wert zurückgeführt wird (q2 > 0, wvol,2 = 0, ΔT2 = -ΔT1 >0 ).
Da die Endtemperatur in einem solchen Doppelschritt gleich der Anfangstemperatur ist, also beim
idealen Gas auch die Innere Energie ihren vorherigen Wert wieder erreicht, gilt nach dem Ersten
Hauptsatz -wvol,1 = q2 in jedem Doppelschritt. Nun erhöht man die Zahl der Doppelschritte und
lässt -ΔT1 und ΔT2 gegen Null gehen, wodurch ein Gesamtvorgang mit -wvol = q entsteht, der in
der Grenze isotherm ist, allerdings auch wieder unendlich lange dauert.
In Abb. 1 sind Wärme und Volumenarbeit für die isotherme Expansion eines idealen Gases bei festem Anfangs- und festem Endzustand als Funktion der Reversibilität der Expansion dargestellt. Wie
oben dargelegt, gilt unabhängig vom Ausmaß der Irreversibilität stets das Gleichheitszeichen in
-wvol = q. Weiter sind noch die folgenden Spezialfälle von Interesse:
●
der vollständig irreversible Fall, -wvol = q = 0,
●
und der reversible Fall, wo wegen dS = dqrev/T geschrieben werden darf
-wvol = q = TΔS
(T = konst.)
(1).
Es ist ganz wichtig einzusehen, dass das zweite Gleichheitszeichen der Gleichung (1) im irreversiblen Fall nicht gilt, weil |wvol| und q dann von ihren Werten im reversiblen Fall abweichen, während TΔS als Ausdruck, der nur Zustandsgrößen enthält, selbstverständlich unabhängig vom Ausmaß der Irreversibilität ist.
Abb. 1: Wärme und Volumenarbeit bei der isothermen Expansion eines idealen Gases
(ΔU=0); schematisch
Die Größe w im Ersten Hauptsatz, ΔU = q + w, umfasst prinzipiell alle Sorten von Arbeit. Die spezielle Form ΔU = q + wvol durfte oben benutzt werden, weil bei einem idealen Gas neben der Volumenarbeit sicher keine weitere Sorte von Arbeit auftreten kann. Wenn wir nun aber galvanische
Elemente thermodynamisch behandeln wollen, muss natürlich in w die elektrische Arbeit mitgeführt werden, w = wvol + wel. Durch Kombination des Ersten Hauptsatzes ΔU = q + wvol + wel
mit der Enthalpie H = U + pV, für isobare Prozesse also ΔH = ΔU + pΔV, erhält man leicht(1)
ΔH = q + wel
(p = konst.)
(2).
Die häufig benutzte Beziehung ΔH = q (bei konstantem Druck) gilt also wie ΔU = q + wvol nur für
Systeme, in denen neben der Volumenarbeit keine andere Sorte von Arbeit auftritt.
Beachten Sie bitte, dass sich die Kriterien "exotherm" bzw. "endotherm" definitionsgemäß auf das
Vorzeichen von q beziehen und nicht auf das von ΔH, und dass die Vorzeichen von q und ΔH beim
Auftreten von Nichtvolumenarbeit nicht mehr identisch sein müssen. Wenn also z.B. bei einer isotherm geführten Elektrolyse (wel > 0) Wärme aus der Elektrolysierzelle an die Umgebung abgegeben wird (q < 0 ) und dabei wel > -q gilt, hat die exotherme Reaktion positives ΔH. In Worten: Die
Enthalpie des Systems steigt, weil die zugeführte elektrische Arbeit die abgeführte Wärme überkompensiert.
Die Reaktionsenthalpie ΔH der Zellreaktion Cd + Hg → Cd(Hg) des im Praktikum untersuchten
Cadmium/Cadmium-Amalgam-Elements ist ca. -3 kJ/mol und hat damit einen ganz ungewöhnlich
kleinen Betrag. Das überrascht deshalb nicht, weil es sich ja gar nicht um eine echte chemische Reaktion handelt; das "Produkt" Cadmium-Amalgam kann sogar durch eine einfache Destillation
wieder in die "Edukte" Cadmium und Quecksilber getrennt werden. Würde man die Zellreaktion
kalorimetrisch verfolgen, fände man für diesen Prozess in der Tat eine kaum messbare exotherme
Wärmetönung. Vergleichen Sie diese Situation z.B. mit der Standardverbrennungsenthalpie der Glucose von ca. -2800 kJ/mol.
Im folgenden wollen wir eine Modellreaktion betrachten, die als Zellreaktion in einem galvanischen
Element ablaufen kann und deren Reaktionsenthalpie ΔH exakt gleich Null ist. Die Reaktionsentropie ΔS muss dann auf jeden Fall positiv sein (wieso?). Es gilt, in gewisser Analogie zu den oben am
Carnot'schen Kreisprozess hergeleiteten Beziehungen (jetzt immer bei konstantem Druck)
●
in -wel = q das Gleichheitszeichen unabhängig vom Ausmaß der Irreversibilität,
●
i.b. wel = q = 0 im vollständig irreversiblen Fall,
●
-wel = -ΔG und q = TΔS, also -wel = TΔS im reversiblen Fall.
Abb. 2: Wärme und elektrische Arbeit bei der reversiblen Entladung eines galvanischen
Elements, bei dem zufällig die Reaktionsenthalpie der Zellreaktion verschwindet (ΔH=0);
schematisch
In Abb. 2 sind Wärme und elektrische Arbeit für eine solche Modellreaktion bei festem Anfangsund festem Endzustand als Funktion der Reversibilität der Reaktion dargestellt. Beachten Sie die
Analogie zur Abb. 1. Die Modellreaktion (und damit näherungsweise auch das im Praktikum verwendete Cadmium/Cadmium-Amalgam-Element) ist theoretisch in der Lage, Wärme unabhängig
vom Ausmaß der Irreversibilität zu 100 % in elektrische Arbeit umzuwandeln, selbstverständlich
auch hier ohne Widerspruch zum zweiten Hauptsatz.
Um es nochmals ganz klar zu machen: Für unsere Modellreaktion hat unabhängig vom Ausmaß der
Irreversibilität die Größe -ΔG = TΔS immer den gleichen positiven Wert, und abhängig vom Ausmaß der Irreversibilität die Größe -wel = q einen variablen Wert größer oder gleich Null; in der
Gleichung
-ΔG = TΔS = -wel = q
(3)
gilt das zweite Gleichheitszeichen demgemäß nur im reversiblen Fall.
Während die praktische Durchführung des Carnot'schen Kreisprozesses mit einem variablen Ausmaß von Irreversibilität enorme technische Schwierigkeiten bereiten würde, ist die Entladung unseres galvanischen Elements hinsichtlich ihrer Irreversibilität leicht durch die Größe des Arbeitswiderstandes zu steuern. Ist der Arbeitswiderstand sehr groß (z.B. 100 MΩ = 108 Ω), unterscheidet
sich die Klemmspannung Ekl des Cadmium/Cadmium-Amalgam-Elements im Praktikum um weniger als 5 μV (<0.01 %) von der Spannung im elektrochemischen Gleichgewicht. Denn legt man
eine äußere Quelle mit derselben Polarität wie die des galvanischen Elements an, aber mit einer
Spannung, die um weniger als 10 μV höher liegt als Ekl, dreht sich die Stromrichtung bereits um,
und man beobachtet, unter Umkehr der Zellreaktion, eine (wenn auch extrem langsame) Wiederaufladung der Zelle durch Elektrolyse. Für das Wiederaufladen muss nur ganz geringfügig mehr Energie aufgewendet werden, als man vorher der Zelle durch Entladen entnommen hat. Das ist in sehr
guter Näherung reversibel!
Bei einem Arbeitswiderstand von 1 kΩ ist die Klemmspannung dieser Zelle nur noch ungefähr halb
so groß wie die Spannung im elektrochemischen Gleichgewicht, damit ist auch die molare elektrische Arbeit nur noch halb so groß wie ΔG. (Da die Abb. 2 ohnehin nur schematisch zu interpretieren ist, kann man sich auf der Abszisse den Logarithmus des Arbeitswiderstandes aufgetragen
denken, gegen den die Zelle arbeitet. Bemerkung für Experten: Dies gilt, solange der äußere Arbeitswiderstand deutlich größer ist als der Innenwiderstand der Zelle einschließlich des Durchtrittswiderstandes an den Elektroden.) Bei einem solchen kleinen Arbeitswiderstand braucht man für das
Wiederaufladen mindestens doppelt soviel Energie, wie man vorher beim Entladen entnommen hat.
Der Differenzbetrag muss einer äußeren Quelle entnommen werden, der Entladeprozess ist also irreversibel!
Abb. 3: Wärme und elektrische Arbeit bei der reversiblen Entladung eines galvanischen
Elements mit ΔH<0 und ΔS<0); schematisch
Verbindet man schließlich die beiden Elektroden direkt durch einen dicken Kupferdraht, verschenkt
man die ganze elektrische Energie, die man hätte gewinnen können, und das Wiederaufladen muss
vollständig auf Kosten einer äußeren Quelle geschehen: der Prozess ist vollständig irreversibel, in
Analogie zur Expansion eines Gases ins Vakuum.
In Abb. 3 sind Wärme und elektrische Arbeit für eine etwas allgemeinere Reaktion bei festem Anfangs- und festem Endzustand als Funktion der Reversibilität der Reaktion dargestellt. (Die Vorzeichen ΔH<0 und ΔS<0 würden z.B. für die Knallgasreaktion als Grundlage einer Brennstoffzelle zutreffen.) Wie man leicht beweisen kann, gilt bei Wegfall der Bedingung ΔH = 0, ansonsten aber entsprechend (2)
ΔG = ΔH - TΔS = wel = ΔH - q
mit dem zweiten Gleichheitszeichen nur im reversiblen Fall (also im ständigen elektrochemischen
Gleichgewicht).
Das elektrochemische Gleichgewicht
Der Begriff elektrochemisches Gleichgewicht ist bereits im vorigen Kapitel bei der Illustration der
Reversibilität verwendet worden. Wir wollen ihn jetzt nochmals etwas systematischer betrachten.
Das chemische Potenzial(2) des Cadmiums in der Cadmium-Elektrode ist größer als das chemische
Potenzial des Cadmiums in der Cadmiumamalgam-Elektrode, denn in letzterer ist das Cadmium im
Quecksilber gelöst und damit "verdünnt". Das Cadmium in der Cadmium-Elektrode hat eine
Tendenz, in das Quecksilber überzugehen, weil dadurch die freie Enthalpie als mengengewichtete
Summe aller chemischen Potenziale des Systems minimiert wird(3). Bringt man Cadmium und
Quecksilber in direkten Kontakt, folgt das Cadmium dieser Tendenz ungehemmt und löst sich im
Quecksilber auf.
In unserem galvanischen Element stehen die Cadmium-Elektrode und das Amalgam nicht in direktem Kontakt, sondern sind durch den Elektrolyten (Cadmiumchlorid in Wasser) getrennt. Ein Cadmium-Atom als solches kann aber, um zum Quecksilber zu gelangen, in die wässrige Lösung nicht
eintreten. Es muss zum Cadmium-Ion werden und kann erst dann als hydratisiertes Ion den
Elektrolyten durchqueren. Für jedes entstehende Cadmium-Ion bleiben dabei zwei Elektronen in der
Cadmium-Elektrode zurück. (Die Cadmium-Elektrode ist die Anode, weil dort das Cadmium-Atom
zum Cadmium-Ion oxidiert wird.) Angelangt an der Amalgamelektrode, stellt sich für das Cadmium-Teilchen das umgekehrte Problem: es kann als hydratisiertes Ion kann nicht in das Quecksilber
eintreten, sondern muss dazu die Hydrathülle abwerfen und sich wieder in das Atom zurückverwandeln. Für jedes ankommende Cadmium-Ion werden dabei zwei Elektronen an der Cadmiumamalgam-Elektrode verbraucht. (Die Amalgam-Elektrode ist die Kathode, weil dort das Cadmium-Ion zum Cadmium-Atom reduziert wird.)
Der entscheidende Aspekt dieses Vorgangs ist, dass hier ein Cadmium-Atom seiner Tendenz, sich
im Quecksilber aufzulösen, nur dadurch nachkommen kann, dass es sich erst an der Anode einer
Ladungstrennung unterwirft, die dann an einem räumlich getrennten Ort, nämlich an der Kathode,
rückgängig gemacht wird. Die entstehenden positiven und negativen Ladungsträger (CadmiumIonen und Elektronen) können nur auf getrennten Wegen von der Anode zur Kathode laufen: die
Ionen wie geschildert durch die Lösung, die Elektronen durch einen äußeren Stromkreis, in dem sie
z.B. mit einem kleinen Elektromotor Nutzarbeit verrichten können. Die Anode "schiebt" die Elektronen durch den Motor, prinzipiell gleichberechtigt "zieht" die Kathode die Elektronen durch den
Motor. Die Anode ist negativ, weil die Cadmium-Ionen von ihr wegwandern. Die Kathode ist positiv, weil die Cadmium-Ionen zu ihr hinwandern.
Unter einem streng energetischen Aspekt wird die Nutzarbeit im äußeren Stromkreis durch die Tendenz des Cadmiums aufgebracht, sich im Quecksilber aufzulösen. Ursächlich genauso wichtig für
die Realisierbarkeit einer elektrischen Nutzarbeit ist aber das Auftreten der Ladungstrennung, die
dadurch erzwungen wird, dass
●
Cadmium-Ionen nur in der wässrigen Lösung, nicht aber im Innern der metallischen
Elektroden
●
Cadmium-Atome nur in den metallischen Elektroden, nicht aber in der wässrigen Lösung
●
Elektronen nur im Innern der metallischen Elektroden und des sie verbindenden Leiters,
nicht aber in der wässrigen Lösung
vorkommen und ggf. wandern können.
Die Vorstellung, dass die Cadmium-Ionen zur Kathode wandern, weil sie dort von den Elektronen
angezogen werden, die die Cadmium-Ionen vorher an der Anode abgegeben haben, dass also an der
Kathode eine Art "Selbstelektrolyse" ablaufe, ist grob falsch. (Für Experten: die Vorstellung ist solange grob falsch, wie der äußere Arbeitswiderstand deutlich größer ist als der Innenwiderstand der
Zelle einschließlich des Durchtrittwiderstandes an den Elektroden ist. Nur unter dieser Bedingung
lässt sich aber ein galvanisches Element vernünftig einsetzen.)
Trennt man die elektrische Verbindung im äußeren Stromkreis und unterbindet so die Wanderung
der Elektronen, geht die Wanderung der Cadmium-Ionen zur Amalgam-Elektrode zunächst weiter.
Aber: jedes Cadmium-Teilchen, das an der Amalgam-Elektrode ankommt, hinterlässt in der Anode
zwei negative Elementarladungen, von wo sie jetzt nicht mehr abfließen können, und transportiert
zwei positive Elementarladungen, also zwei Elektronenlöcher zur Kathode, wo die Elektronenlöcher jetzt nicht mehr aufgefüllt werden können. Dadurch steigt der Unterschied des elektrischen Potenzials zwischen Kathode und Anode an und macht es den Cadmium-Teilchen zunehmend schwerer, ihrem Drang zum Amalgam nachzugeben. Denn als positive Ionen unterlegen sie einer
elektrostatischen Anziehung durch die negative Cadmium-Elektrode, von der sie doch aus Gründen
des chemischen Potenzials wegwandern wollen, und einer elektrostatischen Abstoßung durch die
positive Cadmiumamalgam-Elektrode, zu der sie doch aus Gründen des chemischen Potenzials hinwandern wollen. Wir haben also zwei entgegengesetzte Tendenzen zu berücksichtigen:
●
die Tendenz der Cadmium-Teilchen, von der Cadmium-Elektrode zur CadmiumamalgamElektrode zu wandern und dadurch einer verallgemeinerten "chemischen Kraft" zu folgen,
die in Richtung der Verringerung des chemischen Potenzials wirkt, und
●
die Tendenz der Cadmium-Teilchen, von der Cadmiumamalgam-Elektrode zur CadmiumElektrode zu wandern und dadurch der elektrischen Kraft zu folgen, die in Richtung des
Gradienten des elektrischen Potentials wirkt.
Der Unterschied der elektrischen Potenziale von Kathode und Anode steigt solange an, bis der Betrag der elektrischen Kraft genauso groß geworden ist wie der Betrag der "chemischen Kraft". Dann
haben wir elektrochemisches Gleichgewicht. In diesem speziellen Gleichgewichtszustand ist der
(als Zellspannung E gemessene) Unterschied E = φCd(Hg) - φCd der elektrischen Potenziale der
beiden Elektroden ein Maß für den Unterschied der chemischen Potenziale des Cadmiums in den
beiden Elektroden und damit(3) für die Freie Reaktionsenthalpie ΔG, nämlich
ΔG = μCd(Hg) - μCd = wel = - z F E.
Diese Formel verbindet auf schöne und verblüffend einfache Weise ΔG und μ als hochabstrakte
Größen der Thermodynamik mit E als einer experimentell leicht zugänglichen Größe der Elektrochemie.
Weiterführende Literatur
A.J.Bard, L.R.Faulkner, Electrochemical Methods, Fundamentals and Applications, Wiley, 2. Aufl. 2001
C. H. Hamann, W. Vielstich, Elektrochemie, Wiley-VCH, 3. Aufl. 1998
G. Kortüm, Lehrbuch der Elektrochemie, Verlag Chemie, 4. Aufl. 1966
Bemerkungen
(1)
Die Herleitung wurde im Seminar zum Praktikum im einzelnen durchgeführt.
(2)
Das chemische Potenzial einer Spezies in einem isothermen, isobaren System ist die partielle molare Freie Enthalpie dieser Spezies. Bitte rekapitulieren Sie den Begriff "partielle molare Größe".
(3)
Der Zusammenhang zwischen der Differenz μB - μA der chemischen Potentiale μA und μB und der
Freien Reaktionsenthalpie ΔG einer Reaktion A  B wurde in der Grundvorlesung im WS 2006/2007 ausführlich hergeleitet; der Zusammenhang lautet ΔG = μB - μA.