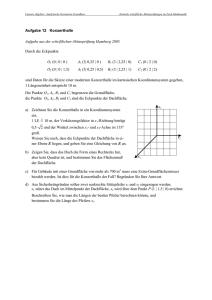
Aufgabe B1 – Nachtermin 2013

Hessisches Kultusministerium
Landesabitur 2013 (Nachtermin)
Mathematik
Grundkurs (TR / GTR / CAS)
Thema und Aufgabenstellung
Vorschlag B1
Lineare Algebra / Analytische Geometrie
Aufgaben
Eine junge Familie plant ein Haus zu bauen. Mit ihrem Architekten möchte sie einen Bauplan erstellen,
der auch mit Hilfe eines Computerprogramms dreidimensional veranschaulicht werden kann. Hierzu
wird der Plan in ein dreidimensionales Koordinatensystem überführt.
Das Gebäude (mit Dach) soll am Boden durch die Punkte A(0|0|0), B(10|0|0), C(10|8|0) und
D(0|8|0) begrenzt werden. Bis zum Dachboden (Deckenabschluss des obersten Stockwerks) soll die
Höhe 8 Meter betragen.
Der Dachfirst (obere Dachkante) wird durch die Punkte K1(3|4|12) und K2(7|4|12) begrenzt.
Alle Koordinaten sind in der Einheit Meter angegeben.
Die y-Achse des Koordinatensystems zeigt nach Osten.
1.
Zeichnen Sie durch Ergänzen des Materials ein Schrägbild des Gebäudes. Bezeichnen Sie den
noch nicht benannten Eckpunkt mit E und geben Sie die Koordinaten von E, F, G und H an.
(6 BE)
2.
Um die Kosten für das Eindecken des Daches abschätzen zu können, soll die gesamte Dachfläche
des Hauses bestimmt werden. Dabei wurden die Flächen der Nord- und Südseite des Dachs bereits bestimmt. Sie betragen zusammen 40m2.
Berechnen Sie den Inhalt der gesamten Dachfläche.
(Dachüberstände über die Hauswände sollen hierbei nicht berücksichtigt werden.)
(7 BE)
3.
Nach den Bebauungsplänen der Gemeinde darf die Dachneigung des Hauses (Winkel zwischen
Dachfläche und der Horizontalen) einen maximalen Wert nicht überschreiten.
Bestimmen Sie einen Vektor, der senkrecht auf der südlichen Dachfläche steht, und erklären
Sie, wie man damit den Neigungswinkel der Dachfläche berechnen kann. Die Berechnung der
Größe des Winkels ist nicht erforderlich.
(9 BE)
4.
Die Familie möchte den Dachboden eventuell auch als Wohnraum nutzen und fragt sich, ob dies
wegen der Dachschrägen überhaupt möglich ist.
Untersuchen Sie, ob eine erwachsene Person von 1,75m Größe am Punkt X(4|6|8) noch aufrecht stehen kann. Die Dicke des Daches soll dabei unberücksichtigt bleiben.
(8 BE)
Seite 2 von 3
Hessisches Kultusministerium
Landesabitur 2013 (Nachtermin)
Mathematik
Grundkurs (TR / GTR / CAS)
Thema und Aufgabenstellung
Vorschlag B1
Material
Seite 3 von 3
Landesabitur 2013 (Nachtermin)
Mathematik
Grundkurs (TR / GTR / CAS)
Lösungs- und Bewertungshinweise
Vorschlag B1
I.
Erläuterungen
Voraussetzungen gemäß Lehrplan und Erlass „Hinweise zur Vorbereitung auf die schriftlichen
Abiturprüfungen im Landesabitur 2013“ vom 20. Juni 2011
Q2 Lineare Algebra / Analytische Geometrie
Lagebeziehungen von Punkten, Geraden und Ebenen im Raum, Flächenberechnung, Orthogonalität,
Abstandsbestimmung
II. Lösungshinweise und Bewertungsraster
In den nachfolgenden Lösungshinweisen sind alle wesentlichen Gesichtspunkte, die bei der Bearbeitung der einzelnen Aufgaben zu berücksichtigen sind, konkret genannt und diejenigen Lösungswege
aufgezeigt, welche die Prüflinge erfahrungsgemäß einschlagen werden. Selbstverständlich sind jedoch
Lösungswege, die von den vorgegebenen abweichen, aber als gleichwertig betrachtet werden können,
ebenso zu akzeptieren.
Aufg. erwartete Leistungen
1
E(0|0|8), F(10|0|8), G(10|8|8), H(0|8|8)
BE
I
II III
2
2
2
Seite 1 von 3
Nicht für den Prüfling bestimmt
Hessisches Kultusministerium
Landesabitur 2013 (Nachtermin)
Mathematik
Grundkurs (TR / GTR / CAS)
Lösungs- und Bewertungshinweise
Vorschlag B1
BE
Aufg. erwartete Leistungen
2
Die fehlenden Dachflächen GHK1K2 und EFK2K1 sind kongruente Trapeze.


Für das Trapez GHK1K2 gilt: GH = 10 (m) und K1K 2 = 4 (m).

Höhe h im Trapez GHK1K2: K1P mit P(3|8|8), also h = 42  42  4  2 (m)
1  
ATrapez =  GH  K1K 2  h  28  2 m²  39,6 m²
2
Ages = 40 m²  2  28  2 m²  119, 2 m²
Die gesamte Dachfläche beträgt ungefähr 119,2m2.

3
I
II III
2
5
3
3

Die südliche Dachfläche ist das Dreieck FGK2.
0
 3 
   
   
Mögl. Richtungsvektoren der Ebene E FGK 2 : u  FG =  8  und v  FK 2 =  4 
0
4
 
 



Bestimme einen Normalenvektor n , der auf u und v jeweils senkrecht steht.
0
  
n   8   8  n 2  0 , also n2 = 0
0
 
 3 
  
3
n   4   3  n1  4  n 2  4  n 3  3  n1  4  n 3  0 , also n 3   n1
4
4
 
 4
  
Für n1= 4 ist dann n3 = 3, somit ist n   0  ein Vektor, der senkrecht auf der
 3
 
südlichen Dachfläche steht.

Der Winkel  zwischen dem Normalenvektor n der Ebene E FGK 2 und dem Nor
malenvektor e3 der x-y-Ebene ist gleich dem Neigungswinkel der Ebene E FGK 2 .
Dachfläche
α
α
 
n  e3
Winkelberechnung durch cos()   
n  e3
3
Seite 2 von 3
Nicht für den Prüfling bestimmt
Hessisches Kultusministerium
Landesabitur 2013 (Nachtermin)
Mathematik
Grundkurs (TR / GTR / CAS)
Lösungs- und Bewertungshinweise
Vorschlag B1
BE
Aufg. erwartete Leistungen
4
I
II III
Die in dieser Aufgabe zu betrachtende Dachfläche ist GHK1K2 in der Ebene
E GHK1K 2 .
Mögliche Ebenengleichung:
 10 
 10 
 3 
  


 
E GHK1K 2 : x   8   r   0   s   4  , r, s IR
8
 0 
 4
 


 
2
Berechnung des Schnittpunkts X einer zur z-Achse parallelen Geraden mit dem
 0  10   10   3 
 4  4
    
    
  
Stützvektor x   6  :  6   t   0    8   r  0   s  4 
1  8   0   4 
8 8
    
  
   
Lösung: s =
1
9
, t = 2 und r =
2
20
2
Der Punkt X'(4|6|10) liegt 2m über dem Punkt X(4|6|8), die Person könnte
daher am Punkt X noch aufrecht stehen.
3
1
Summe 30 9
15
6
III. Bewertung und Beurteilung
Die Bewertung und Beurteilung erfolgt gemäß den Bestimmungen in der OAVO in der jeweils gültigen Fassung, insbesondere §33 OAVO in Verbindung mit den Anlagen 9a und ggf. 9b bis 9f, sowie in
den Einheitlichen Prüfungsanforderungen in der Abiturprüfung (EPA). Für die Umrechnung von Prozentanteilen der erbrachten Leistungen in Notenpunkte nach §9 Abs. 12 der OAVO gelten die Werte
in der Anlage 9a der OAVO. Darüber hinaus sind die Vorgaben des Erlasses „Hinweise zur Vorbereitung auf die schriftlichen Abiturprüfungen im Landesabitur 2013“ vom 20. Juni 2011 zu beachten.
Im Fach Mathematik besteht die Prüfungsleistung aus der Bearbeitung je eines Vorschlags aus den Bereichen Analysis, lineare Algebra und Stochastik, wofür insgesamt maximal 100 BE vergeben werden
können. Ein Prüfungsergebnis von 5 Punkten (ausreichend) setzt voraus, dass insgesamt 46 BE, ein
Prüfungsergebnis von 11 Punkten (gut), dass insgesamt 76 BE erreicht werden.
Gewichtung der Aufgaben und Zuordnung der Bewertungseinheiten zu den Anforderungsbereichen
Aufgabe
1
2
3
4
Summe
Bewertungseinheiten in den Anforderungsbereichen
AFB I
AFB II
AFB III
4
2
2
5
3
3
3
5
3
9
15
6
Summe
6
7
9
8
30
Die auf die Anforderungsbereiche verteilten Bewertungseinheiten innerhalb der Aufgaben sind als
Richtwerte zu verstehen.
Seite 3 von 3
Nicht für den Prüfling bestimmt
Hessisches Kultusministerium