Schriftliche Abiturprüfung Sachsen – Anhalt 2016 EAN Thema G 1
Werbung
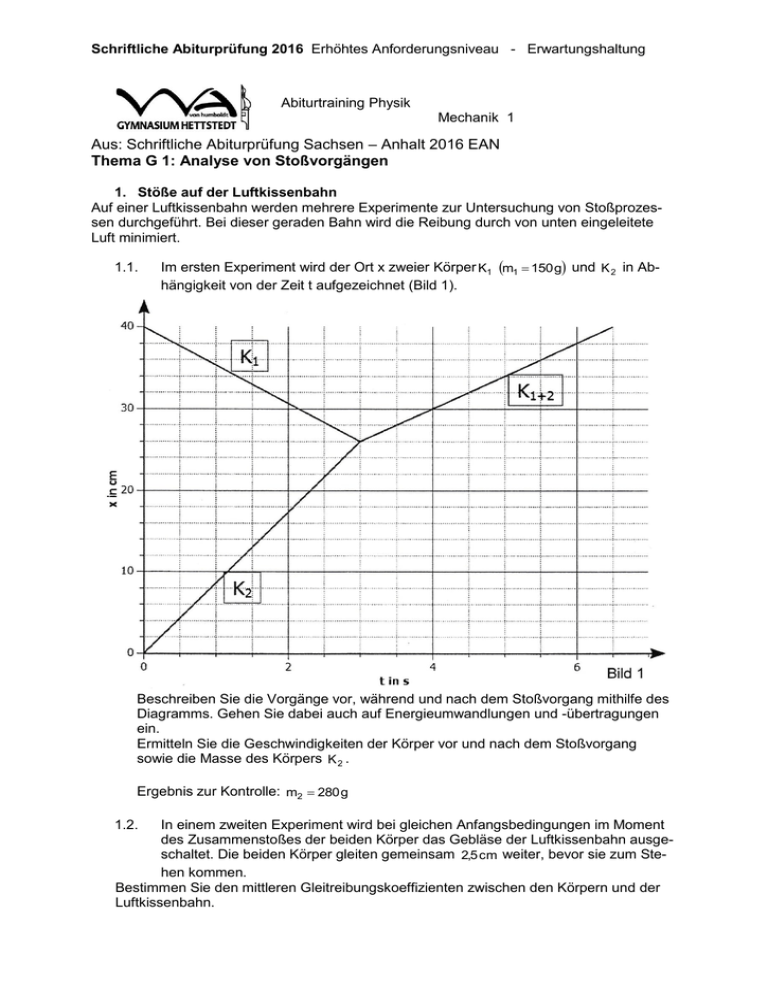
Schriftliche Abiturprüfung 2016 Erhöhtes Anforderungsniveau - Erwartungshaltung Abiturtraining Physik Mechanik 1 Aus: Schriftliche Abiturprüfung Sachsen – Anhalt 2016 EAN Thema G 1: Analyse von Stoßvorgängen 1. Stöße auf der Luftkissenbahn Auf einer Luftkissenbahn werden mehrere Experimente zur Untersuchung von Stoßprozessen durchgeführt. Bei dieser geraden Bahn wird die Reibung durch von unten eingeleitete Luft minimiert. 1.1. Im ersten Experiment wird der Ort x zweier Körper K1 m1 150 g und K 2 in Abhängigkeit von der Zeit t aufgezeichnet (Bild 1). Beschreiben Sie die Vorgänge vor, während und nach dem Stoßvorgang mithilfe des Diagramms. Gehen Sie dabei auch auf Energieumwandlungen und -übertragungen ein. Ermitteln Sie die Geschwindigkeiten der Körper vor und nach dem Stoßvorgang sowie die Masse des Körpers K 2 . Ergebnis zur Kontrolle: m2 280 g 1.2. In einem zweiten Experiment wird bei gleichen Anfangsbedingungen im Moment des Zusammenstoßes der beiden Körper das Gebläse der Luftkissenbahn ausgeschaltet. Die beiden Körper gleiten gemeinsam 2,5 cm weiter, bevor sie zum Stehen kommen. Bestimmen Sie den mittleren Gleitreibungskoeffizienten zwischen den Körpern und der Luftkissenbahn. Schriftliche Abiturprüfung 2016 Erhöhtes Anforderungsniveau - Erwartungshaltung 1.3. In einem dritten Experiment wird bei wieder eingeschaltetem Gebläse und gleichen Anfangsbedingungen der Stoß vollkommen elastisch durchgeführt. Stellen Sie den Vorgang in einem x(t) - Diagramm im Arbeitsblatt 1 (Seite 12) dar und fügen Sie dieses Ihren Unterlagen bei. 2. Stöße beim Tennisspiel Ein Tennisspieler schlägt einen auf ihn zukommenden Ball m 56 g zurück. Die Geschwindigkeit des Massenmittelpunktes des Balls ist in folgendem Diagramm idealisiert festgehalten. 2.1. Beschreiben Sie die Bewegung des Balls mithilfe des Diagramms (Bild 2). 2.2. Ermitteln Sie aus dem Diagramm (Bild 2) näherungsweise die mittlere und die maximale Kraft, die auf den Ball wirkt. Beschreiben Sie Ihr Vorgehen. 2.3. Mithilfe eines Modellexperiments wird die Dehnung der Bespannung des Schlägers sowie die maximalwirkende Kraft bestimmt. Für die auf den Schläger wirkende Kraft gilt folgender Zusammenhang: F s k s3 . Bestimmen Sie die Konstante k, wenn die maximale Kraft von F 1000N bei einer Dehnung von s 2,0 cm wirkt. Berechnen Sie die Federspannarbeit für diesen Vorgang. Schriftliche Abiturprüfung 2016 Erhöhtes Anforderungsniveau - Erwartungshaltung 3. Rutherford´scher Streuversuch Rutherford untersuchte Anfang des 20. Jahrhunderts das Verhalten von Alphateilchen (Heliumkerne), die auf eine äußerst dünne Goldfolie gestrahlt wurden (Bild 3). Die Austrittsgeschwindigkeit der Alphateilchen aus dem Strahler betrug dabei ca. 2 107 m s1 . Er machte folgende Beobachtungen: a) Die überwiegende Anzahl der Teilchen durchdringt die Folie ungehindert. b) Ein kleiner Teil der Teilchen wird um wenige Grad abgelenkt. c) Nur einige Teilchen werden um einen Winkel über 90" abgelenkt. 3.1. 3.2. 3.3. Erläutern Sie, welche Schlussfolgerungen Rutherford aus diesen Beobachtungen bezüglich des Aufbaus von Atomen gezogen hat. Beschreiben Sie, worin die Grenzen des Rutherford'schen Atommodells aus heutiger Sicht liegen. Berechnen Sie die Coulombkraft, die zwischen einem Alphateilchen und einem Atomkern des Goldes wirkt, wenn diese sich in einem Abstand von 1,44 1010 m befinden. Das Zurückwerfen der Alphateilchen zur Quelle kann als zentraler elastischer Stoß betrachtet werden. Berechnen Sie die theoretischen Geschwindigkeiten eines Alphateilchens und eines ruhenden freien Goldkerns nach dem Stoß. Diskutieren Sie, welche Auswirkungen die Bindung des Goldkerns im Metallgitter auf seine Geschwindigkeit nach dem Stoß haben könnte. Schriftliche Abiturprüfung 2016 Erhöhtes Anforderungsniveau - Erwartungshaltung Abiturtraining Physik Mechanik 1 Thema G 1: Analyse von Stoßvorgängen 1. Stöße auf der Luftkissenbahn Auf einer Luftkissenbahn werden mehrere Experimente zur Untersuchung von Stoßprozessen durchgeführt. Bei dieser geraden Bahn wird die Reibung durch von unten eingeleitete Luft minimiert. 1.1. m2 = 278,57g 280 g 1.2. 0,00326 3.3 10-3 1.3. x(t) – Diagramm 2. Stöße beim Tennisspiel 2.1. 2.2. Mittlere Kraft auf den Ball F 630 N Maximale Kraft Fmax m amax 1562,78N 1600 N Berechnung der maximal auftretenden Beschleunigung und der maximal auftretenden Kraft mithilfe der Wendetangenten: Schriftliche Abiturprüfung 2016 Erhöhtes Anforderungsniveau - Erwartungshaltung 2.3. Berechnung von k: F s k s3 Berechnung der Federspannarbeit s1 WFeder Fs ds s0 k s ds s1 3 s0 WFeder 5 Nm 5 J 3. Rutherford´scher Streuversuch 3.1. FC 1,76 10-6 N 3.2. 3.3. uAu u2 7,96 105 m s k 125 106 N m3