Obersumme Untersumme Zwischenwertsumme

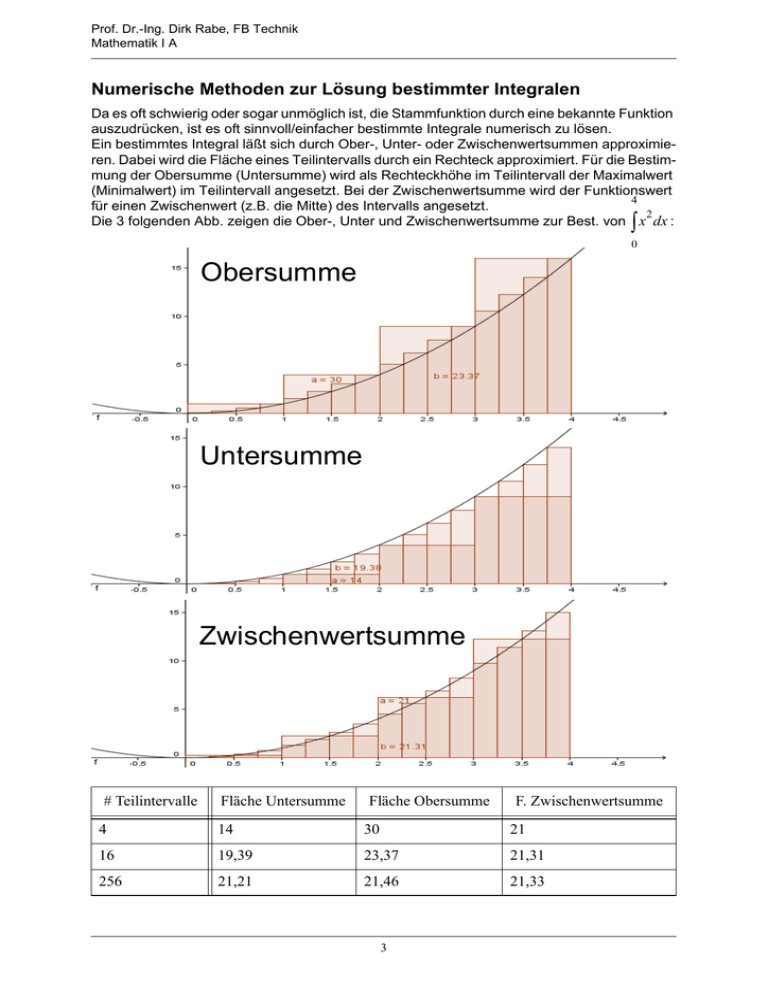
Prof. Dr.-Ing. Dirk Rabe, FB Technik
Mathematik I A
Numerische Methoden zur Lösung bestimmter Integralen
Da es oft schwierig oder sogar unmöglich ist, die Stammfunktion durch eine bekannte Funktion
auszudrücken, ist es oft sinnvoll/einfacher bestimmte Integrale numerisch zu lösen.
Ein bestimmtes Integral läßt sich durch Ober-, Unter- oder Zwischenwertsummen approximieren. Dabei wird die Fläche eines Teilintervalls durch ein Rechteck approximiert. Für die Bestimmung der Obersumme (Untersumme) wird als Rechteckhöhe im Teilintervall der Maximalwert
(Minimalwert) im Teilintervall angesetzt. Bei der Zwischenwertsumme wird der Funktionswert
4
für einen Zwischenwert (z.B. die Mitte) des Intervalls angesetzt.
2
Die 3 folgenden Abb. zeigen die Ober-, Unter und Zwischenwertsumme zur Best. von x dx :
∫
0
Obersumme
Untersumme
Zwischenwertsumme
# Teilintervalle
Fläche Untersumme
Fläche Obersumme
F. Zwischenwertsumme
4
14
30
21
16
19,39
23,37
21,31
256
21,21
21,46
21,33
3
Prof. Dr.-Ing. Dirk Rabe, FB Technik
Mathematik I A
Die exakte mathematische Lösung für dieses Beispiel ist natürlich sehr einfach:
4
3 4
x
2
∫ x dx = ----3-
0
64
1
= ------ = 21 --3
3
0
Der Grenzwert für #Teilintervalle → ∞ strebt für alle 3 Summen gegen den Wert des tatsächlichen bestimmten Integrals:
4
∫x
n
2
dx = lim
n→∞
0
n
∑
n
4–0
4–0
4–0
U i ⋅ ------------ = lim ∑ O i ⋅ ------------ = lim ∑ Z i ⋅ -----------n
n
n
n→∞
n→∞
i=1
i=1
i=1
Neben diesen 3 Verfahren gibt es folgende weitere Verfahren:
• Links- und Rechtssumme: ähnlich Unter-/Obersumme; jedoch wird anstelle des Max-/MinWertes immer der linke bzw. rechte Funktionswert angesetzt - für obiges Beispiel entspricht
die Untersumme auch der Linkssumme und die Rechtssumme der Obersumme, da die Beispielfunktion im Integrations-Intervall monoton steigt.
• Trapezsumme: Die Fläche für das Intervall [xi;xi+1] wird durch ein Trapez angenähert. Die
f( x
) + f(x )
i–1
i
Teilfläche von einem Trapez ist gegeben durch A i = ----------------------------------- ⋅ ( x i + 1 – x i )
2
• Simpson-Summe:
Beim Trapezsummen-Verfahren wird die Funktionskurve für ein Teilintervall durch seine Sekante angenähert.
Bei der Simpson-Summe wird die Funktionskurve durch ein Polynom 2.Grades
2
( y = a 2 x + a 1 x + a 0 ) für einen Doppelstreifen angenähert (siehe Abbildung). D.h., dass
das Polynom durch die 3 Kurvenpunkte P0, P1 und P2 von f(x) definiert ist. Der Flächeninhalt
AP1 zwischen dem Polynom und der x-Achse soll also den Flächeninhalt zwischen f(x) und
der x-Achse im Intervall [x0,x2] approximieren.
y
P2
f(x)
P1
y1
P0
y0
x0
h
y2
h
x
x1
4
x2
Prof. Dr.-Ing. Dirk Rabe, FB Technik
Mathematik I A
Der Flächeninhalt AP1 läßt sich wie folgt berechnen:
x + 2h
A P1 =
∫
x0
3
2
a1 x
⎛ a2 x
⎞
2
( a 2 x + a 1 x + a 0 ) dx = ⎜ ---------- + ---------- + a 0 x⎟
2
⎝ 3
⎠
3
x 0 + 2h
x0
3
2
2
a 1 ( x 0 + 2h )
a2 x0 a1 x0
a 2 ( x 0 + 2h )
= ------------------------------- + ------------------------------- + a 0 ( x 0 + 2h ) – ------------- – ------------- – a 0 x 0
3
2
3
2
3
=
2
a2 x0
a1 x0
2
------------ + 2a 2 x 20 h + 4a 2 x 0 h 2 + 8--- a 2 h 3 + ---------+ 2a 1 x 0 h + 2a 1 h + a 0 x 0 + 2a 0 h
3
2
3
3
2
a2 x0 a1 x0
– ------------- – ------------- – a 0 x 0
3
2
2 8
3
2
2
= 2a 2 x 0 h + 4a 2 x 0 h + --- a 2 h + 2a 1 x 0 h + 2a 1 h + 2a 0 h
3
h
2
2
= --- ( 6a 2 x 0 + 12a 2 x 0 h + 8a 2 h + 6a 1 x 0 + 6a 1 h + 6a 0 )
3
⎧
⎪
⎪
⎨
⎪
⎪
⎩
2
⎛
h--- ⎜ a 2 x 0 + a 1 x 0 + a 0
3⎜
y0
⎝
2
2
=
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
⎛ a 2 x 0 + 2a 2 x 0 h + a 2 h
⎞
⎜
+ a 1 ( x 0 + h ) + a 0⎟
⎜
⎟
2
+4 ⎝
⎠
a2 ( x0 + h )
y1
2
2
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
a 2 x 0 + 4a 2 x 0 h + 4a 2 h
a 2 ( x 0 + 2h )
2
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
+
⎞
⎟
+ a 1 ( x 0 + 2h ) + a 0 ⎟
⎟
⎟
⎟
⎠
y2
h
A P1 = --- ( y 0 + 4y 1 + y 2 )
3
Daraus folgt, dass man die Koeffizienten a2, a1 und a0 nicht bestimmen muss, um die Fläche AP1 zu bestimmen. Analog zur Berechnung des Flächeninhalts AP1 können die Flächeninhalte der Doppelstreifen APi berechnet werden:
h
h
A P2 = --- ( y 2 + 4y 3 + y 4 )
A P3 = --- ( y 4 + 4y 5 + y 6 )
3
3
h
A Pi = --- ( y 2i – 2 + 4y 2i – 1 + y 2i )
3
b
Das zu approximierende bestimmte Integral I =
∫ f ( x ) dx soll nun durch die Aufsummiea
rung von n Doppelstreifen gebildet werden. Hierbei fällt auf, dass alle ungeraden Stützstel-
5
Prof. Dr.-Ing. Dirk Rabe, FB Technik
Mathematik I A
len 4-fach in die Flächenbildung eingehen und alle geraden Stützstellen bei zwei
aufeinanderfolgenden Doppelstreifen je 1x (also insgesamt 2x) berücksichtigt werden (Ausnahme erster und letzter Doppelstreifen). Das bestimmte Integral läßt sich also wie folgt
approximieren:
b
I =
n
∫ f ( x ) dx ≈ ∑
i=1
A Pi
a
i=1
( y 1 + y 3 + … + y 2n – 1 ) ⎞
⎛
⎟ + 2⎜
⎠
⎝
S1
( y 2 + y 4 + … + y 2n – 2 ) ⎞ ⎞
⎟⎟
⎠⎠
S2
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
⎛
+ 4⎜
⎝
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
∑ APi
h--- ⎛ y 0 + y 2n
= ⎜
3⎝
S0
⎧
⎪
⎨
⎪
⎩
n
Sämtliche dieser Approximationsverfahren konvergieren für n → ∞ gegen den tatsächlichen
Integralwert. Erfahrungsgemäß konvergieren die verschiedenen Vefahren in folgender Reihenfolge:
• am schnellsten: Simpson-Summe
• Zwischenwertsumme
• Trapezsumme
• Unter-, Ober-, Links- und Rechtssumme
6
Prof. Dr.-Ing. Dirk Rabe, FB Technik
Mathematik I A
Lösung komplizierter unbestimmter Integrale
Trignometrische Integrale
Enthalten die Integranden Produkte mehrerer trigonometrischer Funktionen oder zusammengesetzte Funktionen mit trigonometrischen Funktionen, so kann man diese oft durch geschickte Umformungen und Substitutionen lösen.
∫
∫ ( sin x )
3
Beispiele: ( cos x ) dx
5
2
( cos x ) dx
Wichtige trigonometrische Beziehungen für Umformungen:
2
sin ϕ
tan ϕ = -----------cos ϕ
2
( sin ϕ ) + ( cos ϕ ) = 1
1
2
1 + ( tan ϕ ) = -------------------2
( cos ϕ )
1
sin α ⋅ cos β = --- [ sin ( α – β ) + sin ( α + β ) ]
2
1
sin α ⋅ sin β = --- [ cos ( α – β ) – cos ( α + β ) ]
2
1
cos α ⋅ cos β = --- [ cos ( α – β ) + cos ( α + β ) ]
2
1 + cos 2ϕ
2
( cos ϕ ) = ------------------------2
3 cos ϕ + cos 3ϕ
3
( cos ϕ ) = -------------------------------------4
sin nϕ =
cos n ϕ =
n
n
n
n
1 – cos 2ϕ
2
( sin ϕ ) = -----------------------2
3 sin ϕ – sin 3 ϕ
3
( sin ϕ ) = ----------------------------------4
∑k = 0 ⎛⎝ k⎞⎠ ( cos ϕ ) ( sin ϕ )
k
∑k = 0 ⎛⎝ k⎞⎠ ( cos ϕ ) ( sin ϕ )
k
n–k
n–k
sin ⎛ ----------- π⎞
⎝ 2 ⎠
n–k
n–k
cos ⎛ ----------- π⎞
⎝ 2 ⎠
n!
⎛ n⎞ = -------------------------⎝ k⎠
( n – k )! ⋅ k!
n! = n ⋅ ( n – 1 ) ⋅ ( n – 2 )…3 ⋅ 2 ⋅ 1
1 – cos 4ϕ
2
2
( sin ϕ ) ( cos ϕ ) = -----------------------8
0! = 1
3
( sin 2ϕ )
3
3
( sin ϕ ) ( cos ϕ ) = ---------------------8
Weitere Strategien werden in der Vorlesung behandelt.
7
Prof. Dr.-Ing. Dirk Rabe, FB Technik
Mathematik I A
Trigonometrische Grundintegrale
f( x)
F(x) =
∫ f ( x ) dx
f(x)
F(x) =
∫ f ( x ) dx
cos x
sin x + C
tan x
1 - +C
ln ---------cos x
sin x
– cos x + C
cot x
ln sin x + C
1
-----------------2
( cos x )
tan x + C
1--------sin x
1
ln ---------- + cot x + C
sin x
1
----------------2
( sin x )
1
– ---------- + C = – cot x + C
tan x
1---------cos x
1
ln ----------- + tan x + C
cos x
sin x
-----------------2
( cos x )
1---------+C
cos x
cos x
----------------2
( sin x )
1
– ---------- + C
sin x
Trignometrische Substitution
Für folgende Terme im Integranden bieten sich trigonometrische Funktionen zur Substitution
an:
Term im
Integranden
2
2
2
2
2
2
a –x
a +x
x –a
Substitution
Definitionsbereich
von ϕ
trignometrische
Beziehung zur
Vereinfachung
x = a ⋅ sin ϕ
dx = a ⋅ cos ϕ ⋅ dϕ
π
π
– --- ≤ ϕ ≤ --2
2
1 – ( sin ϕ ) = ( cos ϕ )
x = a ⋅ tan ϕ
a
dx = -------------------2 ⋅ dϕ
( cos ϕ )
π
π
– --- < ϕ < --2
2
1
2
1 + ( tan ϕ ) = -------------------2
( cos ϕ )
a
x = -----------cos ϕ
tan ϕ
dx = a ⋅ ------------ ⋅ dϕ
cos ϕ
π
0 ≤ ϕ < --- oder
2
π
--- < ϕ ≤ π
2
1
2
------------------–
1
=
(
tan
ϕ
)
2
( cos ϕ )
8
2
2
Prof. Dr.-Ing. Dirk Rabe, FB Technik
Mathematik I A
graphische Darstellung der o.a. Integranden:
2
x –4
4+x
2
4–x
2
9