Lehrveranstaltung "Grundlagen der Elektronik"

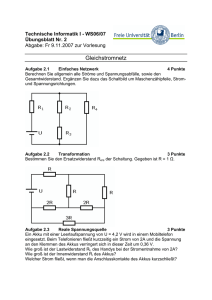
Lehrveranstaltung "Grundlagen
der Elektronik"
Stand: Ecke, 28.04.14
Übungsaufgaben
1.
Zur Wiederholung der Stromkreisberechnung mit den Kirchhoffschen Gesetzen
bei linearen aktiven Zweipolen und des Satzes von Helmholtz lösen Sie die folgenden Aufgaben:
Ein elektronisches Gerät hat bei einer Betriebsspannung UL = 9 V eine Stromaufnahme IL = 20 mA. Dieses Gerät soll an ein Gleichspannungsnetzgerät mit
einer Leerlaufspannung Uq von 150 V und einem Innenwiderstand Ri = 200 Ω
angeschlossen werden. Zur Herabsetzung der Spannung ist ein ohmscher Spannungsteiler aus zwei Festwiderständen zu verwenden.
Berechnen Sie
a)
den Widerstandswert und die Verlustleistung für den Längswiderstand
R1 unter Anwendung der Kirchhoffschen Gesetze, wenn der Querwiderstand R2 parallel zum Verbraucher einen Wert von 180 Ω hat.
b)
die Stromaufnahme und Betriebsspannung desselben Gerätes (lineare
Abhängigkeit IL = f(UL) vorausgesetzt), wenn dem angegebenen Gleichspannungsnetzgerät ein Spannungsteiler mit den Widerstandswerten R1 =
1 kΩ, R2 =150 Ω vorgeschaltet wird. Für das Gleichspannungsnetzgerät
und den Spannungsteiler zeichnen und berechnen Sie eine Spannungsquellen-Ersatzschaltung.
c)
die Änderung der Betriebsspannung des Gerätes ΔUL bei einer Änderung
der Leerlaufspannung des Gleichspannungsnetzgerätes um ΔUq = ± 15 V
bei Verwendung des Spannungsteilers nach Aufgabe b).
2.
Gegeben ist folgende Schaltung:
Uq = 9 V,
R1 = 330 Ω, R2 = 220 Ω,
R3 = 330 Ω, R4 = 100 Ω,
R5 = 470 Ω, R6 = 220 Ω.
Berechnen Sie Strom und Spannung am Widerstand R4! (Leiten Sie zuvor die Transformation für Widerstände von Dreieck- in
Sternschaltung her!)
3
Durch Anwendung der folgenden Schaltung mit einem Varistor parallel zum Verbraucherwiderstand RL lässt sich bei schwankender Betriebsspannung die Gleichspannung
am Verbraucher stabilisieren. Für die I-U-Kennlinie des Varistors gilt die folgende
Wertetabelle:
±U/V
± I / mA
0
0
14
5
18
10
21
20
23
30
27
50
32.5
100
35
150
Die Widerstände haben die Werte RV=1.5 kΩ und RL=1 kΩ.
Lösen Sie die Aufgaben a) bis c) grafisch.
a)
Welcher Gleichspannungswert stellt sich in
dieser Schaltung bei Uq=150 V ein?
Uq
b)
Wie groß sind dabei IV, IL und der Strom
durch den Varistor?
c)
Wie groß ist die Gleichspannungsänderung )UL am Lastwiderstand, wenn die
Änderung der Betriebsspannung )Uq = ±25 V beträgt?
d)
Bei einer Spannungsquelle von Uq=150 V, einem Lastwiderstand von RL=1 kΩ
und einem unbekannten Vorwiderstand wird eine Ausgangsspannung von UL =
30 V gemessen. Wie groß ist der unbekannte Vorwiderstand RV.
4.
In einem Kubikzentimeter Kupfer befinden sich cirka 10²² freie Elektronen, in
Si einer bestimmten Dotierung (Substrat eines TTL-Schaltkreises) 5 · 1014 freie
Elektronen. Wird an ein 1 m langes Stück Cu bzw. Si mit einem Querschnitt
von 1 mm2 eine Spannung von 0,1 V angelegt, dann fließen im Kupfer 5.88 A,
im Silizium 1 µA.
a)
Wie groß ist der spezifische Widerstand des Cu und des Si?
b)
Wie groß ist die Elektronengeschwindigkeit im Cu bzw. Si?
c)
Wie groß sind die Beweglichkeiten µ (Geschwindigkeit bezogen auf die
Feldstärke)?
d)
Welche Verlustleistung wird im Cu bzw. im Si umgesetzt?
e)
Auf welchen Wert ändert sich der Widerstand des Kupferdrahtes bei einer Temperaturerhöhung um 50 K (Temperaturkoeffizient:
TK = 3.9 · 10-3 K-1)?
5.
a) Wie groß ist der Temperaturkoeffizient TK der Eigenleitungsdichte ni in Si
bei T = 300 K?
Eigenleitungsdichte
ni(T0 = 300 K) = 1,5·1010 cm-3,
Breite der verbotenen Zone
Wg = 1,1 eV,
thermische Energie bei T0 = 300 K: kT0 = 0,025 eV.
b) Berechnen Sie die Änderung von ni bei einer Temperaturerhöhung um 20 K
einmal exakt mittels der Formel für ni und zum anderen durch Anwendung
des TK. Wie groß ist der Fehler?
6.
In integrierten Schaltkreisen sind Widerstände 2 bis 5 µm dicke Si-Bahnen, die
durch so genannte Sperrschichten von dem sie umgebenden Si isoliert sind, mit
etwa 1017 Elektronen pro cm3 (ρ = 0,05 Ωcm).
a)
Wie groß ist der Widerstand eines Bahnstückes von gleicher Länge L
und Breite W bei einer Dicke H = 5 µm, der so genannte Flächenwiderstand RS?
b)
Wie lang wird ein 10 kΩ Widerstand, wenn er 10 µm breit gemacht werden kann?
Welche Fläche nimmt er ein, wenn er durch Mäanderform etwa quadratisch gemacht wird (Bahnabstand 10 µm) und wie viele solcher Widerstände passen auf einen Quadratmillimeter, wenn zur gegenseitigen Isolation etwa 30 µm Abstand zwischen den Widerstandsfeldern vorzusehen ist?
Wie hoch ist der Löcheranteil an der Leitfähigkeit?
(ni = 1,5·1010 cm-3, µn = 1250 cm2/Vs, µp = 480 cm2/Vs,)
c)
d)
7.
Ein Elektrolytkondensator habe 100 µF.
a) Wie groß ist die Elektrodenfläche (εr = 10; dOX = 50nm)?
b) Welche Fläche müsste ein "Luft" - Kondensator gleicher Kapazität bei einem
Elektrodenabstand von 0,1 mm haben (ε0 = 8,859·10-12 As/Vm)?
8.
Für einen Widerstand sind folgende Werte bekannt:
R = 4,7 kΩ, P70 = 2 W (max. el. Leistung bei einer Umgebungstemperatur von
max. 70 °C), maximale Schichttemperatur 140 °C
Bis zu welcher Spannung darf der Widerstand bei 40 °C und 100 °C Umgebungstemperatur betrieben werden?
9.
An einem realer Kondensator, beschrieben durch die nebenstehende Ersatzschaltung (R1=2 Ω, R2= 25kΩ, C=35µF), liegt eine Wechselspannung von 10V
effektiv mit einer Frequenz von 50 Hz an.
a) Berechnen Sie den komplexen Widerstand der Schaltung!
b) Wie groß sind Schein-, Blind- und
Wirkleistung dieser Schaltung? Diskutieren Sie die Ergebnisse im Vergleich
zum idealen Fall!
10.
Gegeben sind die beiden Schaltungen mit R= 4,7kΩ und C=3,3nF:
(1)
a)
(2)
Bestimmen Sie die komplexe Übertragungsfunktion!
b)
Zeichen Sie die Verläufe der Amplitude (logarithmischer Maßstab) und
der Phase als Funktion der Frequenz (logarithmischer Maßstab) im Bereich von 10Hz bis 10MHz. Charakterisieren sie die beiden Schaltungen!
c) Berechnen Sie die Grenzfrequenz!
11.
Eine Gleichspannung mit überlagerter Wechselspannung soll "gesiebt" werden.
Dazu wird eine L-C-Kombination verwendet.
Folgende Werte sind gegeben:
C
= 100 µF,
f
= 50 Hz,
Verlustwinkel der Spule:
tan δ = 10-2 (Drossel),
a)
b)
c)
12.
Wie sieht die Schaltung aus?
Welchen Wert muss die Induktivität haben, damit die Amplitude der
Wechselspannung auf 10 % abfällt?
Wie groß darf der Wicklungswiderstand der Drossel sein?
Ein idealer Transformator mit 2 Sekundärwicklungen wird mit einer Primäreffektivspannung von 24V betrieben. Die Primärwicklung hat 900 Windungen
und die 1. Sekundärwicklung 300.
a)
Wie viele Windungen muss die 2. Sekundärwicklung haben, damit eine
Effektivspannung von 2,5 V bereitgestellt wird?
b)
Wie groß ist der Primärstrom, wenn an den Klemmen der 1. Sekundärwicklung ein Widerstand von 200 Ω und an denen der 2. ein Widerstand
von 100 Ω angeschlossen werden?
13. Ein elektromagnetischer Schwingkreis, bestehend aus einer Spule mit einem Eisenkern der Induktivität von L=0.28H und einem Kondensator einer unbekannten
Kapazität schwingt ungedämpft mit der Eigenfrequenz f0. Die Frequenz der
Schwingung ist in einem Lautsprecher zu hören. Sie soll der Frequenz des Kammertons a mit 440 Hz entsprechen.
a)
Berechnen Sie den Wert des Kondensators!
b)
Entfernt man den Eisenkern aus der Spule, dessen Permeabilität
µr =1000 ist, so ändert sich die Induktivität der Spule. Berechnen Sie die
Tonhöhe (Frequenz) des Tones, der jetzt erklingt! Kann man diesen Ton
noch hören?
c)
Die Spule besteht aus einem Kupferdraht mit einem Widerstand von
RL=0.4 S. Wie hoch ist die Güte des Schwingkreises? Bei welchen Frequenzen ist die Amplitude der Schwingung (ohne Eisenkern) auf 70.7%
(3dB) abgefallen?
14.
Eine Si-Diode ist im n-Gebiet mit 1019 cm-3 Phosphoratomen dotiert. Das pSubstrat ist mit 3·1015 cm-3 Boratomen dotiert.
Silizium:
Eigenleitungsdichte
ni(T0 = 300 K) = 1,5·1010 cm-3,
Breite der verbotenen Zone
Wg = 1,1 eV,
Beweglichkeit der Elektronen
µn = 1250 cm2/Vs,
Beweglichkeit der Löcher
µp = 480 cm2/Vs,
thermische Energie der Ladungsträger bei T0 = 300 K: kT0 = 0,025 eV,
Elementarladung: e = 1,602·10-19 As.
a) Wie hoch sind die Elektronen- und Löcherkonzentrationen in den beiden
(homogen dotierten) Gebieten bei Raumtemperatur (T0 = 300 K) und bei
70 °C?
b) Berechnen Sie die Leitfähigkeiten beider Gebiete! Welchen Anteil haben
daran die Minoritätsladungsträger?
15.
a)
Berechnen Sie den Bahnwiderstand einer Halbleiterdiode (siehe Abb.)
zwischen pn-Übergang und Rückkontakt. Nehmen Sie pyramideförmigen
Stromfluss an (Integration).
Zeichnen Sie im linearen Maßstab die Diodenkennlinie (pn – Übergang
plus Bahnwiderstand) für den Bereich U= -2...1V (I = -5 ... 9 mA) auf,
wenn gilt:
U
pn
I = I S (e
nU T
− 1)
mit IS = 0,05 µA; n = 2; UT = 25 mV, :n = 1250 cm2/Vs.
b)
c)
d)
Ermitteln Sie grafisch Strom und Spannungen in einem Gleichstromkreis
mit dieser Diode, wenn R = 400 Ω und Uq = 2 V betragen.
Wie groß sind Strom und Spannung der Halbleiterdiode, wenn die Polarität der Quelle Uq geändert wird?
Um welchen Faktor erhöht sich der Strom in einer Halbleiterdiode bei einer Temperaturänderung von 300 K auf 320 K? Wie ändert sich die Diodenkennlinie (qualitativ)?
16.
Es steht die Netzspannung von Ueff=220V zur Verfügung. Ein Verbraucher soll
mit einer Gleichspannung von 12 V bei einer Stromaufnahme von 600 mA versorgt werden. Dazu ist ein Transformator mit einer Primärwicklung von 1800
Windungen vorhanden. Dimensionieren Sie die TransformatorSekundärwicklung und entwickeln Sie die Gleichrichterschaltung für a) eine
Einweg-Gleichrichtung und b) eine Zweiweggleichrichtung (Graetz-Brücke),
wenn die Welligkeit der Ausgangsspannung nicht größer als 5% betragen soll.
Für welche Sperrspannungen müssen die Dioden ausgelegt sein und wie spannungsfest muss der Elektrolytkondensator sein? Die Flussspannungen der Dioden sind bei der Dimensionierung mit 0.7 V zu berücksichtigen.
17.
Gegeben ist folgende Stabilisierungsschaltung mit einer Z-Diode, deren idealisierte I-U-Kennlinie eine Gerade sein soll:
Der differentielle Widerstand rz der Z-Diode am Arbeitspunkt (Anstieg der
Kennlinie) beträgt 10 Ω. Die Kennlinie Iz = f(U) der Z-Diode beginnt bei U =
Uz = 6 V mit Iz = 0.
Ferner sind gegeben: Uq = 20 V, Rv = 390 Ω, R = 220 Ω.
a)
Zeichnen Sie die Kennlinie der ZDiode (Sperrbereich) und ermitteln
Sie die Spannung über den Wider stand R!
b)
Welcher Spannungswert U stellt sich
in der Schaltung ein, wenn Uq auf 15V
abfällt?
c)
Nehmen Sie an, dass in der Schaltung
der Widerstand R unbekannt ist. Bis zu welchem minimalen Wert von R
funktioniert dann in der Schaltung die Spannungsstabilisierung?
d)
Berechnen Sie die Spannungsänderung ΔU bei Änderung von Uq um
+ 10 %, wobei R und Rv konstant bleiben!
18. Eine weiße GaN-Leuchtdiode soll an der Netzspannung betrieben werden. Ihre
Flussspannung beträgt 3.4 V, ihr Laststrom im Mittel 20 mA. Da die Durchbruchsspannung in Sperrrichtung für die Netzspannung nicht ausreicht, wird eine
zweite Diode antiparallel geschaltet (siehe Schaltung).
U Netz = Uˆ ⋅ sin ωt
U eff = 220V
f = 50 Hz
U F = 3.4V
a)
b)
c)
Berechnen Sie den Widerstand R so, dass durch
die Diode im Mittel gerade 20 mA fließen!
Welche Leistung wird in der Leuchtdiode und
welche wird in der Paralleldiode D (UF= 0.7 V)
umgesetzt?
Welche Möglichkeit gibt es noch, die Leistung durch die negative Halbwelle nicht in der LED umzusetzen?
19.
Für einen npn-Transistor gelten bei einer Umgebungstemperatur von 20 °C
folgende Werte: Kollektorsättigungsstrom ICS = 2 µA ;
Stromverstärkungsfaktoren AN = 0,98 und AI = 0,5 sowie die Kollektor Restspannungsgerade, deren Verlauf durch die I-U-Kennlinie eines
Widerstandes Ro = 50 Ω dargestellt wird.
Zeichnen Sie:
a)
das Ausgangskennlinienfeld in Basisschaltung (IE = 0...-5 mA, UCB =
0...6V );
b)
das AKLF in Emitterschaltung (IB = 0...100µA, UCE = 0...6V );
c)
eine Verlustleistungshyperbel für PV = 10 mW in beide
Kennlinienfelder;
d)
die Arbeitsgerade für einen Lastwiderstand R2 = 1 kΩ und Uq2 = 5 V in
das Ausgangskennlinienfeld der Emitterschaltung.
e)
Welchen Arbeitspunkt (UCE, IC, IB) muss man in der Emitterschaltung
wählen, wenn um diesen Arbeitspunkt symmetrisch mit maximaler
Amplitude ausgesteuert werden soll? Dimensionieren Sie den
Basiswiderstand R1 für Basiskonstantstromeinspeisung (UBE = 0,7 V).
20.
Für die gezeichnete Schaltung
sind gegeben:
IE = -3 mA,
IC = 2,95 mA,
R2 = 1,5 kΩ,
ûs = 2 mV,
Uq2 = 9 V,
Uq1 = 0,6 V.
Die Eingangsdiode gehorcht in
ihrer U-I-Beziehung dem
einfachen Exponentialgesetz.
Gesucht sind:
a)
IB,
b)
c)
d)
e)
f)
die Gleichstromverstärkungen AN ≈ −
IC
I
, B N ≈ C und der
IE
IB
Zusammenhang zwischen AN und BN,
die Spannungen UBE und UCE,
der differentielle Eingangswiderstand des Transistors rBE
und die Größen ΔUBE, ΔIB, ΔUCE, ΔIC, vi und vu (Die Δ-Größen werden
durch us verursacht).
Zeichnen Sie die Zeitverläufe der Ströme und Spannungen qualitativ auf
(t < t0 : us = 0 , t > t0 : us = ûs · sin ωt ).
21.
Für einen npn-Transistor ist folgender Arbeitspunkt gegeben:
IC = 2mA ; UCE = 6V ; IB = 6µA ; UBE = 0,6V.
a)
Zeichnen Sie je eine Emitterverstärkerstufe mit Basisstromeinspeisung
1.)
über einen Vorwiderstand R1 direkt von der Betriebsspannung her
2.)
über R1 vom Kollektor her und
3.)
über einen Spannungsteiler R1 und R3 von der Betriebsspannung
her und mit Emitterwiderstand R4, der wechselspannungsmäßig
mit einem Kondensator überbrückt ist.
b)
Berechnen Sie für jede Schaltung die Werte der benötigten Widerstände,
wenn die Betriebspannung 12V beträgt! Vorgaben: IR3 = 10 · IB und UR4
= 1,4 V.
c)
Zeichnen Sie die vollständigen Kleinsignalersatzschaltbilder für die drei
Emitterschaltungen auf! Bezeichnen Sie alle Ersatzelemente sowie alle
Spannungen und Ströme unter Angabe von Pfeilen für die positiven
Strom- und Spannungsrichtungen!
d)
Berechnen Sie für die Schaltung 1 den Eingangswiderstand ze, die
Spannungsverstärkung vu und die Stromverstärkung vi, wenn für den
angegebenen Arbeitspunkt folgende h-Parameter gelten:
h11e = 3,5 kΩ; h12e = 1,4 · 10-4; h21e = 330; h22e = 14 µS.
22.
Von einem Si-npn-Transistor ist nachstehendes Kennlinienfeld (KLF) in allen
vier Quadranten gegeben:
a.)
Wählen Sie einen geeigneten Arbeitspunkt für eine Emitterverstärkungsschaltung für IC=10 mA unter Verwendung einer Versorgungsspannung
von Uq=12V aus, markieren Sie den Arbeitspunkt in allen vier
Quadranten des Kennlinienfeldes und lesen Sie die Werte für UCE, IC, IB
und UBE ab. Berechnen Sie die Gleichstromverstärkung BN des
Transistors im Arbeitspunkt.
b.)
Zeichnen Sie die Stromübertragungskennlinie IC=f(IB) für UCE=2V in den
II. Quadranten ein.
c.)
Entwerfen Sie eine Emitterverstärkungsschaltung mit Basiskonstantstromeinspeisung von der Betriebsspannung (Uq=12V) und
dimensionieren Sie die Widerstände.
d.)
Ermitteln Sie graphisch aus dem Kennlinienfeld die vier heKleinsignalparameter. Wie kann man diese bestimmen, wenn man auf
den II. und IV. Quadranten des KLF verzichtet?
e.)
Bestimmen Sie unter Verwendung der selbstermittelten Kleinsignalparameter die Stromverstärkung Ihrer Schaltung.
Kennlinienfeld des npn-Transistors nach Aufgabe 22
23.
Gegeben ist folgende Schaltstufe:
a)
b)
c)
d)
24.
UCC = 9 V
RC = 75 Ω
BN = 120
Rrest = 15 Ω
UBEX = 0,7 V
ICBO ≤ 25 nA bei UCB= 20 V
Ptot = 200 mW
: UE = -3 V
t < to
to ≤ t ≤ t1 : UE = 5 V
: UE = -3 V
t1 ≤ t
Zeichnen Sie das Ausgangskennlinienfeld mit Lastkennlinie und
Verlustleistungshyperbel. Welche Arbeitspunkte stellen sich ein?
Welche Verlustleistungen werden im EIN- und im AUS-Zustand im Transistor
umgesetzt?
Berechnen Sie RB für m = 2. (m ist der Übersteuerungsfaktor. Er ist das
Vielfache, um den der Basisstrom erhöht wird, damit ein guter EIN-Zustand
erreicht wird. IB=m·IC/BN)
Welcher EIN-Arbeitspunkt stellt sich ein, wenn man diese Schaltung mit UCC =
12V betreibt bzw. wenn man einen Transistor mit BN = 40 einsetzt?
Über welchen Bereich kann der Arbeitspunkt schwanken, wenn für RC und RB
Widerstände mit der Toleranzklasse ± 20% verwendet werden?
Geben Sie schematisch die Bauelementequerschnitte, die Symbole, die Ausgangs- und
Übertragungskennlinienfelder aller Ihnen bekannten
MOS-FETs und SFETs an! Erklären Sie die
Kennlinienverläufe anhand der Wirkungsweise.
Für die gezeichnete Schaltung sind gegeben:
UDD = 25 V
UT = 0,8 V
K = 0.4545 mA/V2
a) Zwischen welchen Werten kann sich R2 ändern,
wenn dabei der Strom durch R2 konstant auf einem Wert von 2,5 mA bleiben
soll (Konstantstromquelle)?
Berechnen Sie R1 und R3 so, dass der Querstrom durch den Spannungsteiler
etwa 10 µA beträgt! Für welche Nennleistung muss R3 ausgelegt sein?
b) Welche Spannungsverstärkung hat diese Schaltung bei R2 = 15 kΩ und UDD =
12 V im Niederfrequenzbereich mit der unteren Grenzfrequenz fu = 20 Hz?
Die Ankopplung des NF-Signals erfolgt durch einen Koppelkondensator C =
1µF.
25. Ermitteln Sie für einen idealen Operationsverstärker (Verstärkung ∞, Eingangswiderstand ∞, Ausgangswiderstand 0, Offsetspannung 0) die Verstärkung für
folgende Schaltungen:
a)
invertierender Verstärker
b)
nichtinvertierender Verstärker
26. Ermitteln Sie für die beiden folgenden Schaltungen UA(t), wenn die
Eingangsspannung zum Zeitpunkt t = 0 von Null auf UE springt:
a)
b)
Der Operationsverstärker sei dabei bis auf eine endliche Verstärkung ideal. Durch
welche einfachen Schaltungen lassen sich die Ergebnisse wiedergeben?