6. Übung - TU Chemnitz

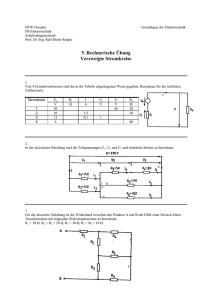
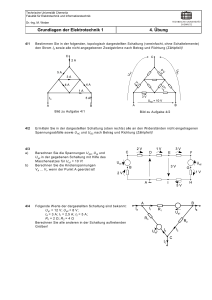
Technische Universität Chemnitz
Fakultät für Elektrotechnik und Informationstechnik
Dr.-Ing. M. Weber
Grundlagen der Elektrotechnik 3
6. Übung
6/1
Gegeben sei die Reihenschaltung aus einem ohmschen
Widerstand und einer Induktivität.
Zur Zeit t = 0 wird der Schalter von Stellung 2 auf Stellung 1
umgelegt. uq(t) sei eine Gleichspannungsquelle.
Berechnen Sie mit Hilfe der Laplace-Transformation den Verlauf
des Stromes i L(t)
a)
b)
wenn die Induktivität im Schaltmoment stromlos war und
wenn noch ein Strom I0 geflossen ist!
6/2
An die gegebene Schaltung wird zur Zeit t = 0 eine
Gleichspannung angeschlossen. Die Kapazität ist zu diesem
Zeitpunkt ungeladen.
Berechnen Sie mit Hilfe der Laplace-Transformation die
Spannung uC(t), ohne die Differentialgleichung aufzustellen!
6/3
Gegeben sei die rechts gezeigte Schaltung mit zwei
Speicherelementen. Zur Zeit t = 0 wird die Stromquelle mit dem Wert
Iq durch Öffnen des Schalters wirksam (Sprung). Der Kondensator
sei ungeladen und auch der Spulenstrom sei gleich Null gewesen.
Ermitteln Sie mit Hilfe der Laplace-Transformation die
Differentialgleichung zur Berechnung von i L (t)!
6/4
a) Berechnen Sie die Übertragungsfunktion H ( s) der dargestellten Schaltung!
b) Ermitteln Sie die Ausgangsspannung ua (t ) für den Fall, dass am Eingang ein Sprung
ue (t ) = U 0 ⋅ σ (t ) wirksam ist, mit Hilfe der Laplace-Transformation!
Hinweis: uC ( − 0) = i L ( − 0) = 0
ue ( t )
ua ( t )