1. Rationale Zahlen 1 - Maria-Theresia

Maria-Theresia-Gymnasium München
Grundwissen Mathematik
7. Klasse Algebra
1. Rationale Zahlen
Beispiele:
Negative Zahlen
Man unterscheidet positive und negative Zahlen durch
− 3; − 19564,67; − 3 sind negative Zahlen.
ihr Vorzeichen. −5 hat ein negatives Vorzeichen, +5
7
hat ein positives Vorzeichen, die Zahl 0 ist weder positiv noch negativ.
-1,5
Die Menge Q der rationalen Zahlen besteht aus den
positiven und negativen (Bruch-)Zahlen sowie der
Zahl 0. Q = ba a, b ∈ Z, b ≠ 0
{
-3
}
-2
-1
0
1
2
3
Es gilt: IN ⊂ Z⊂ Q
Absoluter Betrag
-a ist die Gegenzahl von a.
Die Entfernung eines Punktes a vom Nullpunkt der
Zahlengeraden heißt (absoluter) Betrag der Zahl a.
Der Betrag wird mit |a| bezeichnet.
Anordnung in Q
Von zwei rationalen Zahlen ist diejenige die größere,
die weiter rechts auf der Zahlengeraden liegt.
-5 ist die Gegenzahl von +5 und umgekehrt ist +5
die Gegenzahl von -5.
|-2,7| = 2,7; |0| = 0; |5,1| = 5,1.
-4,1 > -5,1 ; -3 < 4; − 1 31 < − 34
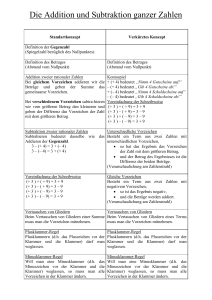
Addition und Subtraktion rationaler Zahlen
Zwei rationale Zahlen mit gleichen Vorzeichen werden
addiert, indem man die Beträge addiert und anschlie- ( −4) + ( −7) = −11; 15,8 + ( +72,6) = 88,4.
ßen das gemeinsame Vorzeichen setzt.
Zwei rationale Zahlen mit verschiedenen Vorzeichen
werden addiert, indem man vom größeren Betrag den
kleineren Betrag subtrahiert und anschließend das
Vorzeichen der Zahl mit dem größeren Betrag setzt.
Das Subtrahieren einer Zahl erfolgt durch das Addieren ihrer Gegenzahl:
a – (+b) = a + (–b);
a – (–b) = a + (+b).
Multiplikation und Division rationaler Zahlen
Man multipliziert (bzw. dividiert) rationale Zahlen, indem man ihre Beträge multipliziert (bzw. dividiert) und
das Vorzeichen nach folgender Regel setzt:
Plus
Plus
Minus
Minus
· Plus
· Minus
· Plus
· Minus
= Plus ;
= Minus;
= Minus;
= Plus ;
Plus : Plus
Plus : Minus
Minus : Plus
Minus : Minus
= Plus
= Minus
= Minus
= Plus
Verbindung der Grundrechenarten
Wie bisher gelten die Regeln:
• „Was in Klammern steht, wird zuerst berechnet“
• „Potenz vor Punkt vor Strich“
( −4) + ( +7) = +3;
2
3
+ ( − 56 ) = − 61 .
−8 − ( +19 ) = −8 + ( −19) = −27;
(+15,1) – (−23,3) = (+15,1) + (+23,3) = 38,4;
7,5 – 12,3 = −4,8
5 ⋅ (−1) = −5; (− 3 ) ⋅ 2 = − 3 .
4 5
10
( −5) ⋅ ( −9) = 45; ( − 51 ) ⋅ ( −2 31 ) = ( − 51 ) ⋅ ( − 73 ) =
12 : ( −5) = −2,4; ( − 34 ) :
( −5) : ( −9) = 59 ;
2
5
7
.
15
= − 34 ⋅ 52 = − 15
= −1 78 .
8
( −5) : ( − 31 ) = ( −5) ⋅ ( −3) = 15.
12,5 · 0 = 0;
0 : (-7,5) = 0;
Aber: durch 0 kann man nicht dividieren.
(1 −
=
11
12
1
3
: 2 2 ) ⋅ ( − 34 ) = (1 −
1
3
1
: 4) ⋅ ( − 34 ) = (1 − 12
) ⋅ ( − 34 ) =
11
⋅ ( − 34 ) = − 16
.
2. Terme und Termumformungen
Variable und Term
Ein Zeichen, das man als Platzhalter für Zahlen verwendet, heißt Variable.
Ein Ausdruck, der aus Zahlen, Variablen, Rechenzeichen und Klammern zusammengesetzt ist, heißt
Term.
Termarten:
Summe, Differenz, Produkt, Quotient, Potenz.
Beispiele für Terme:
T(x) = x + 3 , T(y) = (3 − 2y)3 , T(a;b) =
a3
−b.
5
T(x;y) = (5+x)(2-3y); T(-2;5) = 3·(-13) = –39.
Der Term ist ein Produkt.
Seite 1 von 2
Januar 2004
Maria-Theresia-Gymnasium München
Grundwissen Mathematik
Äquivalenz von Termen
Zwei Terme T1(x) und T2(x) heißen äquivalent, wenn
sie für jede Einsetzung von x jeweils den gleichen
Wert annehmen.
Es gilt dann: T1(x) = T2(x)
Rechnen mit Termen
Terme wie 5xy und 7xy, die sich nur im Koeffizienten
unterscheiden, werden addiert (bzw. subtrahiert),
indem man die zugehörigen Koeffizienten addiert
(bzw. subtrahiert) und die gemeinsamen Variablen
beibehält.
Klammerregeln
Plusklammern:
Steht ein Pluszeichen vor einer Klammer, so kann die
Klammer weggelassen werden.
Minusklammern:
Steht ein Minuszeichen vor einer Klammer, so kann
man die Klammer samt Minuszeichen weglassen,
wenn man alle Vorzeichen in der Klammer ändert.
Ausklammern (Faktorisieren)
Durch Ausklammern gemeinsamer Faktoren lassen
sich Summen in Produkte verwandeln (faktorisieren).
Multiplikation von Summen
Zwei Summen werden multipliziert, indem man jeden
Summanden der ersten Summe mit allen Summanden der zweiten Summe multipliziert und anschließend die Produkte addiert.
Die binomischen Formeln
1.
2.
7. Klasse Algebra
Die Terme 2x + 3x und 5x sind äquivalent;
die Terme 1 + x und 1 + x2 sind nicht äquivalent.
3x – 3 + 8x – x + 5 = 10x + 2
x + 2,5x2 – 4,3x – 1,9x2 = – 3,3x + 0,6x2
a + (b – c) = a + b – c
3xy + (4xy – 5x) = 3xy + 4xy – 5x = 7xy – 5x
a – (b – c) = a – b + c
7,2 – ( –5 + 6 – 2) = 7,2 + 5 – 6 + 2 = 8,2
ab + ac = a(b + c)
6xy + 3x2 – 9xz = 3x(2y + x – 3z)
3(u + v) – u(u + v) = (u + v) (3 – u)
(a + b)(c + d) = ac + ad + bc + bd
(2x + 4y)(3x – y) = 6x2 – 2xy + 12xy – 4y2.
(1,5x + y )2 = 2,25x2 + 3xy + y2
(a + b)2 = a 2 + 2ab + b 2
(a − b)2 = a 2 − 2ab + b 2
(a + b)(a − b) = a 2 − b 2
(1 − a3 )2 = 1 − 23a + a9 2
3.
(8v + 3w )(8v − 3w ) = 64v 2 − 9w 2
Mit Hilfe der binomischen Formeln kann man eben2 + 4x + 2x2 = 2 (1 + x)2.
falls Summen faktorisieren.
3. Lineare Gleichungen und Ungleichungen
Lineare Gleichungen
In einer linearen Gleichung kommt nur eine Variable
vor und diese nur in der ersten Potenz.
Um eine lineare Gleichung zu lösen, darf
• auf beiden Seiten der Gleichung dieselbe Zahl
oder derselbe Term addiert (bzw. subtrahiert)
werden,
• auf beiden Seiten der Gleichung mit derselben
von Null verschiedenen Zahl multipliziert (bzw.
dividiert) werden.
Diese Umformungen heißen Äquivalenzumformungen.
Eine lineare Gleichung mit der Grundmenge Q ist
entweder eindeutig lösbar oder nicht lösbar oder allgemeingültig.
– 2x + 48 = 12 – 11x
9x + 48 = 12
9x = – 36
x=–4
L = {– 4}
3·(2 – x) + 5x = 2x + 6
6 – 3x + 5x = 2x + 6
6 + 2x = 2x + 6
6=6
L=Q
Lineare Ungleichungen
Beim Lösen von linearen Ungleichungen ist zusätzlich
zu beachten, dass sich bei der Multiplikation (bzw.
Division) der Ungleichung mit einer (bzw. durch eine)
negative(n) Zahl das Ungleichheitszeichen umkehrt.
Seite 2 von 2
| +11x
| – 48
| :9
(Klammern auflösen)
(Zusammenfassen)
| -2x
(allgemein gültig)
– 3x < 6
| : (– 3)
x > –2
L = {x | x > –2}
Januar 2004