Theorie LU 62/63 Primzahlen, Quadratzahlen

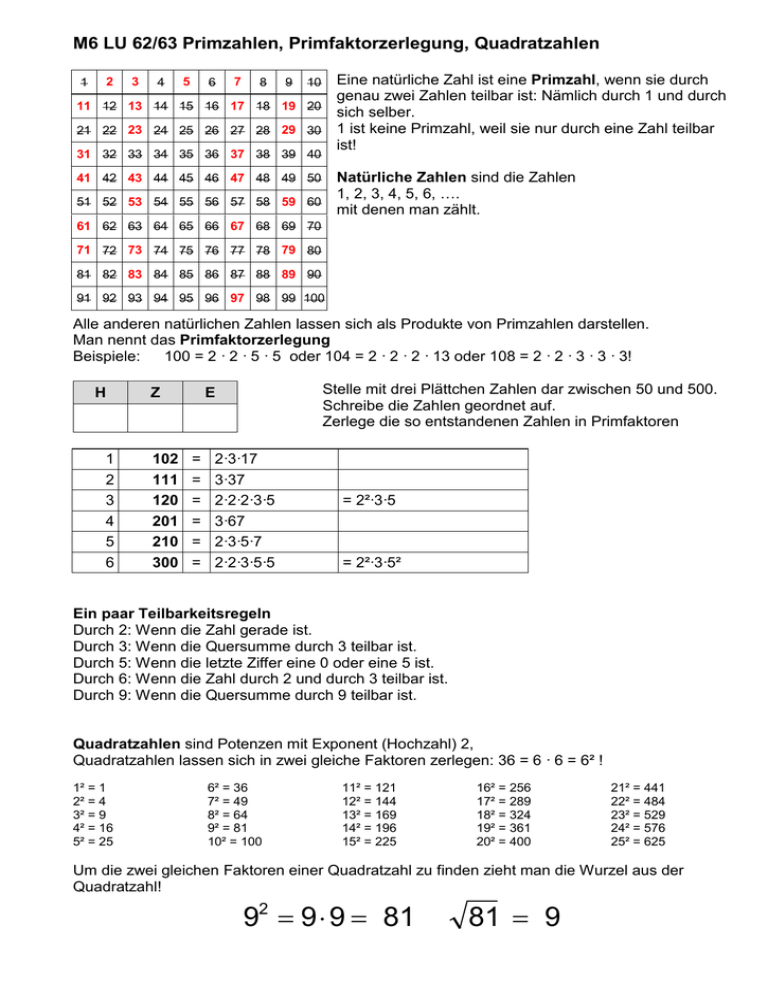
M6 LU 62/63 Primzahlen, Primfaktorzerlegung, Quadratzahlen
Eine natürliche Zahl ist eine Primzahl, wenn sie durch
genau zwei Zahlen teilbar ist: Nämlich durch 1 und durch
11 12 13 14 15 16 17 18 19 20
sich selber.
21 22 23 24 25 26 27 28 29 30 1 ist keine Primzahl, weil sie nur durch eine Zahl teilbar
ist!
2
1
3
4
5
6
7
8
9
10
31 32 33 34 35 36 37 38 39 40
Natürliche Zahlen sind die Zahlen
1, 2, 3, 4, 5, 6, ….
51 52 53 54 55 56 57 58 59 60
mit denen man zählt.
41 42 43 44 45 46 47 48 49 50
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
Alle anderen natürlichen Zahlen lassen sich als Produkte von Primzahlen darstellen.
Man nennt das Primfaktorzerlegung
Beispiele:
100 = 2 · 2 · 5 · 5 oder 104 = 2 · 2 · 2 · 13 oder 108 = 2 · 2 · 3 · 3 · 3!
H
1
2
3
4
5
6
Z
102
111
120
201
210
300
Stelle mit drei Plättchen Zahlen dar zwischen 50 und 500.
Schreibe die Zahlen geordnet auf.
Zerlege die so entstandenen Zahlen in Primfaktoren
E
=
=
=
=
=
=
2·3·17
3·37
2·2·2·3·5
3·67
2·3·5·7
2·2·3·5·5
= 2²·3·5
= 2²·3·5²
Ein paar Teilbarkeitsregeln
Durch 2: Wenn die Zahl gerade ist.
Durch 3: Wenn die Quersumme durch 3 teilbar ist.
Durch 5: Wenn die letzte Ziffer eine 0 oder eine 5 ist.
Durch 6: Wenn die Zahl durch 2 und durch 3 teilbar ist.
Durch 9: Wenn die Quersumme durch 9 teilbar ist.
Quadratzahlen sind Potenzen mit Exponent (Hochzahl) 2,
Quadratzahlen lassen sich in zwei gleiche Faktoren zerlegen: 36 = 6 · 6 = 6² !
1² = 1
2² = 4
3² = 9
4² = 16
5² = 25
6² = 36
7² = 49
8² = 64
9² = 81
10² = 100
11² = 121
12² = 144
13² = 169
14² = 196
15² = 225
16² = 256
17² = 289
18² = 324
19² = 361
20² = 400
21² = 441
22² = 484
23² = 529
24² = 576
25² = 625
Um die zwei gleichen Faktoren einer Quadratzahl zu finden zieht man die Wurzel aus der
Quadratzahl!
92 = 9 ⋅ 9 = 81
81 = 9