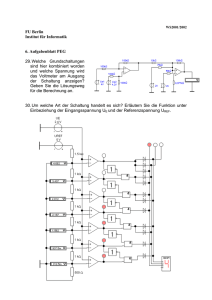
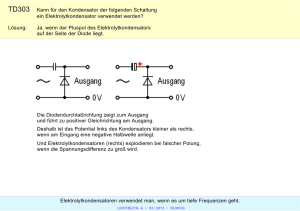
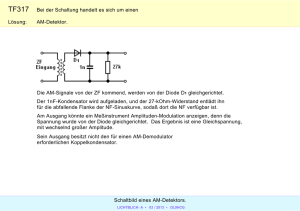
Grundlagen

Grundlagen
Ohmsches Gesetz
U=I*R
I=
U
R
R=
U
I
U in Volt
I in Ampere
R in Ohm
Elektrischer Leitwert
Der Leitwert G ist der Kehrwert des Widerstandes R
G=
1
R
G in Siemens (S)
R=
1
G
R in Ω
Effektivwert und Scheitelwert
δ ,t
Die Effektivwerte U und I von Wechselspg. Und -strom entwickeln in einem Ohmschen Widerstand
die gleiche Leistung P wie ein ebenso großer Gleichstrom und eine ebenso große Gleichspg.
Bei sinusförmigem Verlauf gilt:
U = 0,707 * Umax
I = 0,07 * Imax
Damit ergibt sich für die Scheitelwerte:
Umax =
Imax =
U
= 1,414 * U
0,707
I
= 1,414 * I
0,707
1,414 =
0,707 =
2
1
2
Energieumwandlung und Wirkungsgrad
Energie kann weder erzeugt noch verlorengehen. Sie wird immer von einer Art in eine andere
umgewandelt.
Der Energieverlust Wv bei Energieumwandlungen ist der Unterschied zwischen zugeführter
Energie WZu und ausgenutzter Energie WAb.
WV = WZu - WAb
Für den Leistungsverlust PV gilt dementsprechend
PV = PZu - PAb
Der Wirkungsgrad η ist das Verhältnis von genutzter Energie WAb zu zugeführter Energie WZu
η =
W Ab
WZu
und entspricht
η
PAb
PZu
Neben der Einheit Kilowatt (kW) hat man zur Angabe der Leistung von Wärmekraftmaschinen die
Pferdestärke (PS) verwendet Für sie gelten die Beziehungen:
1 PS = 0,736 kW
1 kW = 1,36 PS
Zusammenschalten mehrerer Spannungserzeuger
Reihenschaltung
Die EMK der einzelnen Spgserzeuger werden zur Gesammt-EMK addiert.
E = E1 + E2 + E3 + En
Die Innenwiderstände der einzelnen Spgserzeuger werden zum Gesammtinnenwiderstand addiert.
Ri = Ri1 + Ri2 + Ri3 + Rin
Parallelschaltung
Parallel zu schaltende Spgserzeuger müssen gleiche EMK haben. Die Gesamt EMK ist so groß wie
die EMK jedes einzelnen Spgserzeugers.
E = E1 = E2 = E3 = En
Wie bei der Parallelschaltung von Verbraucherwiderständen gilt für den Ersatzinnenwiderstand die
Formel.
1
Ri
1
Ri 1
1
Ri 2
1
R i3
1
R in
Leitwiderstand
Der Widerstand eines Leiters hängt vom Querschnitt, der Länge und vom Material ab.
m
Ω *mm 2
l
R=
*A
Einheit von γ (gamma) =
Silber
67
Kupfer
56
Gold
45
Aluminium
35
Merksatz: Spez. Widerstand ist der Widerstand eines Leiters von 1 m Länge und 1mm 2 Querschnitt
bei + 20C°
Einheit von δ (roh) =
Ω * mm 2
m
R=
*l
A
Tabellen Periodensystem
Die elektrische Leitfähigkeit der chemischen Elemente
(die besten 25, bei 20°C)
Stellung
Name
Symbol
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
25
Silber
Kupfer
Gold
Aluminium
Calcium
Beryllium
Natrium
Magnesium
Rhodium
Molybdän
Iridium
Wolfram
Zink
Cobalt
Nickel
Cadmium
Kalium
Ruthenium
Osmium
Indium
Lithium
Eisen
Platin
Zinn
Ag
Cu
Au
Al
Ca
Be
Na
Mg
Rh
Mo
Ir
W
Zn
Co
Ni
Cd
K
Ru
Os
In
Li
Fe
Pt
Sn
Elektrische Spezif. elektr. Bezogen
Leitfähigkeit Widerstand auf Silber
(S/m)
(%)
62,89
59,77
42,55
37,66
29,15
23,81
21,50
22,62
22,17
19,20
18,83
17,69
16,90
16,02
14,60
13,30
13,14
13,12
12,31
11,94
11,69
10,29
9,48
9,09
0,01590
0,01673
0,02350
0,026548
0,0343
0,0420
0,0465
0,0442
0,0451
0,0520
0,0531
0,0565
0,05916
0,0624
0,0685
0,0750
0,0761
0,0762
0,0812
0,0837
0,0855
0,0971
0,1054
0,1100
100
95,04
67,66
59,88
46,35
37,86
34,18
35,97
35,25
30,53
29,94
28,12
26,87
25,47
23,22
21,14
20,90
20,86
19,57
18,98
18,59
16,36
16,78
14,46
Vom FARBCODE zum Widerstandswert
silber
gold
schwarz
braun
rot
orange
gelb
grün
blau
violett
grau
weiß
1. Ziffer
(IEC)
1
2
3
4
5
6
7
8
9
keine
-
Kennfarbe
2. Ziffer (IEC) Dekade
Toleranz
0
1
2
3
4
5
6
7
8
9
10-2
10-1
100 = 1
101
102
103
104
105
106
-
±10%
±5%
±1%
±2%
±0,5%
±0,25%
±0,1%
-
-
-
±20%
Beispiel für 4-Farben-Code
Bevor man den Farbcode in den Widerstandswert verwandeln kann, muß man sich erst
vergewissern, daß man die Farbringe in der richtigen Reihenfolge liest.
Der erste Farbring ist jener, der ganz knapp beim Gehäuserand aufgetragen wurde. Ist der
Widerstandskörper groß genug, ist der vierte Ring, der, der den Toleranzwert angibt,
etwas abgesetzt.
Der Widerstandswert entsteht aus einer zweistelligen Zahl (IEC-Zahl), multipliziert mit der
Dekade; unser Beispiel:
1. Ring: grün = 5
2. Ring: blau = 6
3. Ring: rot = 10² = 100 ergibt: 56 . 100 = 5 600 Ω (sprich: Ohm)
4. Ring: gold = ±5% Toleranz
5% von 5 600 sind 280, d.h. der Nennwert von 5 600 Ω kann in Wirklichkeit maximal um
280 Ω kleiner (5 320 Ω) oder maximal um 280 Ω größer (5 820 Ω) sein.
Das Ergebnis lautet also 5 600 Ω . Wir merken uns:
Zahlen > 1 000 Ω werden in 1 kΩ (sprich: 1 Kilo Ω) umgewandelt,
Zahlen > 1 000 000 Ω werden in 1 MΩ (sprich: 1 Mega Ω) umgewandelt.
Womit das endgültige Ergebnis 5,6 kΩ beträgt.
.
Beispiel für 5-Farben-Code
Hat ein Widerstand fünf Farbringe, so bildet eine dreistellige Zahl, multipliziert mit der
entsprechenden Zehnerpotenz, den Widerstandswert.
1. Ring: grün = 5
2. Ring: blau = 6
3. Ring: schwarz = 0
4. Ring: braun = 101 = 10 ergibt: 560 . 10 = 5 600 Ω
5. Ring: rot = ± 2% Toleranz
Endergebnis: 5,6 kΩ / ± 2% Toleranz
. IEC-Reihen
Eine IEC (International Electrotechnical Commission)-Reihe gibt die Abstufung der
Nennwerte innerhalb einer Dekade an.
Bei der E6, der ältesten Reihe, gibt es zwischen 0 und 10 sechs Nennwerte und eine
Toleranz von 20%. Bei der E12 sind es sinngemäß 12 Nennwerte und 10%, bei der E24
.....
Man hat zwar mit Hilfe des Ohm'schen Gesetzes einen Widerstandswert von z.B. 64 Ω
errechnet, kaufen wird man diesen Widerstand aber nicht können. Laut E24 gibt es im
Handel nur 62 Ω oder 68 Ω.
Die Zahlen in den Reihen wurden so gewählt, daß es aufgrund der Toleranz zu
geringfügigen Überschneidungen kommt. Braucht man einen exakten Wert, muß man auf
Trimmpotentiometer oder Spindeltrimmer zurückgreifen.
E6 ±20%
E12 ±10%
E24 ±5%
1,0
.
.
.
1,5
.
.
.
2,2
.
.
.
3,3
.
.
.
4,7
.
.
.
6,8
.
.
.
20%
1,0
.
1,2
.
1,5
.
1,8
.
2,2
.
2,7
.
3,3
.
3,9
.
4,7
.
5,6
.
6,8
.
8,2
.
10%
1,0
1,1
1,2
1,3
1,5
1,6
1,8
2,0
2,2
2,4
2,7
3,0
3,3
3,6
3,9
4,3
4,7
5,1
5,6
6,2
6,8
7,5
8,2
9,1
5%
.
Temperaturabhängigkeit des Widerstandes
Rw = R K * (1 + α * ∆t )
∆t =
Rw − R K
Rk *α
Rw = Warmwiderstand
α = Temperaturbeiwert
∆t = Temperaturänderung
Temperaturbeiwerte
Eisen
Silber
Gold
Kupfer
Alu
Kohle
0,005
0,0041
0,0039
0,0039
0,0036
-0,00045
Merksatz:Der Widerstand von Kaltleitern (Metalle) nimmt bei
Temperaturerhöhung zu.
Merksatz:Der Widerstand von Heißleitern (Kohle) nimmt bei
Temperaturerhöhung ab.
Permabilitätszahlen
Feromag. Stoffe
Eisen unlegiert bis 6000
Dynamoblech > 6500
Eisen – Nickel Legierungen bis 300.000
Weichmagn. Ferrite > 10.000
Paramagnetische Stoffe
Luft 1,0
Sauerstoff, Alu, Platin ~ 1,00002
Diamagn. Stoffe
Quecksilber, Silber, Zink ~ 0,99
Wasser ~ 0,89
Elektrotechnik
1. Kirchhoffsches Gesetz (Knotenregel):
An einem Knoten sind die Summen aller Ströme 0
Dabei sind zufließende Ströme positiv und
abfließende Ströme negativ einzusetzen.
In einer Parallelschaltung von Widerständen verhalten
sich der Gesamtstrom und die einzelnen Teilströme
umgekehrt wie der Gesamtwiderstand R und die zu
den Teilströmen gehörenden Widerstände.
2. Kirchhoffsches Gesetz(Maschenregel)
In einer geschlossenen Stromkreismasche ist die Summe aller Spg. 0.
Dabei sind in Zählpfeilrichtung durchlaufende Spg. positiv, gegen die Zählpfeilrichtung laufende
negativ einzusetzen.
In einer Reihenschaltung von Widerständen verhalten sich die Teilspannungen wie die zugehörigen
Widerstände.
Spule im Wechselstromkreis
Induktiver Widerstand: Eine vom Wechselstrom durchflossene Spule hat
Außer ihrem Wirkwiderstand R einen induktiven Widerstand XL, der mit der Induktivität L der
Spule und mit der Frequenz f des Wechselstroms zunimmt.
U
R
XL
Der Scheinwiderstand Z ist der wirksame Wechselstromwiderstand der Spule.
Er kann geometrisch als Hypotenuse eines rechtwinkeligen Dreiecks, dessen Kathethen der
Wirkwiderstand R und der induktive Widerstand XL sind , dargestellt werden. (Widerstandsdreieck).
Im Widerstandsdreieck gelten folgende Beziehungen:
Z2= R 2 + X L
Z=
U
I
Z=
XL =
U
I
UL
I
R
Z
X
sin ϑ = L
Z
cos ϑ =
Z,R und XL in Ω
2
Widerstandsdreieck
Nach dem Ohmschen Gesetz enthält man:
U=I*Z
UR = I *R
UL = I * XL
Für das Spannungsdreieck gilt:
U
UR
U2 = U2R + U2L
U
cos ϑ = R
U
U
sin ϑ = L
U
UL
Bsp.:
Eine Spule nimmt an der Gleichspannung U = 12 V den Strom I = 0.5 A auf. Bei der Wechselspg.
U = 220V~ mit der Frequenz f = 50 HZ fließt der Wechselstrom I~ = 4 A. Wie groß sind die
Wiederstände R,Z und XL, die Induktivität L, Der Phasenverschiebungswinkel ϕ zwischen Spg. und
Strom sowie die Wirkspg. UR und die Induktive Blindspg. UL?
Lösung:
Wirkwiders tan d R =
U − 12
= 24Ω
I − 0.5
Scheinwiders tan d Z =
U ~ 220
=
= 55Ω
I~
4
Durch den Verlustwiderstand ist der Wirkwiderstand bei Wechselstrom allerdings größer als der
Gleichstromwiderstand 24Ω.
Den Induktiven widerstand XL erhält man mit der Formel Z2 = R2 + XL2 . Subtrahiert man auf beiden
Seiten R2 und zieht anschließend auf beiden Seiten der Gleichung die Wurzel, so ergibt sich
X L = Z 2 − R 2 = 55 2 − 24 2 = 49,5Ω
Aus dem Widerstandsdreieck erhält man
cos ϑ =
R 24
= =,436 und daraus aus der Sinustafel ϑ = 64°
Z 55
Ferner findet man
UR = I * R = 4 * 24 = 96V und
UL = I * XL = 4 * 49,5 = 198V
Leistung und Arbeit
Bsp.:
Ein Wechselstrommotor für U = 220V nimmt den Betriebsstrom I = 5A auf. Mit einem
Leistungsmesser wird die Wirkleistung P = 800W gemessen. Wie groß ist die Scheinleistung S, der
Leistungsfaktor cosϕ, die Blindleistung QL sowie der Wirkstrom IR und der Blindstrom IL des
Motors? Welchen Energieverbrauch zeigt ein Zähler nach 8 Betriebsstunden an?
Lösung:
Scheinleistung S = U * I = 220 * 5 = 1,1 kVA
P
800
Leistungsfaktor cosϕ =
=
= 0,73
U * I 1100
Aus einer Sinustafel entnimmt man ϕ = 43° und sinϕ = 0,682
Wirkstrom IR = I * cosϕ = 5 * 0,73 = 3,65A
Blindstrom IL = I * sinϕ = 5 * 0,682 = 3,41A
Blindleistung QL = U * I * sinϕ = 220 * 5 * 0,682 = 0,750kVar
Der Zähler mißt in 8h die Wirkarbeit
W = P * t = 800 *8 = 6,4kWh
Drehstrom
S=
3 *U*I
P=
3 * U * I * cos α
Q=
3 * U * I * sin α
Q=
S2 − P2
Wie groß ist die Leistungsaufnahme eines Elektrowärmegerätes mit 3 Heizwiderständen von je
100 Ω , wenn diese in a) Stern und b) in Dreieck geschalten an 380 V gelegt werden?
____________________
Sternschaltung
Sternschaltung: An jedem Widerstand liegt die Strangspg. U st , daher werden Strangstrom und
Leiterstrom
IStrang =
U Strang
R
=
220V
= 2,2A und IStern = IStrang Stern = 2,2 A
100Ω
Dann ist die Leistung
P Stern = 1,73 * U * IStern = 1,73 * 380 V * 2,2 A = 1452W
Dreieckschaltung
Dreieckschaltung: An jedem Widerstand liegt die Leiterspg. daher werden Strangstrom und
Leiterstrom.
IStrang
=
U 380V
=
= 3,8 A und IDreieck = 1,73 * IStrang * 3,8 A = 6,57A
R 100Ω
Die Leistung wird P = 1,73 * U * I = 1,73 * 380V * 6,57A = 4332W
Die gesuchten Verhältniszahlen sind:
IStrang Stern : IStrang = 1 : 1,73
PStern : P = 1 : 3
Merksatz:Schaltet man an einem Netz einen Verbraucher von Sternschaltung in Dreieckschaltung
um, so steigt die Leistung auf den dreifachen Wert an
Leistung, wenn ein Überstromschutzorgan im Außenleiter auslöst.
Dreieckschaltung:
Bei Ausfall eines Überstromschutzorganes geht die Drehstromleistung auf die Hälfte zurück.
Sternschaltung:
Bei Ausfall eines Überstromschutzorganes geht die Drehstromleistung auf die Hälfte zurück.
Sternschaltung mit Sternpunktleiter:
Bei Ausfall eines Überstromschutzorganes geht die Drehstromleistung auf 2 Drittel zurück.
Kondensatorschaltungen
Reihenschaltung:
Die Reihenschaltung mehrerer Kondensatoren entspricht einer Vergrößerung des Plattenabstandes,
was also eine Kapazitätsverminderung bedeutet.
Bei der Reihenschaltung ist die Gesamtkapazität kleiner als die kleinste Einzelkapazität.
Parallelschaltung
Eine Parallelschaltung von mehreren Kondensatoren entspricht einer Vergrößerung der
Plattenoberfläche, was gleichzeitig eine Vergrößerung der Kapazität bewirkt.
Bei der Parallelschaltung ist die Gesamtkapazität gleich der Summe der Einzelkapazitäten.
Beim Anschluß an Wechselspg. fließt in einem Stromkreis mit Kondensatoren ein Wechselstrom,
der scheinbar auch durch den Kondensator fließt, sich aber in Wirklichkeit aus Lade- und
Entladeströmen zusammensetzt.
Merksatz: Beim Kondensator eilt der Strom der Spg. um 90° vor
Ladungsmenge
Formelzeichen: Q
Die in einem Kondensator gespeicherte Ladungsmenge Q wird bestimmt durch die Kapazität C
(Fassungsvermögen) des Kondensators und die an den Kondensatorplatten anliegende Spg. U
(Druck).
Ladungsmenge Q = Kapazität C * Spannung U
Q = C *U
Q in As
C in
As
(= Farad)
V
U in V
Berechnung des Kapazitiven Blindwiderstandes eines Kondensators
Xc =
1
2 *π * f * C
X c in
f in Hz
C in F
Ω
Die Ladekurve
τ
C in %
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,2
1,4
1,6
1,8
0
9,5
18
25,8
32,8
39,2
45,0
50
55
59
63
69,7
75
79,6
83,3
Ladungssteigerung in %
0
15
13,5
12,4
11,0
10
9,2
8,0
8,0
6,3
6,3
28,7
22,7
19,7
15,8
Stromwärme
Wärmemenge. Die durch den elektr. Strom erzeugte Wärmemenge Q ist der elektr. Arbeit W
verhältnisgleich.
Q = 3600 * W
Q in kJ
1 Ws = 1J
W in kWh
1 kWh = 3600 kJ
Wärmewirkungsgrad. Bei der Umwandlung elektr. Energie in Wärme entstehen Wärmeverluste
dadurch, daß ein Teil der Stromwärme auf den Gerätekörper und auf die Luft übergeht. Der
Wärmewirkungsgrad η ist das Verhältnis der Wärmemenge Q2, die der erwärmte Stoff
aufgenommen hat, zu der erzeugten Stromwärme Q1
η ohne Einheit(Eta)
η=
Q2
Q1
Q1 und Q2 in J oder kJ
Bsp.: Ein Kochtopf enthält 5 l Wasser von T1 = 20°C. Um es auf einer 800 Watt Kochplatte zum
kochen (T2 = 100°C) zu bringen, braucht man die Zeit t = 50 min. Wie groß ist der Wirkungsgrad
η?
__________________
Lösung: 5l Wasser entsprechen 5 kg Wasser. Die Temperaturerhöhung des Wassers beträgt
∆T = T2 − T1 = 100°C - 20°C = 80K. Die dazu benötigte Wärmemenge ist?
=============
Q2 = c * m * ∆T = 4,2
kJ
* 5kg * 80K = 1680 kJ
kg * K
Q
∆T
c
m
Wärmemenge
Temperaturunterschied
spez. Wärmekapazität
Masse
spez. Wärmekapazitäten
Aluminium
Kupfer
Stahl
Wasser
Die in der Zeit t = 50 min =
W = P * t = 0,8 kW *
0,92 kJ
0,39 kJ
0,46 kJ
4,19 kJ
50
h verrichtete Arbeit beträgt.
60
50
h = 0,667 kWh
60
Die erzeugte Stromwärme ist:
Q1 = 3600
kJ
* 0,667 kWh = 2400 kJ
kWh
Daraus ergibt sich der Wärmewirkungsgrad für das Kochen auf der Kochplatte:
η=
Q2 1680kJ
=
= 0,696 = 0,7
Q1 2400kJ
Transformatoren
Transformatoren sind elektrische Maschinen, die zum Umspannen von Wechsel-, oder Drehstrom
dienen.
Die Leerlaufspannungen beim Transformator verhalten sich wie die Windungszahlen.
U1
N
= 1
U2
N2
Das Verhältnis der Primär zur Sekundärwindungszahl wird als Übersetzungsverhältnis ü
bezeichnet.
N1
=ü
N2
Unter Vernachlässigung der geringen Verluste gilt bei einem belasteten Transformator:
U 1 J 2 N1
= =
=ü
U 2 J1 N 2
Die Ströme bei einem Transformator verhalten sich umgekehrt wie die Windungszahlen.
Zwischen dem Wechselstrom - Eingangswiderstand Z1 =
Z2 =
U1
und dem Ausgangswiderstand
J1
U2
sowie den Windungszahlen ergibt sich folgender Zusammenhang:
J2
U1
2
Z1
J1
U1 * J 2
N1 * N1
N1
=
=
=
=
= ü2
2
Z 2 U 2 U 2 * J1 N 2 * N 2
N2
J2
ü=
Z1
Z2
Bit and Bytes
Bit engl. Binary Digit.
Die kleinste Informationseinheit (Speicherstelle) stellt die Information durch 2 Zustände dar. In der
binären Schreibweise wird ein Bit mit 0 oder 1 dargestellt. Dies entspricht in der Speicherzelle
aus/ein oder kein Strom/Strom.
Zu beachten: 1 Kilobit = 1024 Bit
Byte:
Eine Einheit von 8 Bit. Bei der Binären Zahlendarstellung werden die Bits von 0 bis 7 numeriert,
rechts beginnend.DieWertigkeit der Bits ist hierbei 2^Bit-Nr. Für den Wert eines Bytes werden die
einzelnen Wertigkeiten der Bits, deren Information 1 ist addiert. Der größte dargestellte Wert
beträgt für 1 Byte 255 oder hexadezimal FF, dies ist der größte zweistellige Wert in hexadezimaler
Schreibweise.
Hexadezimal – sedezimal:
Um Binärzahlen Platzsparend darstellen zu können, bedient man sich des Hexadezimalsystems, das
auf der Grundlage von 16 basiert. Jeweils 4 Bit (Nibble) können in einem Zeichen dargestellt
werden. Der höchste Wert eines Zeichens ist 15, wobei die Werte 0 bis 9 als Ziffern und 10 bis 15
mit den Buchstaben A bis F dargestellt werden.
Grenzwerte sind F = 15 (Nibble), FF = 255 (Byte), FFF = 65535 (Word).
Bsp.: Binäranzeige: 1100011001010100
Dezimal:
50772
Hexadezimal: C654
Wertung Binäranzeige
0
1
0
2
1
4
0
8
1
16
0
32
1
64
0
128
0
256
1
512
1
1024
0
2048
0
4096
0
8192
1
16384
1
32768
Summe
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
Wertung Hexaanzeige
0
0
4
0
16
0
64
0
0
512
1024
0
0
0
16384
32768
50772
4
1
5
16
6
256
12
4096
Summe
=
=
=
=
4
80
1536
49152
50772
Bsp.: Binäranzeige: 0000111001100101
Dezimal:
3685
Hexadezimal: 0E65
Wertung Binäranzeige
1
1
0
2
1
4
0
8
0
16
1
32
1
64
0
128
0
256
1
512
1
1024
1
2048
0
4096
0
8192
0
16384
0
32768
Summe
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
Wertung Hexaanzeige
1
0
4
0
0
32
64
0
0
512
1024
2048
0
0
0
0
3658
5
1
6
16
14
256
0
4096
Summe
=
=
=
=
5
96
3584
0
3685
UND / AND / Konjunktion
Das UND ist eine Grundverknüpfung, die nach dem Prinzip arbeitet, wenn zwei Zustände oder
Aussagen zutreffen, dann ist das Ergebnis wahr: Wenn A und B, dann...
Der Ausgang Q ist immer dann 1, wenn die Eingänge A und B gleich 1 sind.
Das UND wird als Konjunktion bezeichnet und im englischen als AND benannt.
Schaltzeichen
Funktionsgleichung
Wahrheitstabelle
A B Q
0 0 0
0 1 0
1 0 0
1 1 1
Ersatzschaltung mit Relais
Diese logische Verknüpfung bezeichnet man als UND-Verknüpfung. Jede
Schaltung, die der Wahrheitstabelle entspricht ist eine UND-Verknüpfung.
Es gelten folgende Regeln:
•
Der Ausgang Q ist nur dann 1, wenn alle Eingänge 1 sind.
•
Der Ausgang Q ist dann 0, wenn mindestens ein Eingang 0 ist.
IC-Nr. in den Schaltkreisfamilien
TTL CMOS
7408 4081
ODER / OR / Disjunktion
Das ODER ist eine Grundverknüpfung, die nach dem Prinzip arbeitet, wenn der eine oder der
andere Zustand oder die eine oder andere Aussage zutrifft, dann ist das Ergebnis wahr: Wenn A
oder B, dann...
Der Ausgang Q ist immer dann 1, wenn die Eingänge A oder B gleich 1 sind.
Das ODER wird als Disjunktion bezeichnet und im englischen als OR benannt.
Schaltzeichen
Funktionsgleichung
Wahrheitstabelle
A B Q
0 0 0
0 1 1
1 0 1
1 1 1
Ersatzschaltung mit Relais
Diese logische Verknüpfung bezeichnet man als ODER-Verknüpfung. Jede
Schaltung, die der Wahrheitstabelle entspricht ist eine ODER-Verknüpfung.
Es gelten folgende Regeln:
•
Der Ausgang Q ist dann 1, wenn mindestens ein Eingang 1 ist.
•
Der Ausgang Q ist nur dann 0, wenn alle Eingänge 0 sind.
IC-Nr. in den Schaltkreisfamilien
TTL CMOS
7432 4071
NAND / NICHT-UND / NUND
Das NAND ist ein aus UND und NICHT zusammengeschaltetes Element. Es arbeitet wie ein UND,
dessen Ausgang negiert ist.
Der Ausgang Q ist gleich 1, wenn Ausgang A oder B gleich 0 sind.
B A X Q
0 0 0
1
0 1 0
1
1 0 0
1
1 1 1
0
Schaltzeichen
Funktionsgleichung
Wahrheitstabelle
A B Q
0 0 1
0 1 1
1 0 1
1 1 0
Ersatzschaltung mit Relais
Diese logische Verknüpfung bezeichnet man als NAND-Verknüpfung. Jede
Schaltung, die der Wahrheitstabelle entspricht ist eine NAND-Verknüpfung.
Es gelten folgende Regeln:
•
Der Ausgang Q ist 0, wenn alle Eingänge gleich 1 sind.
•
Der Ausgang Q ist 1, wenn mindestens ein Eingang gleich 0 ist.
IC-Nr. in den Schaltkreisfamilien
TTL CMOS
7400 4011
Vom NAND zum NICHT
Das NAND eignet sich auch als NICHT. Dazu werden die beiden Eingänge miteinander verbunden,
so dass dieses Verknüpfungsglied nur noch einen Eingang hat.
C B A Q
0 0 0
1
1 1 1
0
Man schaltet das NAND so, wenn man in einer digitalen Schaltung auf NICHT-Glieder verzichten
will oder keines mehr übrig hat, oder um lange Leiterbahnen zu vermeiden.
NOR / NICHT-ODER / NODER
Das NOR ist ein aus ODER und NICHT zusammengeschaltetes Element. Es arbeitet wie ein
ODER, dessen Ausgang negiert ist.
Der Ausgang Q ist immer dann 1, wenn die Eingänge A oder B gleich 0 sind.
B A X Q
0 0 0
1
0 1 1
0
1 0 1
0
1 1 1
0
Schaltzeichen
Funktionsgleichung
Wahrheitstabelle
A B Q
0 0 1
0 1 0
1 0 0
1 1 0
Ersatzschaltung mit Relais
Diese logische Verknüpfung bezeichnet man als NOR-Verknüpfung. Jede
Schaltung, die der Wahrheitstabelle entspricht ist eine NOR-Verknüpfung.
Es gelten folgende Regeln:
•
Der Ausgang Q ist 1, wenn alle Eingänge gleich 0 sind.
•
Der Ausgang Q ist 0, wenn mindestens ein Eingang gleich 1 ist.
IC-Nr. in den Schaltkreisfamilien
TTL CMOS
7402 4001
Vom NOR zum NICHT
Das NOR eignet sich auch als NICHT. Dazu werden die beiden Eingänge miteinander verbunden,
so dass dieses Verknüpfungsglied nur noch einen Eingang hat.
C B A Q
0 0 0
1
1 1 1
0
Man schaltet das NOR so, wenn man in einer digitalen Schaltung auf NICHT-Glieder verzichten
will, oder keines mehr übrig hat, oder um lange Leiterbahnen zu vermeiden.
XNOR / Exklusiv-NICHT-ODER / Äquivalenz
Das XNOR ist eine Verknüpfungsschaltung aus zwei UND, zwei NICHT und einem ODER. Die
Schaltung besteht aus drei Teilen. Zum einen werden die Eingänge UND-verknüpft (Z). Dann
werden sie zusätzlich noch negiert und anschließend UND-verknüpft (X). Beide Ergebnisse werden
dann ODER-verknüpft. Das Endergebnis (Q) entspricht dem logischen XNOR.
Die Ausgang Q ist immer dann 1, wenn die Eingänge A und B gleich sind. Also wenn beide gleich
1 oder gleich 0 sind.
B A Z
Q
0 0 0 1 1
0 1 0 0 0
1 0 0 0 0
1 1 1 0 1
Schaltzeichen
Funktionsgleichung
Wahrheitstabelle
A B Q
0 0 1
0 1 0
1 0 0
1 1 1
Ersatzschaltung mit Relais
Diese logische Verknüpfung bezeichnet man als XNOR-Verknüpfung. Jede Schaltung, die der
Wahrheitstabelle entspricht ist eine XNOR-Verknüpfung.
Es gelten folgende Regeln:
•
Der Ausgang Q ist 0, wenn alle Einänge unterschiedlich sind.
•
Der Ausgang Q ist 1, wenn alle Eingänge gleich sind.
IC-Nr. in den Schaltkreisfamilien
TTL
CMOS
74266 4077
XOR / Exklusiv-ODER / Antivalenz
Das XOR ist ein zusammengeschaltetes Element aus XNOR und NICHT. Es arbeitet wie ein
XNOR dessen Ausgang negiert wird.
Der Ausgang Q ist immer dann 1, wenn die Eingänge A und B ungleich sind.
B A X Q
Schaltzeichen
Funktionsgleichung
Wahrheitstabelle
A B Q
0 0 0
0 1 1
1 0 1
1 1 0
0 0 1
0
0 1 0
1
1 0 0
1
1 1 1
0
Ersatzschaltung mit Relais
Diese logische Verknüpfung bezeichnet man als XOR-Verknüpfung. Jede Schaltung, die der
Wahrheitstabelle entspricht ist eine XOR-Verknüpfung.
Es gelten folgende Regeln:
•
Der Ausgang Q ist 1, wenn alle Eingänge unterschiedlich sind.
•
Der Ausgang Q ist 0, wenn alle Eingänge gleich sind.
IC-Nr. in den Schaltkreisfamilien
TTL CMOS
7486 4030
Grundstromkreis
Ri = R ges − Raußen
U
k
= I * Raußen
= 16,5 V
I = 2,5 A
I Kurzschluß = 25 A
U
kl
EMK, R
EMK =
Ri
i
Ukl * IK
Ik − i
= 18,33 V
= EMK = 0,73 Ω
IK
EMK = Treibende Kraft
U = EMK – innerer Spgsabfall