Hydraulische Grundlagen

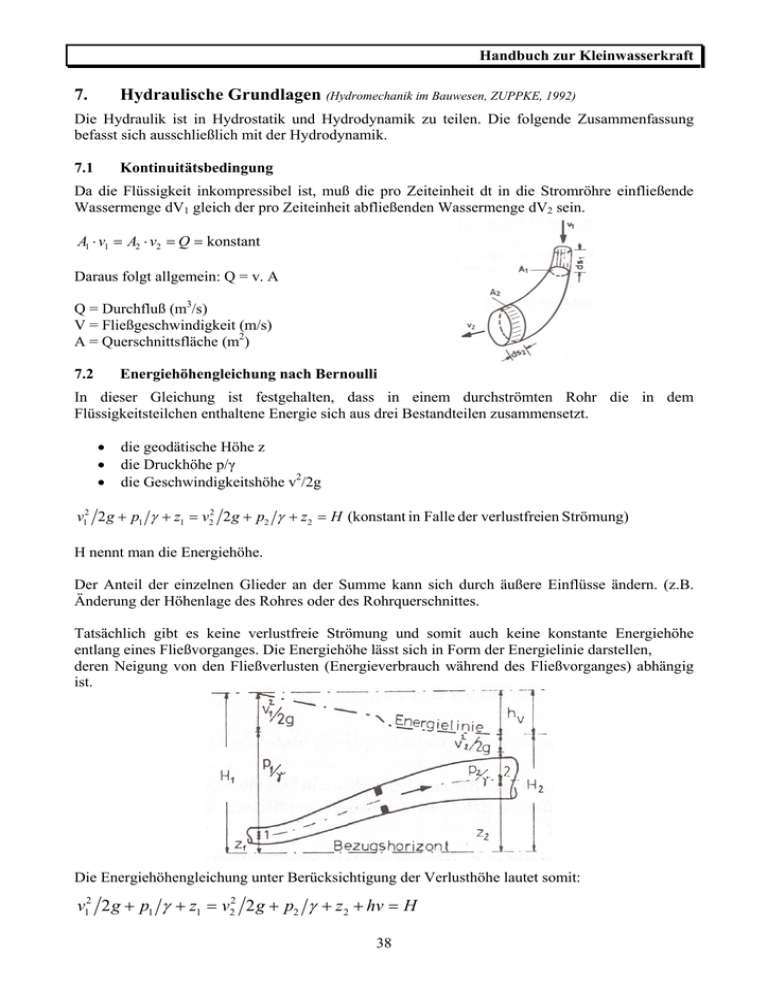
Handbuch zur Kleinwasserkraft
7.
Hydraulische Grundlagen (Hydromechanik im Bauwesen, ZUPPKE, 1992)
Die Hydraulik ist in Hydrostatik und Hydrodynamik zu teilen. Die folgende Zusammenfassung
befasst sich ausschließlich mit der Hydrodynamik.
7.1
Kontinuitätsbedingung
Da die Flüssigkeit inkompressibel ist, muß die pro Zeiteinheit dt in die Stromröhre einfließende
Wassermenge dV1 gleich der pro Zeiteinheit abfließenden Wassermenge dV2 sein.
A1 ⋅ v1 = A2 ⋅ v2 = Q = konstant
Daraus folgt allgemein: Q = v. A
Q = Durchfluß (m3/s)
V = Fließgeschwindigkeit (m/s)
A = Querschnittsfläche (m2)
7.2
Energiehöhengleichung nach Bernoulli
In dieser Gleichung ist festgehalten, dass in einem durchströmten Rohr die in dem
Flüssigkeitsteilchen enthaltene Energie sich aus drei Bestandteilen zusammensetzt.
•
•
•
die geodätische Höhe z
die Druckhöhe p/γ
die Geschwindigkeitshöhe v2/2g
v12 2 g + p1 γ + z1 = v22 2 g + p2 γ + z2 = H (konstant in Falle der verlustfreien Strömung)
H nennt man die Energiehöhe.
Der Anteil der einzelnen Glieder an der Summe kann sich durch äußere Einflüsse ändern. (z.B.
Änderung der Höhenlage des Rohres oder des Rohrquerschnittes.
Tatsächlich gibt es keine verlustfreie Strömung und somit auch keine konstante Energiehöhe
entlang eines Fließvorganges. Die Energiehöhe lässt sich in Form der Energielinie darstellen,
deren Neigung von den Fließverlusten (Energieverbrauch während des Fließvorganges) abhängig
ist.
Die Energiehöhengleichung unter Berücksichtigung der Verlusthöhe lautet somit:
v12 2 g + p1 γ + z1 = v22 2 g + p2 γ + z2 + hv = H
38
Handbuch zur Kleinwasserkraft
7.3
Abflußzustände im offenen Gerinne
Die Strömung in einem offenen Gerinne ist dadurch gekennzeichnet, dass sie mit freier
Wasseroberfläche erfolgt. Verglichen mit der Rohrströmung ist somit der Querschnitt nicht durch
äußere Einflüsse (Rohrdimension) begrenzt, sondern variabel. Das kompliziert die erforderlichen
Berechnungsschritte. Die Energiehöhengleichung ist aber ebenfalls anwendbar und vereinfacht sich
zu folgender Form:
v12 2 g + z1 = v22 2 g + z2 + hv = H
Auch hier ist die Energiehöhe keine Konstante. Die Energiehöhe liegt im Abstand der
Geschwindigkeitshöhe über der freien Wasseroberfläche.
Aufgrund des zusätzlichen Freiheitsgrades bzw. des quadratischen Formelaufbaues kann der
Abfluß für eine vorgegebene Energiehöhe H mit zwei Wassertiefen h1 oder h2 erfolgen. Welche der
beiden Wassertiefen sich einstellt ist von äußeren Einflüssen abhängig.(z.B. vom Gefälle). Die
Gleichung weist ein Minimum Hmin auf. Die dazugehörige Wassertiefe wird als Grenztiefe
hgr bezeichnet.
Hmin ist die Energiehöhe, die mindestens erforderlich ist, um einen Abfluß Q durch eine bestimmte
Gerinneform abzuführen. Dabei stellt sich die Grenztiefe hgr und die Grenzgeschwindigkeit vgr ein.
Die allgemeine Grenzbedingung lautet:
Q 2 ⋅ bs g ⋅ A3 = 1
bs = Spiegelbreite
39
Handbuch zur Kleinwasserkraft
Für einen Rechteckquerschnitt vereinfachen sich die Formelzusammenhänge und es ergibt sich für
die Grenztiefe Folgendes:
H min = 1,5 ⋅ hgr
v gr =
g ⋅ hgr
Abflüsse, die mit h < hgr und damit mit v > vgr erfolgen werden als "schießend" bezeichnet, solche
mit h > hgr und V< Vgr als "strömend".
Während der Übergang von strömenden zum schießenden Abfluß kontinuierlich erfolgt, ist der
Übergang vom "Schießen" zum "Strömen" unstetig und mit der Ausbildung eines sogenannten "
Wechselsprunges" verbunden.
In der Regel erfolgt der Abfluß in offenen Gerinnen strömend.
Der Quotient aus der vorhandenen Geschwindigkeit v und der Grenzgeschwindigkeit wird als
FROUD'sche Zahl bezeichnet.
Fr < 1 strömender Abfluß
Fr > 1 schießender Abfluß
Fr = 1 Grenzfall
Je größer Fr wird, desto "stärker" schießt die Strömung und desto intensiver ist der Wechselsprung
beim Übergang in den strömenden Abfluß. Dabei wird überdurchschnittlich viel Energie
verbraucht.
7.4
Impulssatz
Nicht alle hydraulischen Fragestellungen können mit der Energiehöhengleichung beantwortet
werden. Der Impulssatz geht von folgender Überlegung aus:
Betrachtet man einen aus der Stromröhre "herausgeschnittenen" ortsfesten Flüssigkeitskörper, so
wirken auf ihn folgende Kräfte:
Im Schwerpunkt des Körpers das Eigengewicht G.
An den Außenflächen ggfls. Reibungskräfte T.
An den Schnittflächen:
die Druckkraft P = p.A
die Impulskraft J der in den Körper
eindringenden oder austretenden
Wassermengen.
40
Handbuch zur Kleinwasserkraft
Das Produkt aus Masse m und Geschwindigkeit v wird als Impuls bezeichnet.
Daraus ergeben sich folgende Impulskräfte:
(ρ = γ g
J 1 = v1 ⋅ ρ ⋅ Q
J 2 = v2 ⋅ ρ ⋅ Q
Damit ist es möglich, die Kräfteverhältnisse an den Grenzflächen eines Flüssigkeitskörpers zu
ermitteln, ohne dabei die Vorgänge im Inneren berücksichtigen zu müssen.
Die praktische Anwendung des Impulssatzes ergibt sich z.B. bei Querschnittsveränderungen oder
Krümmungen in Rohrleitungen. Diese verursachen Kräfte, die z.B. durch Widerlager aufgefangen
werden müssen.
7.5
Stützkraftsatz
Die Anwendung des Impulssatzes auf einen Abschnitt eines offenen Gerinnes stellt sich unter
Vernachlässigung der Reibungskraft T fiir die Breite b = 1 folgendermaßen dar:
Aus Gründen des Gleichgewichtes ist J1 + W1 = J2 + W2 = S
Die Kraft S wird Stützkraft genannt.
Allgemein gilt:
S = ρ ⋅ Q2 h + γ ⋅ h2 2
Die Beziehung findet vor allem bei der Berechnung des Wechselsprunges und des Schwall und
Sunkes Anwendung.
7.6
Strahldruck
Trifft ein freier Strahl auf ein Hindernis, so übt er auf dieses Hindernis eine Kraft aus. Diese kann
mit Hilfe des Impulssatzes berechnet werden.
W = J 1 ⋅ sin α = ρ ⋅ v1 ⋅ Q1 ⋅ sin α
Beträgt die Umlenkung 180° wird a = 90° und
der Strahldruck wird zur Summe beider Impulskräfte.
W(180°) = 2 J
(Anwendung bei der Peltonturbine)
41
Handbuch zur Kleinwasserkraft
7.7
Rohrströmung
7.7.1 Örtliche Verluste
Die Ursache örtlicher Verluste sind zum überwiegenden Teil Ablösungen der Strömung von den
Wandungen. Es bilden sich Strömungswirbel, deren Bildung Energie braucht.
Diese Art der Verluste ist direkt proportional der Strömungsgeschwindigkeit bzw. der
Geschwindigkeitshöhe v2/2g. Die Größe des Verlustes wird durch den Multiplikator ζ dargestellt.
Im Einzelnen gibt es folgende Verluste:
Einlaufverluste
Krümmungsverluste
42
Handbuch zur Kleinwasserkraft
Verluste bei Querschnittsänderung
Verluste bei Verschlußorganen
Rechenverluste
7.7.2 Kontinuierliche Verluste
Durch die äußere Reibung des strömenden Wassers an der Rohrwandung sowie durch eine Art
innere Reibung (Stoß- und Mischverluste) nimmt die Verlusthöhe hv entlang der Stromröhre
kontinuierlich zu.
Der Verlust ist direkt proportional der Länge des Rohres und indirekt proportional dem Querschnitt
des Rohres. Der Proportionalitätsfaktor wird λ genannt.
hv = λ d ⋅ L ⋅ v 2 2 g
Der Wert λ muß ermittelt werden. Er ist abhängig von der Reynold'schen Zahl und von der
Rauhigkeit (Sandrauhigkeit) des Rohres. Dieser Wert wird vom Rohrhersteller angegeben.
43
Handbuch zur Kleinwasserkraft
Das folgende Diagramm zeigt die Zusammenhänge.
7.8
Gerinneströmung
Die Gerinneströmung ist im Grundsatz ähnlich zu berechnen wie die Rohrströmung, wobei
folgende Annahmen getroffen werden:
Der Rohrdurchmesser d wird 4R (der hydraulische Radius R = A/U, U = der benetzte Umfang)
Die Ermittlung von λ kann wieder über ein Diagramm erfolgen.
Zum praktischen Gebrauch hat sich - obwohl fehlerbehaftet - die Fließformel von ManningStrickler durchgesetzt. Sie wurde rein empirisch ermittelt und lautet
v = k s ⋅ R 2 3 ⋅ I s1 2
v = mittlere Fließgeschwindigkeit
ks = Rauhigkeitsbeiwert
Is = Energieliniengefälle
R = hydraulischer Radius
Natürliche Flussbetten haben k-Werte zwischen 25 - 40
Künstliche Kanäle haben k-Werte zwischen 50 - 100
Es gibt Tabellen zur genauen Auswahl.
7.9
Überfallströmung
Unter Überfallströmung versteht man den Abflussvorgang, der sich einstellt, wenn das Wasser über
eine normalerweise horizontale Überfallkante eines Staubauwerkes zum Abfluß gelangt. Es gibt
drei Möglichkeiten der Anströmung:
• Rechtwinkelig (normales Überfallwehr)
• Radial (ringförmiger Überfall)
• Parallel zur Strömung (Streichwehr)
44
Handbuch zur Kleinwasserkraft
Die Überfallströmung wird durch die Formel von Poleni beschrieben.
Q = 2 3 ⋅ µ ⋅ b ⋅ (2 g ) ⋅ ho3 2
12
Die Überfallbeiwerte µ sind Formbeiwerte
Es gibt die Abflussform des vollkommenen und des unvollkommenen Überfalls. Im ersten Fall
erfolgt keine Beeinflussung der Überfallströmung von Unterwasser - im zweiten Fall schon.
7.10
Abfluß unter Schützen
Einen in der wasserbaulichen Praxis sehr häufigen Sonderfall bildet der sogenannte Grundstrahl.
Der Abfluß errechnet sich nach folgender Formel:
Q = c ⋅ µ ⋅ a ⋅ b ⋅ (2 g ⋅ ho )
12
c = Beiwert, der die Abflußart berücksichtigt
(vollkommen oder unvollkommen)
m = Abflussbeiwert
b = Breite des Grundstrahl
ho = Oberwasserstand
45
Handbuch zur Kleinwasserkraft
7.11
Abfluß aus Öffnungen
Bei der hydraulischen Betrachtung des Ausflusses
aus Öffnungen spielt das Verhältnis zwischen
der Höhe der Ausflussöffnung a und der mittleren
Druckhöhe h eine wesentliche Rolle.
Der Ausfluß ergibt sich formelmäßig als
Q = µ ⋅ A ⋅ (2 g ⋅ h )
12
7.12
Schwall und Sunk (Instationärer Fließvorgang)
Wird der Abfluß in einem offenen Gerinne plötzlich verändert - z.B. durch Öffnen oder Schließen
einer Wehranlage, kommt es infolge der Massenträgheit des Wassers zu einem kurzzeitigen
Anheben (Schwall) oder Absinken (Sunk) des Wasserspiegels flussauf oder flußab des
Verschlusses. Dabei unterscheidet man in
• Absperrschwall flussauf
• Absperrsunk flußab
• Öffnungsschwall flußab
• Öffnungssunk flußauf
7.13
Schleppspannung, Geschiebebewegung
Unter Geschiebe versteht man Feststoffe (meist Gestein), die durch den Fließvorgang an der
Gewässersohle rollend, gleitend oder hüpfend bewegt werden. Einflussfaktoren auf diese
Geschiebebewegung sind Wassertiefe und Gefälle.
Maßgebend ist die Schleppspannung an der Flusssohle. Diese ist formelmäßig folgendermaßen
definiert:
S = 10.000 ⋅ t ⋅ I (N m 2 )
t = Wassertiefe über der Sohle
I = Gefälle der Energielinie
Für den Wasserkraftplaner ist die Kenntnis der Geschiebeführung eines Flusses von großér
Bedeutung, da er mit konstruktiven Mitteln danach trachten muß, möglichst wenig oder gar kein
Geschiebe in den Turbinenzulauf gelangen zu lassen.
7.14
Schwebstoffe
Unter Schwebstoff versteht man jene Feststoffe, die zufolge Turbulenzen im Wasser in Schwebe
gehalten werden. Insbesondere bei Hochwässern ist nicht nur die Geschiebe- sondern auch die
Schwebstofführung eines Flusses im allgemeinen sehr hoch. Der Eintrag in die Turbine lässt sich
kaum vermeiden – allerdings ist auch das Beschädigungspotential wesentlich geringer.
46