2012-1ter_Termin - Helmut-Schmidt

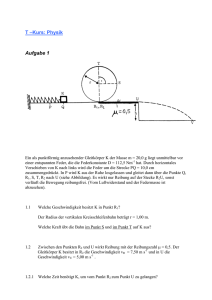
Helmut-Schmidt-Universität
Universität der Bundeswehr Hamburg
Fachbereich Elektrotechnik
Experimentalphysik und Materialwissenschaften
Univ.-Prof. Dr. D. Kip
Telefon: 6541 2457
Klausur Experimentalphysik (1. Termin)
Für Studierende des Studienganges Elektrotechnik (SJG 2011)
29. März 2012
(Bitte deutlich schreiben)
Name:
Matrikel-Nr.:
..............................
..............................
Vorname:
..............................
Aufgabe Titel
1
Zusammenstoß (10 Punkte)
2
Radreifen (10 Punkte)
3
Ballistisches Pendel (12 Punkte)
4
Wellen auf einer Saite (8 Punkte)
5
Interferenz (8 Punkte)
6
Geladene Kugeln (10 Punkte)
7
Satellit (12 Punkte)
8
Ladungen in elektromagnetischen Feldern (10 Punkte)
9
Auf und Ab (10 Punkte)
10
Wurf (10 Punkte)
Punktzahl
Gesamtpunktzahl (maximal 100)
Hiermit versichere ich, die Aufgaben der Klausur selbständig und ausschließlich unter Verwendung der zugelassenen Hilfsmittel bearbeitet zu haben.
Unterschrift: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Mit der Bekanntgabe der Klausurergebnisse in Kombination mit der Matrikel-Nummer (ohne
Namen) in Form eines Aushangs am schwarzen Brett und im Internet bin ich einverstanden.
(Wenn Sie dies nicht wünschen, streichen Sie den Satz bitte.)
Unterschrift: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Erlaubte Hilfsmittel: Schreibgeräte, nicht-programmierbare Taschenrechner
Bitte beachten Sie:
Tragen Sie Ihre Lösungen in die dafür vorgesehenen Kästchen ein. Sind diese zu
klein, verwenden Sie bitte die Rückseiten.
Wenn nach dem allgemeinen Ausdruck gefragt ist, sollten vektorielle Größen als
solche zu erkennen sein.
Physikalische Konstanten und Zahlenwerte
Erdbeschleunigung
g = 9, 81 m/s2
Erdmasse
Me = 5, 98 · 1024 kg
Erdradius
Re = 6370 km
Gravitationskonstante
G = 6, 67 · 10−11 m3 /(kg s2 )
Dielektrizitätskonstante
ε0 = 8, 85 · 10−12 As/(Vm)
Elementarladung
e = 1, 602 · 10−19 As
magnetische Feldkonstante
µ0 = 4π · 10−7 Vs/(Am)
2
1. Zusammenstoß
Ein unbeladener Wagon der Masse m1 = 20 t fährt mit einer Geschwindigkeit von v1 =
36 km/h auf einen zweiten Wagon mit der Masse m2 = 5·m1 = 100 t auf, der sich mit einer
Geschwindigkeit von v2 = v1 /5 = 7, 2 km/h nähert. Die Puffer an beiden Wagons können
als Feder mit der Federkonstante D angesehen werden. Es soll angenommen werden, dass
der Zusammenstoß elastisch verläuft, d.h. es treten keine Energieverluste aufgrund von
Reibung oder dauerhaften Verformungen auf. Nutzen Sie die für diesen Fall geltenden
Erhaltungssätze.
a) Im Moment größter Annäherung haben beide Wagen die gleiche Geschwindigkeit. Wie
groß ist diese? Wie viel Energie steckt zu diesem Zeitpunkt in den Federn? Gesucht
sind Ausdruck und Zahlenwert. (4 Punkte)
3
b) Wie stark werden die Federn eingedrückt, wenn die Federkonstante D = 15 kN/cm
ist? Gesucht ist der Zahlenwert. (2 Punkte)
c) Geben Sie die Ausdrücke und Zahlenwerte für die Geschwindigkeit der beiden Wagons
nach dem Zusammenstoß, d. h. wenn sie sich voneinander gelöst haben, an.
(4 Punkte)
4
2. Radreifen
Das Rad eines Zuges besteht aus einem Radkörper mit dem Radius RN = 1 m und
einem umschließenden Radreifen mit dem äußeren Radius RM = 1, 125 m. Radkörper
und Radreifen bestehen aus unterschiedlichen Materialien. Für den Radkörper wurde
Holz mit einer Dichte von % = 6, 7 g/cm3 verwendet. Der Radreifen besteht aus Stahl mit
einer Dichte von % = 7.91 g/cm3 . Das Rad sei 9, 5 cm dick.
a) Geben Sie die allgemeine Definition des Trägheitsmoments einer kontinuierlichen Massenverteilung in der Integralform an. (1 Punkt)
b) Berechnen Sie ausgehend von der allgemeinen Definition aus a) durch Integration das
Trägheitsmoment des gesamten Rades. Gesucht sind Ausdruck und Zahlenwert.
(4 Punkte)
5
d) Der Zug bremst mit einer zeitabhängigen Verzögerung der Form a(t) = a0 − kt und
kommt nach der Zeit τ zum Stehen. Wie lange muss er bremsen, wenn er eine
Anfangsgeschwindigkeit von v0 = 86, 4 km/h hatte und wenn gilt a0 = 1 m/s2 bzw.
k = 1/50m/s3 ? Gesucht ist der Zahlenwert. (3 Punkte)
c) Wie viele Umdrehungen führt das Rad während des Bremsvorganges aus? Gesucht ist
der Zahlenwert. (2 Punkte)
6
3. Ballistisches Pendel
Ein dünner langer Stab der Länge L = 1 m mit einer Masse von M = 10 kg ist an
seinem oberen Ende drehbar aufgehängt. Eine Kugel der Masse m1 = 18, 6 g wird mit
der Geschwindigkeit v in das untere Ende des Stabes geschossen und bleibt stecken. Der
anschließend beobachtete maximale Auslenkwinkel des Stabes ist α = 25◦ .
a) Das Trägheitsmoment des Stabes um die Achse durch seinen Mittelpunkt ist Js =
M L2 /12. Wie groß ist nach dem Steinerschen Satz das Trägheitsmoment im hier
vorliegenden Fall? Geben Sie den Zahlenwert an. (2 Punkte)
b) Geben Sie den Ausdruck für den Drehimpuls der Kugel bezogen auf die Drehachse
des Stabes kurz bevor die Kugel einschlägt an? (2 Punkte)
c) Welcher Ausdruck ergibt sich für die Winkelgeschwindigkeit von Stab und Kugel direkt
nach dem Einschlag? Welcher Ausdruck ergibt sich für die zugehörige Rotationsenergie? (3 Punkte)
7
d) Geben Sie den Ausdruck für die potentielle Energie des Stabes an, wenn dieser um
den Winkel α ausgelenkt ist. (2 Punkte)
e) Nutzen Sie die Ergebnisse aus c) und d), um den Zahlenwert für die Geschwindigkeit
der Kugel vor dem Einschlag zu ermitteln. (3 Punkte)
8
4. Wellen auf einer Saite
Eine 4 m lange Saite mit einer Gesamtmasse von m = 9, 81 g werde durch eine verschiebbare Halterung starr fixiert und durch zwei herabhängende Gewichtstücke der Masse
m1 = 76, 8 kg und m2 auf der jeweils anderen Seite gespannt. Der Abstand zwischen den
beiden Umlenkrollen sei ` = 3 m. Ein Beobachter verschiebt die Halterung soweit, bis er
für die Frequenzen der Grundschwingungen der beiden Abschnitte `1 und `2 den gleichen
Wert erhält. Für die Strecke `2 ergibt sich so ein Wert von 1 m.
a) Geben Sie den allgemeinen Ausdruck für die Ausbreitungsgeschwindigkeit von Wellen
auf einer gespannten Saite an? (2 Punkte)
b) Welcher Zahlenwert ergibt sich für die Wellenlänge der Grundwelle auf der Saite `2 ?
(2 Punkte)
c) Welcher Wert ergibt sich für die Frequenz der Grundwelle? (2 Punkte)
9
d) Welcher Zahlenwert ergibt sich für die Masse m2 ? (2 Punkte)
10
5. Interferenz
Die Lautsprecher L1 und L2 sind im Abstand d = 7, 5 m voneinander angeordnet.
Beide strahlen phasengleich einen Ton der Frequenz f ab. Ein Beobachter startet am
Lautsprecher L2 und bewegt sich senkrecht zur Verbindungslinie L2 L1 . An den Punkten
y1 = −0, 3848 m, y2 = −1, 224 m und y3 = −2, 1875 m hat die vom Beobachter gemessene
Leistung Minima.
a) Geben Sie den Ausdruck für die Weglängendifferenz der beiden emittierten Wellen am
Ort des Beobachters an. (2 Punkte)
b) Lautsprecher L2 hat eine Leistung von P2 = 20 W, die homogen in den Raum abgestrahlt wird. Welche Leistung hat Lautsprecher L1 , wenn der Beobachter am Punkt
y3 eine vollständige Auslöschung misst? Gesucht ist der Zahlenwert. (2 Punkte)
11
c) Nutzen Sie den Ausdruck aus a), um die Zahlenwerte der Wellenlänge und der Frequenz
der emittierten Schallwellen zu ermitteln. Nehmen Sie für die Schallgeschwindigkeit
vs = 330 m/s an. (4 Punkte)
12
6. Geladene Kugeln
Zwei Kugeln mit gleicher Masse und gleicher Ladung seien entsprechend der Abbildung angeordnet. Eine der Kugeln sei am Ende eines Stabes fixiert. Die andere sei an einem masselosen Faden
befestigt.
a) Geben Sie den allgemeinen Ausdruck für die Coulombkraft zwischen zwei Ladungen
q im Abstand s an. (1 Punkt)
q
b) Zeigen Sie, dass sich im vorliegenden Fall für den Abstand s = R 2(1 − cos(α))
ergibt. (2 Punkte)
Legt man die fixierte Kugel an den Punkt (0, −R) des Koordinatensystems, kann die Position der Kugel am Faden durch den Vektor f~ = R(sin(α); − cos(α)) angegeben werden.
Dieser Vektor gibt zugleich die Richtung des Fadens vor.
c) Ermitteln Sie den Ausdruck für den Vektor ~s, der die Richtung der Coulombkraft
angibt. (1 Punkt)
13
d) Geben Sie einen Ausdruck für den Winkel δ zwischen den Vektoren f~ und ~s an.
(2 Punkte)
e) Welcher Ausdruck ergibt sich für die Komponente der Coulombkraft, die senkrecht
auf f~ steht? (1 Punkt)
f ) Geben Sie den Ausdruck für die Komponenten der Gewichtskraft an, die auf die Kugel
am Faden wirkt und die gleichfalls senkrecht auf f~ steht. (1 Punkt)
g) Setzen Sie die Beträge der beiden Kraftkomponenten aus e) und f) gleich und geben
Sie die Ladung q auf den Kugeln als Funktion ihrer Masse und des Winkels α an.
Welcher Zahlenwert ergibt sich für m = 10 mg und α = 20◦ ? (2 Punkte)
14
7. Satellit
Ein Satellit der Masse ms soll in eine Umlaufbahn mit dem Radius Rs geschossen werden.
In der Umlaufbahn wirken auf den Satelliten zwei Kräfte: die Gravitationskraft FG der
Erde und die Zentrifugalkraft FZ .
a) Geben Sie allgemein die Gravitationskraft zwischen zwei punktförmigen Massen im
Abstand r an. (1 Punkt)
b) Geben Sie den Ausdruck für die Zentrifugalkraft an, die auf den Satelliten wirkt.
(1 Punkt)
c) Leiten Sie mit Hilfe der Ausdrücke aus a) und b) die Formel für die Bahngeschwindigkeit des Satelliten ab. (3 Punkte)
15
d) Geben Sie die allgemeine Definition der Arbeit bei einer ortsabhängigen Kraft an.
(1 Punkt)
e) Berechnen Sie den Betrag der Arbeit, die notwendig ist, um den Satelliten von der
Erdoberfläche in die Umlaufbahn zu heben. (3 Punkte)
f ) Berechnen Sie den Wert der Abschussgeschwindigkeit v0 und des Winkels zur Horizontalen, die notwendig sind, um den Satelliten in seine Umlaufbahn zu schießen. Der
Satellit habe eine Masse von m = 1000 kg und soll eine Umlaufbahn in der Höhe
Rs = Re + 4000 km erreichen. (3 Punkte)
16
8. Ladungen in elektromagnetischen Feldern
Ein Elektron tritt mit der Geschwindigkeit ~v in das Feld eines Kondensators ein.
a) Geben Sie den allgemeinen Ausdruck für das elektrische Feld in einem Kondensator
an, an dem die Spannung U anliegt und dessen Platten den Abstand d haben.
(1 Punkt)
b) Zeichnen Sie in der Skizze die Richtung der Feldlinien des elektrisches Feldes im Kondensator ein. (1 Punkt)
c) Geben Sie die Kraft an, die auf das Elektron im elektrischen Feld des Kondensators
wirkt. (1 Punkt)
d) Wo und unter welchem Winkel verlässt das Elektron den Kondensator? (2 Punkte)
17
Ein Elektron tritt mit der Geschwindigkeit ~v in ein räumlich begrenztes Magnetfeld ein.
e) Geben Sie den allgemeinen Ausdruck für die Kraft an, die auf das Elektron im Magnetfeld wirkt. (1 Punkt)
f ) Zeichnen Sie in der Skizze die Richtung der Kraft ein, die auf das Elektron wirkt.
(1 Punkt)
g) Wo und unter welchem Winkel verlässt das Elektron das Magnetfeld? (2 Punkte)
h) Welcher Wert ergibt sich für das Verhältnis der Feldstärken von E und B für den
Fall, dass die Austrittswinkel in d) und g) gleich sind? ( Nehmen Sie an, dass die
Ablenkwinkel klein sind und näherungsweise gilt sin(α) ≈ tan(α).) (1 Punkt)
18
9. Auf und Ab
Ein Gegenstand der Masse M = 2 kg ist am oberen Ende einer am Boden verankerten
Feder mit der Federkonstante D befestigt. Die entspannte Feder ist h = 80 cm lang; mit
Gewicht ergibt sich eine Gleichgewichtslage von h0 = 70 cm. Der ruhenden Masse werde
in der Gleichgewichtslage (z.B. durch einen kurzen Hammerschlag) eine Geschwindigkeit
von 0, 36 m/s nach unten verliehen.
a) Stellen Sie die Bewegungsgleichung für die Masse M auf, wenn diese aus der Gleichgewichtslage ausgelenkt wird. (1 Punkt)
b) Geben Sie die allgemeine Lösung dieser Gleichung an. (2 Punkte)
c) Geben Sie die unter den hier vorliegenden Randbedingungen gültige Lösung an.
(2 Punkte)
19
d) Ermitteln Sie anhand der gegebenen Größen die Zahlenwerte für Amplitude und Frequenz der Schwingung. (3 Punkte)
e) Welche Anfangsgeschwindigkeit muss der Masse verliehen werden, damit die Feder
vollständig entspannt, wenn die Masse ihre maximale Entfernung vom Boden erreicht? Gesucht ist der Zahlenwert. (2 Punkte)
20
10. Wurf
Zwei Kinder möchten ein Kunststück vorführen. Eines der Kinder steht auf dem Dach
eines Gebäudes und lässt einen Ball fallen. Gleichzeitig soll das anderes Kind seinen Ball
so werfen, dass sich beide Bälle in der Luft treffen. Das zweite Kind kann den Ball mit
der Geschwindigkeit v0 werfen.
a) Stellen Sie Gleichungen für die Bewegung in x- und y-Richtung für beide Bälle auf.
(2 Punkte)
b) Geben Sie den Ausdruck für den Winkel an, unter dem das zweite Kind den Ball
werfen muss, damit sich die Bälle treffen. (2 Punkte)
21
c) Geben Sie den Ausdruck für die Höhe an, in der sich die Bälle treffen. (2 Punkte)
d) Berechnen Sie die Zahlenwerte für die Höhe des Treffpunktes und den Winkel, unter
dem das zweite Kind werfen muss, unter der Annahme dass v0 = 15 m/s, h0 = 1, 3 m,
h = 5 m und s0 = 10 m sind. (2 Punkte)
e) Welcher Zahlenwert ergibt sich für v0 , wenn die Bälle sich treffen sollen, kurz bevor
sie den Boden erreichen? (2 Punkte)
22