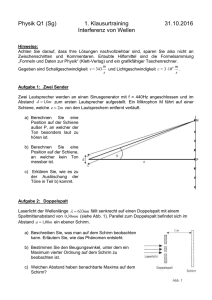
1 1. Klausur 13/I Beugung und Interferenz am Gitter

1
1. Klausur 13/I
Q2PHG1 Ernesti
Lichtbrechung und -beugung
26. Oktober 2012
•
•
•
Kommentieren Sie Ihre Lösungen! (Erläuterungen, Begründungen, Folgerungen)
Rechnen Sie in SI-Einheiten (kg, m, s etc.)!
Überprüfen Sie die physikalischen Einheiten in Ihren Rechenschritten und Lösungen! (Vor allem bei längeren Rechenwegen!)
Erlaubte Hilfsmittel: Taschenrechner, Formelsammlung, Schreibutensilien
Lichtbrechung Beim Übergang zwischen zwei transparenten Medien wird ein Teil des Lichtes gebrochen. Dieser Effekt
lässt sich mit dem Huygensschen Prinzip und der Annahme, dass Licht in unterschiedlichen Medien auch unterschiedliche
Ausbreitungsgeschwindigkeiten hat, erklären. Das Gehirn des Beobachters „kennt“ allerdings nur geradlinige Lichtausbreitung
und verlängert den ankommenden gebrochenen Lichtstrahl geradlinig zu seinem virtuellen Ursprungsort. Dadurch entstehen
einige interessante optische Eindrücke.
1.1.
a) Aus dem Vakuum trifft ein Lichtstrahl unter einem Winkel von 30° zum Lot auf eine 10cm dicke
Glasscheibe mit dem Brechungsindex n=1.5.
Fertigen Sie eine Skizze des Strahlengangs an.
b) Um wieviele cm ist der Strahl, der aus der Glasscheibe wieder austritt, gegenüber dem Einfallsstrahl
parallel verschoben?
c) Gibt es einen Winkel, bei dem der Lichtstrahl an der Grenzfläche Vakuum/Licht totalreflektiert wird und
daher nicht in das Glas eindringen kann? Begründen Sie Ihre Antwort!
1.2.
In ein Wasserbecken von 2 m Tiefe wird ein Pfahl gerammt, der 50 cm
aus dem Wasser herausragt. Wie lang ist der Schatten des Pfahls auf
dem Grund des Wasserbeckens, wenn die Sonnenstrahlen unter einem
Winkel von 60° zur Wasseroberfläche einfallen?
60°
Beugung und Interferenz am Gitter Eine wichtige Eigenschaft von Wellen ist, dass sie sich unter gewissen
Bedingungen nicht geradlinig ausbreiten (Beugung). Zudem kann es zur Verstärkung und Auslöschung der Intensitäten bei der
Überlagerung von Wellen kommen (konstruktive und destruktive Interferenz). Dass Licht beim Durchscheinen eines
Doppelspaltes oder eines optischen Gitters diese Eigenschaften ebenfalls zeigt, weist auf seinen Wellencharakter hin.
Auf ein optisches Gitter mit der Gitterkonstante g =4,00⋅10−6 m fällt Licht der Wellenlänge λ=694 nm senkrecht
ein. Das Interferenzbild wird auf einem e=2,00m entfernten ebenen Schirm beobachtet, der parallel zum Gitter
steht. Auf dem Schirm entstehen n Helligkeitsmaxima im Abstand an jeweils links und rechts von der optischen
Achse (n = 1,2,3,...).
2.1.
Fertigen Sie eine Skizze des Versuches an und leiten Sie den Zusammenhang zwischen an , g , e und
λ her.
2.2.
Berechnen Sie den Abstand der auf dem Schirm sichtbaren Helligkeitsmaxima 1. Ordnung voneinander.
2.3.
Bis zur wievielten Ordnung können theoretisch Helligkeitsmaxima auftreten?
2.4.
Weisen Sie rechnerisch nach, dass die Spektren 2. und 3. Ordnung einander überlappen, wenn
sichtbares Licht aus dem Wellenlängenintervall zwischen 400 nm und 750 nm benutzt wird!