Arbeitsblatt 3: Interferenz am optischen Gitter
Werbung
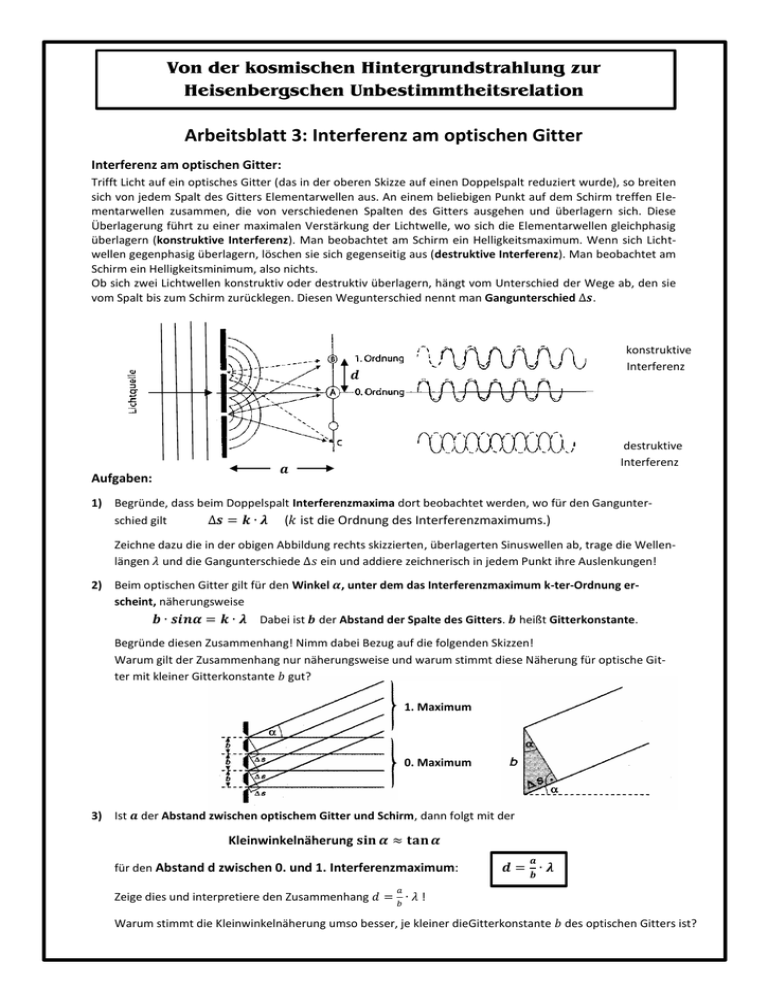
Von der kosmischen Hintergrundstrahlung zur Heisenbergschen Unbestimmtheitsrelation Arbeitsblatt 3: Interferenz am optischen Gitter Interferenz am optischen Gitter: Trifft Licht auf ein optisches Gitter (das in der oberen Skizze auf einen Doppelspalt reduziert wurde), so breiten sich von jedem Spalt des Gitters Elementarwellen aus. An einem beliebigen Punkt auf dem Schirm treffen Elementarwellen zusammen, die von verschiedenen Spalten des Gitters ausgehen und überlagern sich. Diese Überlagerung führt zu einer maximalen Verstärkung der Lichtwelle, wo sich die Elementarwellen gleichphasig überlagern (konstruktive Interferenz). Man beobachtet am Schirm ein Helligkeitsmaximum. Wenn sich Lichtwellen gegenphasig überlagern, löschen sie sich gegenseitig aus (destruktive Interferenz). Man beobachtet am Schirm ein Helligkeitsminimum, also nichts. Ob sich zwei Lichtwellen konstruktiv oder destruktiv überlagern, hängt vom Unterschied der Wege ab, den sie vom Spalt bis zum Schirm zurücklegen. Diesen Wegunterschied nennt man Gangunterschied ∆𝒔. Licht konstruktive Interferenz 𝒅 Aufgaben: destruktive Interferenz 𝒂 1) Begründe, dass beim Doppelspalt Interferenzmaxima dort beobachtet werden, wo für den Gangunterschied gilt ∆𝒔 = 𝒌 ∙ 𝝀 (𝑘 ist die Ordnung des Interferenzmaximums.) Zeichne dazu die in der obigen Abbildung rechts skizzierten, überlagerten Sinuswellen ab, trage die Wellenlängen 𝜆 und die Gangunterschiede ∆𝑠 ein und addiere zeichnerisch in jedem Punkt ihre Auslenkungen! 2) Beim optischen Gitter gilt für den Winkel 𝜶, unter dem das Interferenzmaximum k-ter-Ordnung erscheint, näherungsweise 𝒃 ∙ 𝒔𝒊𝒏𝜶 = 𝒌 ∙ 𝝀 Dabei ist 𝒃 der Abstand der Spalte des Gitters. 𝒃 heißt Gitterkonstante. Begründe diesen Zusammenhang! Nimm dabei Bezug auf die folgenden Skizzen! Warum gilt der Zusammenhang nur näherungsweise und warum stimmt diese Näherung für optische Gitter mit kleiner Gitterkonstante 𝑏 gut? 1. Maximum 0. Maximum 3) Ist 𝒂 der Abstand zwischen optischem Gitter und Schirm, dann folgt mit der Kleinwinkelnäherung 𝐬𝐢𝐧 𝜶 ≈ 𝐭𝐚𝐧 𝜶 für den Abstand d zwischen 0. und 1. Interferenzmaximum: 𝒂 𝒅=𝒃∙𝝀 𝑎 Zeige dies und interpretiere den Zusammenhang 𝑑 = ∙ 𝜆 ! 𝑏 Warum stimmt die Kleinwinkelnäherung umso besser, je kleiner dieGitterkonstante 𝑏 des optischen Gitters ist?











