„Würfeln“ mit dem Taschenrechner

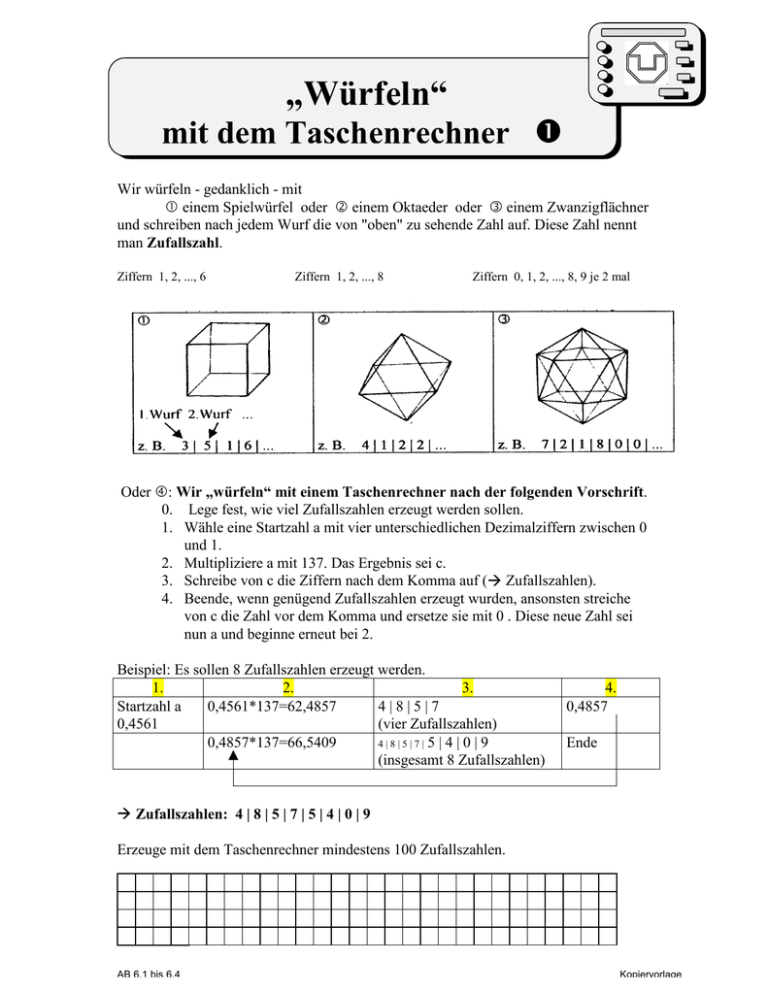
„Würfeln“
mit dem Taschenrechner
Wir würfeln - gedanklich - mit
einem Spielwürfel oder
einem Oktaeder oder
einem Zwanzigflächner
und schreiben nach jedem Wurf die von "oben" zu sehende Zahl auf. Diese Zahl nennt
man Zufallszahl.
Ziffern 1, 2, ..., 6
Oder
Ziffern 1, 2, ..., 8
Ziffern 0, 1, 2, ..., 8, 9 je 2 mal
: Wir „würfeln“ mit einem Taschenrechner nach der folgenden Vorschrift.
0. Lege fest, wie viel Zufallszahlen erzeugt werden sollen.
1. Wähle eine Startzahl a mit vier unterschiedlichen Dezimalziffern zwischen 0
und 1.
2. Multipliziere a mit 137. Das Ergebnis sei c.
3. Schreibe von c die Ziffern nach dem Komma auf ( Zufallszahlen).
4. Beende, wenn genügend Zufallszahlen erzeugt wurden, ansonsten streiche
von c die Zahl vor dem Komma und ersetze sie mit 0 . Diese neue Zahl sei
nun a und beginne erneut bei 2.
Beispiel: Es sollen 8 Zufallszahlen erzeugt werden.
1.
2.
3.
Startzahl a
0,4561*137=62,4857
4|8|5|7
0,4561
(vier Zufallszahlen)
0,4857*137=66,5409
4|8|5|7| 5 | 4 | 0 | 9
(insgesamt 8 Zufallszahlen)
4.
0,4857
Ende
Zufallszahlen: 4 | 8 | 5 | 7 | 5 | 4 | 0 | 9
Erzeuge mit dem Taschenrechner mindestens 100 Zufallszahlen.
AB 6.1 bis 6.4
Kopiervorlage
„Wie viele Sticker muss ich
kaufen, um ...“
Auftrag 1
Wie viele Zufallszahlen muss man mit dem Taschenrechner vermutlich
erzeugen (siehe ), um jede der Zahlen 0, 1, 2, 3, ..., 9 wenigstens einmal
dabei zu haben?
Wenn jede der Zahlen 0, 1, 2, 3 ..., 9 wenigstens einmal dabei ist, dann hat man
eine vollständige Serie.
• Schätze die Anzahl der Zahlen, die man durchschnittlich für eine vollständige Serie aufschreiben muss.
--------------------• Überprüfe deinen Schätzwert mit den Zufallszahlen auf dem Arbeitsblatt . Zähle - wenn möglich – mehrere vollständige Serien aus und
schreibe die jeweilige Anzahl der Zufallszahlen auf (2. Spalte Tabelle).
Du kannst beginnen, wo du möchtest. Zähle immer fortlaufend.
• Berechne das arithmetische Mittel der Anzahlen (2. Spalte Tabelle)
• Übernehme die Werte deiner Mitschüler und berechne erneut das
arithmetische Mittel (3. Spalte Tabelle).
eigenes Experiment
Experimente der Mitschüler
Anzahl der Zufallszahlen für vollständige Serie
arithmetisches Mittel
•
Was hat das Experiment mit „Sticker“ zu tun ?
Auftrag 2
Untersuche die Häufigkeit der Zufallszahlen 0, 1, 2, ..., 8 und 9 aus dem
eigenen Experiment oder den Experimenten der Mitschüler. Fertige dazuein geeignetes Diagramm an. Was stellst du fest? Gilt das auch für die
Sticker?
AB 6.1 bis 6.4
Kopiervorlage
Mehr als eine Lösung
1
Suche für a, b, c ... Zahlen, so dass gilt:
a) a b = 84
c) 3 c + 5 d = 53
e) 9 e + 25 f = 122
b) g h = 442
d) 9 i + 5 j = 222
f) m : n - 12 = 0
2
Wenn zum 10fachen einer Zahl das 6fache einer anderen Zahl addiert wird,
so erhält man 72.
Welche Zahlen sind das ?
3
272 DM sollen an zwei Gruppen mit 8 und 10 Schülern aufgeteilt werden,
wobei die Schüler einer Gruppe jeweils den gleichen Betrag erhalten. Welche Möglichkeiten gibt es?
4
Für drei Klassen sollen als Preise Bücher und Spiele für insgesamt 100
DM gekauft werden. Es sollen mehr Spiele als Bücher dabei sein. Ein
Buch kostet 6 DM, ein Spiel 4 DM.
5
Auf einem Bauernhof mit Hühnern und Schafen werden 76 Beine und 33
Köpfe gezählt. Wie viel Hühner und wie viel Schafe sind es ?
6
Ein Rechteck soll mit 120 Einheitsquadraten ausgelegt werden. Gib die
Anzahl der Einheitsquadrate an, die für Länge und Breite solcher Rechtekke möglich sind.
AB 6.1 bis 6.4
Kopiervorlage
Teilbar durch 7 ?
Teilerdiagramme
Eine natürliche Zahl a ist durch 7 teilbar, wenn ihr Querwert
durch 7 teilbar ist.
Der Querwert (QW) – eine frei gewählte Bezeichnung – ist wie folgt zu berechnen:
• Erste Ziffer von a mal 3 plus nächste Ziffer von a
• Ergebnis mal 3 plus nächste Ziffer von a usw. bis es keine nächste Ziffer von a
mehr gibt.
• Wenn dir der QW zu groß ist, dann berechne seinen QW nach der gleichen Vorschrift usw.
Beispiel :
a= 126
7|126 ?
Bestimmen des QW:
*3+6
*3+2
21
5
1
7|21 damit auch 7|126
Sind die folgenden Zahlen durch 7 teilbar?
2 135 ; 3 528 ; 1 260 ; 54 979 ; 1 003 ; 18 144 ; 8 065 und 54 971
Überprüfe deine Aussage jeweils mit dem Taschenrechner.
Teilerdiagramme
Mit Hilfe von Teilerdiagrammen kann man die Teiler einer Zahl zweckmäßig und
übersichtlich anordnen. Erkunde das Beispiel „Teiler von 36“ selbständig.
Teiler von 36
Teiler von 30
1
1
3
4
9
Teiler von 70
1
Teiler von 196
1
2
6
4
„Immer abwärts!“
AB 6.1 bis 6.4
Kopiervorlage