Berufs-/Fachmittelschulen Olten 1 Solothurn Fach: Mathematik

Berufs-/Fachmittelschulen
Olten 1 Solothurn
Fach: Mathematik Geometrie
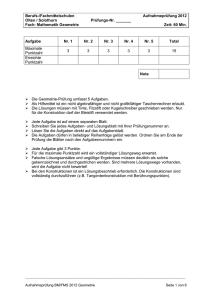
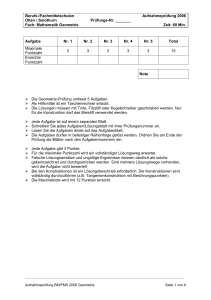
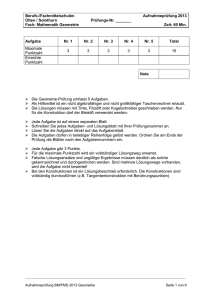
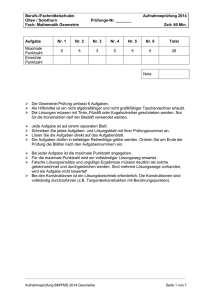
Aufgabe
Maximale
Punl<lzahl
Erreichte
Punl<tzah/
Aufnahmeprüfung 2012
Prüfungs-Nr. _ __
Zeit: 60 Min.
Nr.1
Nr.2
Nr. 3
Nr. 4
Nr. 5
Total
3
3
3
3
3
15
1 Note
}:>
}:>
}:>
Die Geometrie-Prüfung umfasst 5 Aufgaben.
Ais Hilfsmit!e/ ist ein nicht a/gebrafahiger und nicht grafikfahiger Taschenrechner erlaubt.
Die Lèisungen müssen mit Tinte, Filzstift oder l<uge/schreiber geschrieben werden. Nur
für die l<onstruktion darf der 8/eistift verwendet werden.
}:>
}:>
}:>
}:>
Jede Aufgabe ist auf einem separaten Blatt.
Schreiben Sie jedes Aufgaben- und Losungsb/att mit lhrer Prüfungsnummer an.
Lèisen Sie die Aufgaben direl<t auf das Aufgabenblatt.
Die Aufgaben dürfen in be/iebiger Reihenfolge ge/ost werden. Ordnen Sie am Ende der
Prüfung die B/atter nach den Aufgabennummern ein.
Je de Aufgabe gibt 3 Punl<te.
Für die maximale Punktzahl wird ein vol/standiger Lèisungsweg erwa1tet.
J:> Falsche Lèisungsansatze und ungültige Ergebnisse müssen deut/ich ais so/che
gekennzeichnet und durchgestrichen werden. Sind mehrere Lèisungswege vorhanden,
wird die Aufgabe nicht bewertet!
}:> Bei den l<onstruktionen ist ein Liisungsbeschrieb eJforder/ich. Die l<onstruktionen sind
vol/standig durchzuführen (z.B. Tangentenkonstrul<!ion mit Berührungspunkten).
}:>
}:>
Aufnahmeprüfung BM/FMS 2012 Geometrie
Seite 1 von 6
Aufnahmeprüfung 2012
Berufs-/Fachmittelschulen
Olten/ Solothurn
Fach: Mathematik Geometrie
Prüfungs-Nr. _ __
Zeit: 60 Min.
Aufgabe 1
a)
Gegeben ist der Halbkreis mit Mittelpunkt M. Die Winkel messen a"' 49o und
Berechnen Sie den Winkel y.
, .
!
6 ~;~~f.'~L~···i •~.:~kt;
·
·
~
·
'
4
.
.~·.,....+.·' ::::::,·
"f. •
i
'
~
•
T
(f····-
!.
, .
·--- -·-r···
---.l ....... _.i..,
:
,---
;......J
.
)
--.
-----.,
! ____ ) -----~ _____ )
r··-'''''',': ••••••'••·••••·-,·,,·• .....
:
,
------~
------.
:
j_
..·.•·.·_•·.·_:!.'. _____
.
i
·····! ······! ······!
:
:
.....L..... L.....i _____ .i
b)
l
,
,
. _____ , ... ...]
• ····:
)
' ..
~.~,
i
•
"
------:
' :.· : ;· • .,: '.: :.
t
!.:
,
.......,! ..... .:..
-----1
------~-- ....L. --:
'
i,
i
......:.
....
:.i
'
! ! i
i l i
:.'
:'.•
:. .
.••••••.:
i
l
!~·'.8.
'
1
L...... L..... l
1
i
;
:
l
l
• -----ï -----.
:
:
-----~ -----~ ----~
:
,
..•. ;, ... ,,!,, •
,,~~-.
.
A
1
••••••<••••
:
,
. ----··:
,
i
----: -----1
... -.i .... ..l
' ••••••,1
0
.. )
1
l
••Î, ••••••i,•••• ••f,'
:.;
! ..... _~.·
1 ..... :........ j
=
:
1
L
------~ . .) -·····: ......L.. _j ------~ ......, -----~ ...../ ......] ------1j
••••••f. ••••••}. ••••••:. ••••••< •····-,
,
,l ,,,,,!'i .
!
!
1
:
!
1
!
,
73°.
••••••Î,
.
••••••f, ••••••:
:
'
·····f
!
.
. ····+ ····!···· --!---- · ;,: ------t--------} ·····+ .... ) ······i······l······! ------~ · · · :.:· i i . __ ..j_ ·----f ------i---··r i ____ ,__ ----! ------1 ------! ------1 ___ .) ..... ! ...... ! ------! ------~ - - - ~ ------~ :::].-j ------l- __..J_
, -----1
.-.... ·.·_7,' ·····t ····l
.
!
.
.
'
-----} ······l
' _ -----~---· ______,________, ______,________, ......:. , .....L.......l ......L.......t ..... ~ ·····- ·····' ............J ......L......l .....1
······i ·····+
L_ _ J . . ..! ...... ; ------i ------1
:
...
'
t
i
~.~~..
;
..... L.
-----,
------! ······:
l.
t; {:J
__________
, . . .:
,
·····(··
,
: ...... :
.·.·_-_.._·..r.
M:
~"'
'
::J _ _ _
,
~
Die gezeichnete Gerade ist eine Tangente. Berechnen Sie allgemein den Winkel
dem gegebenen Winkel a.
aus
:!-p
2
Tangente
:
l :
i
:
:
:
:
:
:
:
:
:
~;~~1:~Ftt.c19r1J,;(2
...[
>:.,
..... ..i:····
..... :'. .....l .....
!.
:
:: .........:..
L.. .....l... ....J:. ..... t:. ......l:. ·····-···...
·.·.·_:.·_·
:
... -'-....
•
; i48~~+~b4J.4~-~~
1 $4~r.:f : 1/(
+z : ... . )
·····-~--------Ï---····-~·-····)........ 1........ ;........;........)........~...... )
.... ;
.
..... t.• .....1,: , ,""""""i:i :: ,
1
,'.• ·.·..... ·.--.·.-.,'........ ..·.··-·. •.v.·.·
.... ·.·.,:./:J
..-.. ·.·.·.·.·.'.cv.·_·_·
. __.._·_·_·,.·-:.._·_·_·_·_·
:•
__ ..:,:
.
•
i------r- ... ..t -----! ------i
. .
:
:
v.·_·.·
.'....
•
.
. .
;
i
:2: ' , ~z
1 ~
------i ----+ -----~ ______. --·. .
.
•
.
::
•
.
:
.
.
1!
:
l!.
, -'
l
.: · · r ,
i
'······•'····
~
1
l
i
,
,
..l
......L
···---~
i
....
••
.
.
4!
..r._:
.)
•
:!,
......
,
...
!
.
,
,
_
H
·.·.·_·_-_b_·
"-
-.
, ··· ··[
.
.
.
.
···--<· ..... ;
......~ ......, .............
.. : ..... ~ .... .!......! ......! ......~ ··----~ ......~ .....;....... .:........ :........: ....... ' .....! ' . . L. . .J.....L......L..... J
AufnahmeprUfung BM/FMS 2012 Geometrie
··•'····
'
,l
, ...... •..•.......••
·
'
p
..... :......... :......... .: ........ :'........:........ ~.
i ......; ...... ; ......;... ~ ......·. ····-~.:···A.:· ····: ······:· ·····,·'.
i
i
i
i
1
~
----1--.. --~ ------i ......, ......} ......1. -----1 ------! ------[ ------i ------} ------t:=i==i=i==i=-----i
..J ......o_.. .
......( ... -•·.············Î'
.
.· •• •••.•..... ·.............................
.·,
;..........·.-r,,,· ·.·.·..·.·.·.·!,,·· ..... ~ ...... 1 ......J
.....
i
i...... ~ i : l : :
I.J.ik~.,4s?>~~J + l9d~J~&-.J
l
· · · · · · · · · · --~
. . . 0. ~j.:1.
:.···---R
. .·_-_ ~
,;Sl
........ ··_<>
___ ~.·_• ·'·.·:·
. • , _.
•
--·i ...... ;.. ..;..... -t
1
L~
!i . . . .:.[ ;·'
:
.... :i
i
1
......
1
'
:
...... , ...... j ...... l ..... .(
Seite 2 von 6
D
P
Berufs-/Fachmittelschulen
Olten 1 Solothurn
Fach: Mathematik Geometrie
Aufnahmeprüfung 2012
Prüfungs-Nr. _ __
Zeit: 60 Min.
Aufgabe 2
Gegeben ist das Rechteck ABCD. Gesucht ist die Menge aller Punkte P innerhalb des
Rechtecks, die gleichzeitig
• naher bei der Seite AB ais bei der Seite AD liege11,
• naher bei der Ecke A ais bei der Ecke C liegen,
• und von D hôchstens den Abstand d = 8,0 cm haben.
Beachten Sie:
• Alle benéitigten Linien und Hilfslinien sind sichtbar zu konstruieren!
• Schraffieren Sie die Léisungsflache und ziehen Sie zusatzlich die zur Léisung
gehôrenden Randlinien farbig nach.
1. Winkelhalbierende
2. Mittelsenkrechte
3. Kreislinie
Bewertung:
Für die Konstruktion der drei Bedingungen total
2 Punkte. Bei jedem Fehler- 1 Punkt
Für die Uisungsflache Yz P
Für die Lôsungslinien Yz P
D
Aufnahmeprüfung BM/FMS 2012 Geometrie
Seite 3 von 6
Aufnahmeprüfung 2012
Berufs~/Fachmittelschulen
Olten 1 Solothurn
Fach: Mathematik Geometrie
Prüfungs~Nr.
_ __
Zeit: 60 Min.
Aufgabe 3
Eine 6,5 m lange Leiter wird von einer horizontalen Ebene aus an eine senl<rechte Wand
.
gestellt.
a)
b)
c)
d)
Das obere Ende erreicht an der Wand eine Ho he von 6,3 m. Wie weit ist das untere
Ende von der Hauswand entfernt?
Welcher Steigung in% entspricht die Situation von a)?
(Falls Sie Aufgabe a) nicht losen konnten, verwenden Sie ais Entfernung 2,24 m)
Die Lei ter wird so verschoben, dass die Steigung 240% betragt. Auf welcher Hiihe
berührt sie die Wand?
Der Steigungswinkel misst nun 60°. Auf welcher Hiihe wird die Wand jetzt berührt?
Ap
2.
D
AufnahmeprUfung BM/FMS 2012 Geometrie
Seite 4 von 6
Berufs-/Fachmittelschulen
Olten 1 Solothurn
Fach: IVIathematil< Geometrie
Aufnahmeprüfung 2012
Prüfungs-Nr. _ __
Zeit: 60 Min.
Aufgabe 4
Beim untenstehenden Konstruktionsplan sind folgende Masse bekannt:
AD = 18 dm, DE = 5 dm, EB = 4 dm und CD = 8,1 dm.
Berechnen Sie:
a) die Lange der Strecke EF.
b) die Lange der Strecke FI.
(Falls Sie Aufgabe a) nicht liisen l<onnten, rechnen Sie mit der Strecke EF = 3,9 dm)
c) die Lange der Strecke GH.
H
··-··-t·······(·---·j
i
i
:
··---~
i
;
;
;
·····1 ......,.. i
1
:
·---~
i
.
··· .. +·······j
i l
: ····--;-·· ··-r ·····r
·····T-i
:----\
····-r-···
l ..... j.
'--······t····
·i ·····; ·····• ··---~--
: ----l
j
!âp L.:J=,:I:tti:i ~ ? E.çj'J : 1 T ' j ' ! T ' i
f t j ......•........;......., ~4.···~-·-~··••l ::~tJ
:.:_· . . . .
i-
,
.,
.............,
·····r---- --i
j
----~---- ! ···--·~
, .•
. . . . . . . . . . . . . ;.-
r..
---i ------1--- ---! ······}
.
...
.
----+-·
-----i -----.l.-~--:~1------f----- -~-+ -----1 ....4;.
. ··r
.
-
...1 ······( ...... i........ ... ) ......·...... j ......; ······1 ...) ......: ······i·······+
l
j
l l
l
t
f
+
''
·····t ······~ ·····j ······j····
r
i)i
[ti
•·l
······:
.....j..)-='f
~/
JJ
....., ..... , .. _, · -•••••·.:_,_ :
i
+ :
i
:i-· ···j·. ·····-;--
f·--
;
······Î··· ...........; ..... -~- ·····.: ······+·
1
1
;
!
:!.. ...... !:
;
·····-;-··
··+
1
······!
······j·····
L_
j
:.~i ~r.:r~'+
:
:_. :
,
i
1
,
t··· ···i
'
c
l
:
rJ
•••••
i
'
i : ]
j
;
:
!
······! ····-+
·····~
j ...... j
l
:,:·····t.'.
i ' [ ,
1
:
---··f
:
1.
-----~
~
.... )
d
2
p
!1. 1kJ
2
-
/1
Je)
i
. J ; , , :. . )
·····-}
i
:
i
···~
!
i
!
j2 r
:_•--.::;),iÏj~bzhil i ! i J )1P
......!
······i
.....
··1
l. . ~ . . .
j
!
······j····
:
··!
'
······i ······i_-·-· ..................; ·····~
:
!
i
1 ~
;·······j ·····-; ······: ...... f ······t ·····~
······!
····+··· +··
: ......; ......!. ........; ..... ~
i
'
.
,l~·
~li
·
.
:
.
:
,
i
g
,
:
.
~
:
v
.
t
.
)
(
,
·
.
~
.
t
:z;~_ !·-~rt
·.:.-•·-•• .:..... )
1··-----'·.·.
····-ï ......;i · · ·-:,_: -····t! ......1i
· ·~1.- .....L .... L...... j ······!····-·
~
i
T
r. J
T-
·····1 ----i
..... .!
··+·······1········1·-·····1·······~
·····i ······j
i
: ......:
---~J-r\-~-~-çç/.?.1-----~
······i ------f ------i~, ,
l
~~/lïf,~j f 1
J ! + I l l ! :····i,
······:,1···· -·+ ·····Î·!
i
!
i
'
'
i
·····1····- ·:,: .............; ......f ......•......
i
j
j
j ....!.
LZ:tiL )(III~I?F~~ZLJ_: ~r:.:L!~_:?ri.: : t r
., ' '
i
·.1
......1...... j
-_-_-_-_-.1,_-··--
·····-~.......j
1
l ••••••(• --··1
······i
:
······t
...ij ......;i ......,..
:
T
!
: :
:.---- :
""""\ ······jl .... )
i ' : '
Il i l
·
,
f _-_-_.._-__·•:,_
··----1·-····i
i : ······t
·····t ....T .. ··i ......; ·····+···- ·! ······i ····+----) ··---~---··· ...... f ··-·--\- ····+ ......; ..... L._ ·1 ······i ······i ··-··-! ------} ·····~
i
AufnahmeprOfung BM/FMS 2012 Geometrie
j
l
Seite 5 von 6
D
Berufs-/Fachmittelschulen
Olten 1 Solothurn
Fach: Mathematik Geometrie
Aufnahmeprüfung 2012
Prüfungs-Nr. _ __
Zeit: 60 Min.
Aufgabe 5
Die Tunnelbohrmaschine Gabi vom Gotthardeisenbahnbasistunnel frast einen Zylinder aus
dem Berg. Der l<reisformige Querschnitt hat dabei einen Durchmesser von 9,58 m.
Der Tagesrekord an Tunnelvortrieb betragt 56 m.
a)
Wie vielen m3 Fels entspricht dieses Ausbruchsvolumen?
Vom Ausbruchsmaterial kann 64 % nicht mehr weiterve!Wertet werden. Dieses Abfallmaterial
wird deponiert und dabei zu einem Damm aufgeschüttet. Der Querschnitt dieses Dammes ist
ein gleichschenkliges Trapez ABCD gemass Skizze.
AB =16m, CD =10m, AD =5m
H
F
b)
Berechnen Sie die Ho he dieses Trapezes.
c)
Wie viele Meler betragt der Langenzuwachs BF des Dammes an diesem Rekordtag?
(Falls Sie Aufgabe a) und/oder b) nicht losen konnten, rechnen Sie mit einem totalen
Ausbruchsvolumen von 3'500 m3 und einer Dammhühe von 4,5m).
dp
2
D
Aufnahmeprüfung BM/FMS 2012 Geometrie
Seite 6 von 6
Berufs-/Fachmittelschulen
Olten 1 $olothurn
Fach: Mathematik Geometrie
Aufnahmeprüfung 2012
Uisungen
Zeit: 60 Min.
Aufgabe 1
(1 Yz P)
a) y= 74°
b) ~
= goo+a
2
(1 Yz P)
Aufgabe 2
1. Winkelhalbierende
2. Mittelsenkrechte
3. Kreislinie
Bewertung:
FUr die Konstruktion der drei Bedingungen total
2 Punkte. Bei jedem Fehler- 1 Punkt
FUr die Liisungsflache Yz P
FUr die Uisungslinien Yz P
Aufgabe 3
a)
b)
c)
d)
1,6 m
393,75% (281,25 %)
6m
5,63 m
(% P)
(% P)
(1 P)
(1 P)
Aufgabe 4
a) EF = 3,6 dm
b) FI= 15 dm (14 dm)
c) GH = 2,25 dm
(1 P)
(1 P)
(1 P)
Aufgabe 5
a) 4'036,537 m 3
b) 4 m
c) 49,68 m (38,29 m)
(1 P)
(% P)
(1% P)
AufnahmeprUfung BM/FMS 2012 Geometrie
Sei!e 1 von 1