GEOMETRIE (4a) - Universität Koblenz · Landau

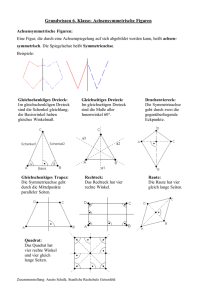
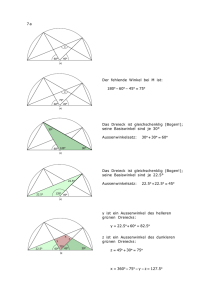
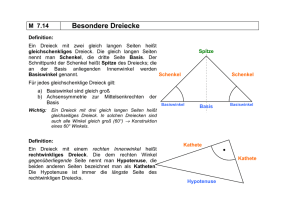
CAMPUS LANDAU
INSTITUT FÜR MATHEMATIK
Maximilian Geier
GEOMETRIE (4a)
Wintersemester 2015/16
Übungsblatt 10
Aufgaben zur Vorlesung vom 21.01.2016
Abgabe bis Mittwoch, 27.01.2016
Wir beweisen in den Aufgaben 1-2 schon jetzt die Aussagen von Satz 2.27. Dazu sei zunächst daran
erinnert: Nebenwinkel ergänzen sich zu einem gestreckten Winkel. In Aufgabe 2 kann durch
Betrachtung geeigneter zusätzlicher Geraden ein Kongruenzsatz angewendet werden.
Aufgabe 1
(1P)
Zeigen Sie:
Scheitelwinkel sind kongruent
Aufgabe 2
(2P)
Zeigen Sie:
Stufenwinkel und Wechselwinkel an parallelen Geraden sind kongruent
Ein klassischer Beweis der folgenden Behauptung nutzt die Aussage aus Aufgabe 2:
Aufgabe 3
(1P)
Zeigen Sie:
Die Innenwinkel eines Dreiecks ergänzen sich zu einem gestreckten Winkel
Aufgabe 4
(3P)
Definitionen:
Ein Viereck mit zwei Paaren kongruenter benachbarter Seiten heißt
Drachenviereck. Ein Viereck, bei dem alle Seiten kongruent sind, heißt Raute.
Ein Dreieck mit zwei zueinander kongruenten Seiten heißt gleichschenkliges
Dreieck. Die beiden kongruenten Seiten heißen dann Schenkel, die dritte Seite
Basis des Dreiecks. Die beiden an der Basis liegenden Winkel heißen dann
Basiswinkel.
Beweisen Sie folgenden Aussagen mit Hilfe von Kongruenzsätzen


Aufgabe 5
(2P)
Ein Drachenviereck, in dem sich die Diagonalen gegenseitig halbieren,
ist eine Raute.
Jedes gleichschenklige Dreieck ist achsensymmetrisch, und seine
Basiswinkel sind kongruent.
Zeigen Sie:
Die Addition auf der Menge aller positiv orientierten Winkelgrößen ist
assoziativ.
Die Addition auf der Menge aller orientierten Winkelgrößen ist nicht
assoziativ.