Aufgaben - Mathe für jung und alt

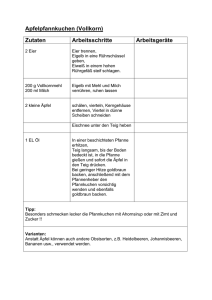
MATHE FÜR JUNG UND ALT - SERIE95 - MÄRZ/APRIL 2014
1
1
Vorschule
Aufgabe 95-11
Hier siehst Du einen Nähkasten unten und einen Werkzeugkasten oben. Male die Gegenstände, die in den Werkzeugtkasten gehören, farbig aus und wenn Du möchtest, die
Gegenstände, die in den Nähkasten gehören, mit einer anderen Farbe.
Aufgabe 95-12
Pia und ihre Mutter arbeiten im Garten. Pias Mutter pflanzt 4 Himbeersträucher in eine
Reihe am Zaun entlang. Zwischen die Himbeersträucher pflanzt Pias Mutter immer zwei
Brombeersträucher. Pia pflanzt in jede Lücke zwischen zwei Sträuchern eine Rose.
Wie viele Rosen pflanzt Pia?
2
Heike Winkelvoß, www.egladil.de
Aufgabe 95-13
Wie viele Dreiecke kann man in dieser Figur finden?
Aufgabe 95-14
Leo Köhnlein, 8 Jahre, Klasse 2
Simon, Anna und Ben haben zusammen 30 Murmeln. Ben verliert 5 Murmeln, findet
aber wieder 3. Anna bekommt 4 Murmeln geschenkt und verliert 1 Murmel wieder. Simon
verliert 13 Murmeln.
Wie viele Murmeln haben alle jetzt zusammen?
Aufgabe 95-15
In jeder Zeile steht genau ein Wort, ein Buchstabe oder eine Zahl, welche nicht dazu
gehören. Finde heraus, was es ist und begründe deine Wahl.
a) Kirsche, Pflaume, Pfirsich, Erdbeere, Nektarine, Mirabelle
b) A, 9, C, X, P, M
c) Springseil, Ball, Roller, Bausteine, Fahrrad
d) Bürste, Seife, Zahnpasta, Teller, Waschlappen
e) 24, 3, 7, 2, 5
f) ANNA, OTTO, KARL, HANNAH, ADA
Erfinde 2 weitere solcher Rätsel, gib die Lösung an und begründe.
MATHE FÜR JUNG UND ALT - SERIE95 - MÄRZ/APRIL 2014
3
Aufgabe 95-16
Hier siehst du 4 Bilder und ihre Spiegelbilder. Aber es haben sich Fehler eingeschlichen.
Welche Spiegelbilder sind falsch?
2
Klassen 1 und 2
Aufgabe 95-21
Riccardo Mann, 6 Jahre, Klasse 1:
Wenn ein Junge in einer Minute 80 mal übers Seil springt, wieviel Mal springt er dann in
8 Minuten?
Aufgabe 95-22
Ein listiger Spion hat sich eine Geheimzahl zum Verschlüsseln ausgedacht. Damit niemand
diese errät, rechnet er damit nacheinander:
+5
:3
·4
−6
:7
Als Ergebnis erhält er die Zahl 2.
Welche Geheimzahl hat sich der Spion ausgedacht?
4
Heike Winkelvoß, www.egladil.de
Aufgabe 95-23
Leo Köhnlein, 8 Jahre, Klasse 2
Male die jedes Kästchen in dieser Reihe aus.
2
6
7
10
1
9
5
8
0
17
Dabei gilt:
1. Die Zahl, die gleich weit von der grünen Zahl und der orangenen Zahl ist, ist lila.
2. grüne Zahl + rote Zahl = orange Zahl
3. orange Zahl − rote Zahl − gelbe Zahl − gelbe Zahl = graue Zahl
4. Die Zahl, die rechts neben der roten Zahl steht, ist grün.
5. Die Hälfte der gelben Zahl ist die blaue Zahl.
6. grüne Zahl − rote Zahl + lila Zahl + blaue Zahl = weiße Zahl
7. Die Zahl, die links neben der orangen Zahl steht, ist olivgrün.
8. 4 · gelbe Zahl = rosa Zahl
9. Die 7 ist rot.
10. rote Zahl - lila Zahl = gelbe Zahl
Aufgabe 95-24
Ein Junge ersetzte der Reihe nach jeden Buchstaben seines Vornamens durch die Nummer
dieses Buchstaben im Alphabet. Er erhielt die Zahl
51213118
Wie heißt der Junge?
Aufgabe 95-25
Schau genau: unter diesen Bruchstücken gibt es genau zwei, die zusammen eine vollständige Eierschale ergeben. Welche sind es?
MATHE FÜR JUNG UND ALT - SERIE95 - MÄRZ/APRIL 2014
5
Aufgabe 95-26
Julia hat für ihre Freunde ein Zahlenrätsel erfunden. In dem Wort OSTERN hat sie
jeden Buchstaben durch eine Zahl ersetzt und dies aufgeschrieben:
S+T +E
T ·E
E+R
N
E
O+S+T +E+R+N
=
=
=
=
=
=
16
18
81 : 9
4·E
8:4
34
Löse Julias Zahlenrätsel.
Aufgabe 95-27
Setze die Zahlen 6, 12, 15 und 21 so in die Kästchen und Rechenzeichen + und − in die
Kreise ein, dass die Gleichung stimmt.
=
0
Aufgabe 95-28
Der Postbote muss 9 Briefe zustellen. Er will das tun, ohne einen Weg zweimal zu fahren.
Wie muss er fahren?
6
3
Heike Winkelvoß, www.egladil.de
Klassen 3 und 4
Aufgabe 95-31
Maike Kadelka, 9 Jahre, Klasse 4:
Ich habe 5 Würfel gebaut. 4 Würfel sind ganz fertig, das heißt mit allen Augen versehen.
Bei einem Würfel fehlen noch 9 Augen. Beantworte folgende Fragen und begründe deine
Antworten:
a) Welche Augen könnten schon auf dem fünften Würfel stehen?
b) Welche Augen könnten noch fehlen?
c) Wie viele Würfelaugen sind insgesamt schon vergeben ?
Aufgabe 95-32
Wer knackt den Code?
In diesem Kryptogramm bedeutet jeder Buchstabe eine Ziffer. Gleiche Buchstaben bedeuten gleiche Ziffern, verschiedene Buchstaben verschiedene Ziffern.
AB + C = AC
·
+
+
D · E = AC
DB − F = CE
Aufgabe 95-33
Lisa Schöttl, 8 Jahre, Klasse 3:
Maria malt ein Bild an und benutzt dabei Wasserfarben. Das Bild ist 11 cm lang und 8
cm breit. Für jeden cm2 braucht Maria 20 Tropfen Farbe.
Wieviel Tropfen braucht sie für das ganze Bild?
Aufgabe 95-34
Es ist Nacht. Ein Junge, sein Vater, seine Mutter und seine Großmutter stehen am Ufer
eines Flusses und wollen über eine unbeleuchtete Brücke ans andere Ufer gelangen. Sie
haben nur eine Taschenlampe dabei. Über die Brücke können höchstens zwei Personen
gehen und müssen dabei die Taschenlampe mit sich führen. Der Vater kann die Brücke
in einer Minute überqueren, der Junge in 2 Minuten, die Mutter in 5 Minuten und die
Großmutter in 10 Minuten.
Welche Zeit brauchen sie mindestens, um den Fluss zu überqueren?
MATHE FÜR JUNG UND ALT - SERIE95 - MÄRZ/APRIL 2014
7
Aufgabe 95-35
Aufgabe von Jonas Werth, 9 Jahre, Klasse 4:
Gesucht sind 4 Zahlen, für die Folgendes gilt:
(1) Alle Zahlen sind ungerade und liegen zwischen 30 und 90.
(2) Ihre Summe ist gleich 248.
(3) Alle Zahlen sind voneinander verschieden.
(4) Alle Zehner sind voneinander verschieden.
(5) Alle Einer sind voneinander verschieden.
Aufgabe 95-36
Gehe von irgendeinem Punkt aus so
durch das Labyrinth, dass alle sieben
Punkte berührt werden! Schwarze Linien darfst du dabei nicht kreuzen. Wie
musst du starten, wo ist das Ziel?
Aufgabe 95-37
Ich denke mir eine Zahl. Wenn ich von der gedachten Zahl erst 7 subtrahiere und dann
das Ergebnis mit 7 multipliziere oder von der gedachten Zahl erst 3 subtrahiere und dann
das Ergebnis mit 3 multipliziere, erhalte ich jedes Mal das gleiche Resultat.
Welche Zahl habe ich mir gedacht? Gibt es mehr als eine Zahl, die ich mir gedacht haben
könnte? Wenn ja, gib eine weitere Zahl an, wenn nicht, begründe.
Aufgabe 95-38
Von 11 Kindern der Theater-AG sind genau 3 Kinder auch in der Mathe-AG. In der
Sport-AG sind insgesamt 12 Kinder. In der Mathe-AG sind insgesamt 13 Kinder. Genau
ein Kind aus der Sport-AG ist auch in der Theater-AG und genau ein anderes Kind aus
der Sport-AG ist auch in der Mathe-AG. In allen 3 AGs zugleich ist kein Kind.
Theater
a) Wie viele Kinder insgesamt sind in den 3 AGs?
b) Wie viele Kinder sind nur in einer AG?
Tipp: vielleicht hilft dir eine Zeichnung weiter:
Mathe
Sport
8
4
Heike Winkelvoß, www.egladil.de
Klassen 5 und 6
Aufgabe 95-41
Eine Mutter hat drei Kinder. Die jüngste Tochter ist (in ganzen Jahren) so alt, wie die
erste Stelle des Alters der Mutter (in ganzen Jahren), die ältere Tochter so alt wie die
zweite Stelle des Alters der Mutter. Das Alter des Sohnes ist gleich der Quersumme des
Alters der Mutter. Zusammen sind alle vier 33 Jahre alt.
Wie alt ist die Mutter?
Aufgabe 95-42
Jonas ergänzt einen Summanden einer Summe von zwei natürlichen Zahlen um eine zusätzliche Null am Ende und erhält statt 2807 die Summe 10007. Wie lauten die beiden
Summanden?
Aufgabe 95-43
An einem kreisrunden Tisch sitzen 15 Kinder. Rechts von jedem Mädchen sitzt ein Junge.
Die Hälfte der Jungen hat als rechten Nachbarn ebenfalls einen Jungen, die andere Hälfte
hat ein Mädchen als rechte Nachbarin.
Wie viele Jungen und wie viele Mädchen sitzen am Tisch?
Aufgabe 95-44
In einer Kiste liegen grüne, gelbe und rote Äpfel in 3 Sorten. Ist es möglich, dass es mehr
grüne Äpfel sind, als Äpfel der ersten Sorte, mehr Äpfel der ersten Sorte als gelbe Äpfel,
mehr gelbe Äpfel als Äpfel der zweiten Sorte, mehr Äpfel der zweiten Sorte als rote Äpfel
und mehr rote Äpfel als Äpfel der dritten Sorte?
Aufgabe 95-45
Gegeben ist ein Rechteck mit den Seitenlängen 3 cm und 4 cm. Teile dieses Rechteck durch
zwei gerade Schnitte in drei flächengleiche Stücke. Du darfst nur Zirkel und Lineal zur
Konstruktion der Schnittlinien verwenden. Gib mindestens zwei verschiedene Lösungen
an.
Hinweis: flächengleich heißt nicht notwendig kongruent.
MATHE FÜR JUNG UND ALT - SERIE95 - MÄRZ/APRIL 2014
9
Aufgabe 95-46
U. Warnecke, Münster:
Es ist z. B.: 2 + 2 = 2 · 2; 3 + 23 = 3 · 32 ; (−1) + 12 = (−1) · 12 .
So gibt es zu jeder Zahl a – bis auf eine Ausnahme – eine Zahl b, so dass gilt a + b = a · b.
Welche Zahl bildet hier die Ausnahme und warum? Beweise auch, dass es nur diese eine
Ausnahme gibt.
Aufgabe 95-47
U. Warnecke, Münster:
Zwei Züge mit den Geschwindigkeiten v1 = 45km/h und v2 = 36 km/h begegnen einander.
Ein Fahrgast stellt fest: die Begegnung hat 6 Sekunden gedauert.
Wie lang ist der Zug, in dem sich der Fahrgast befindet?
Aufgabe 95-48
C
Im Dreieck ABC seien M der Mittelpunkt der Seite AB
und P ein beliebiger innerer Punkt der Strecke CM.
Beweise, dass die beiden grau markierten Dreiecke, AP C
und BP C, dann den gleichen Flächeninhalt haben.
P
A
5
M
B
Klassen 7 und 8
Aufgabe 95-51
Aus 27 Einheitswürfeln sei ein 3 × 3 × 3 Würfel zusammengesetzt. Über diesen großen
Würfel soll eine Ameise von kleinem Würfel zu kleinem Würfel wandern. Dabei darf sie
sich von jedem kleinen Würfel auf einen benachbarten bewegen (einen, der mit diesem
eine gemeinsame Seite besitzt), aber es ist ihr nicht erlaubt, zweimal hintereinander in
die gleiche Richtung zu laufen.
Kann die Ameise auf diese Weise jeden der 26 äußeren kleinen Würfel genau einmal
besuchen?
10
Heike Winkelvoß, www.egladil.de
Aufgabe 95-52
Das arithmetische Mittel zweier reeller Zahlen x, y ist definiert als
x+y
2
das harmonische Mittel als
1
x
2
+
1
y
An einer Tafel im Mathekabinett stehen die beiden Zahlen 1 und 2. Jeden Tag wischt der
Mathelehrer die beiden Zahlen ab und ersetzt die erste durch deren aritmetisches Mittel,
die zweite durch ihr harmonisches Mittel.
Wie lautet das Produkt der beiden Zahlen, die er nach 2006 Tagen an die Tafel schreiben
wird?
Zusatzaufgabe: Kann er es schaffen, am 2006. Tag die beiden neuen Zahlen aufzuschreiben?
Aufgabe 95-53
In einer Schule gibt es 1000 Schülerspinde mit den Nummern 1, 2, . . . , 1000. Jeder Spind
ist nachts immer zugeschlossen. In der Schule leben außerdem 1000 Gespenster. Genau
um Mitternacht schließt das erste Gespenst alle Spinde auf. Anschließend schließt das
zweite Gespenst alle Spinde mit geraden Nummern wieder zu. Dann vertauscht das dritte
Gespenst den Zustand der Spinde, deren Nummern durch 3 teilbar sind: ist der Spind geöffnet, schließt er ihn ab, ist er verschlossen, öffnet er ihn. Das vierte Gespenst verstauscht
den Zustand aller Spinde mit durch 4 teilbaren Nummern usw. Am Ende vertauscht das
1000. Gespenst den Zustand des Spinds Nummer 1000. Dann verschwinden die Gespenster
wieder.
Wie viele Spinde sind am nächsten Morgen geöffnet?
Aufgabe 95-54
Yak lebt auf einem fremden Planeten und lernt gerade, wie man die zwei Einheiten Kulo und Pfend für die Masse ineinander umrechnet: Um eine Masse von Pfend in Kulo
umzurechnen, muss Yak die Maßzahl durch 2 teilen und das Ergebnis um 20 % verringern (zufällig funktionieren die Rechenoperationen und die Prozentrechnung auf diesem
Planeten genauso wie bei uns). „Aha!“ , denkt sich Yak. „Wenn ich von Kulo in Pfend
zurückrechnen will, muss ich nur die Maßzahl verdoppeln und anschließend das Ergebnis
um 20 % erhöhen.“ Du hast natürlich gleich gemerkt, dass das nicht stimmen kann. Um
wieviel Prozent wird sich Yak auf diese Weise verrechnen?
MATHE FÜR JUNG UND ALT - SERIE95 - MÄRZ/APRIL 2014
11
Aufgabe 95-55
Finde eine natürliche Zahl a für die von folgenden Aussagen zwei wahr sind und eine
falsch ist
1. a + 51 ist eine Quadratzahl.
2. a endet auf 1.
3. a − 38 ist eine Quadratzahl.
Aufgabe 95-56
Es seien ABCD ein Quadrat und E der Mittelpunkt der Seite
DA. Ferner sei M der Mittelpung der Strecke EC (vgl. das
Bild). Man entscheide, ob der Flächeninhalt des in der Abbildung weiß gefärbten Vierecks ABME größer, kleiner oder
gleich dem Flächeninhalt des in der Abbildung grau gefärbten
Fünfecks EMBCD ist. Erst schätzen, dann die Flächeninhalte berechnen.
D
C
M
E
A
B
Aufgabe 95-57
Es seien a und c mit a < c zwei positive reelle Zahlen. Man gebe alle positiven reellen
Zahlen x an, für die die Gleichung
a+x
=c
1 + ax
2
c
gilt.
Aufgabe 95-58
U. Warnecke, Münster:
Für eine natürliche Zahl n bezeichnet n! (sprich: n Fakultät) das Produkt aller natürlichen
Zahlen von 1 bis n, also z. B. 5! = 1 · 2 · 3 · 4 · 5. (Für n = 1 ist 1! = 1.)
Bestimme alle natürlichen Zahlen, für die die Summe 1!+2!+3!+. . .+n! eine Quadratzahl
wird.
12
6
Heike Winkelvoß, www.egladil.de
Klassen 9 bis 13
Aufgabe 95-61
Es seien a1 , a2 , a3 , . . . a2007 beliebige ganze Zahlen, b1 , b2 , b3 , . . . b2007 eine Permutation (Vertauschung) dieser Zahlen. Beweise, dass das Produkt (a1 − b1 )(a2 − b2 ) · · · (a2007 − b2007 )
gerade ist.
Aufgabe 95-62
Beweise, dass der Nachfolger des Produkts von 4 aufeinanderfolgenden natürlichen Zahlen
stets eine Quadratzahl ist.
Aufgabe 95-63
Man beweise, dass es keine rationalen Zahlen x, y gibt für die
x2 + y 2 = 7
gilt.
Aufgabe 95-64
U. Warnecke, Münster:
Zeige, dass für alle natürlichen Zahlen (einschließlich 0) folgende Ungleichung gilt:
(n − 1)2 (n2 − 1)n−1 < n2n .
Aufgabe 95-65
Einem Halbkreis mit dem Durchmesser AB seien zwei Halbkreise einbeschrieben, deren Durchmesser AC und
BC auf AB liegen und einander im
Punkt C berühren. Die Senkrechte zu
AB durch C schneide den Halbkreis
über AB im Punkt D. Ist der Flächeninhalt des Kreises mit Durchmesser CD
(grau gezeichnet) kleiner, gleich oder
größer dem Flächeninhalt der Fläche,
die durch die 3 Halbkreisbögen über
AB, AC und BC begrenzt wird (grün
gezeichnet)?
MATHE FÜR JUNG UND ALT - SERIE95 - MÄRZ/APRIL 2014
13
Aufgabe 95-66
Zwei kongruente Rechtecke liegen so, dass ihre Ränder
einander in 8 Punkten schneiden. Man beweise, dass
der Flächeninhalt der von beiden Rechtecken gleichzeitig
überdeckten Fläche (also der Durchschnitt der Rechtecke als Puntmengen) größer als die Hälfte des Flächeninhalts jedes der beiden Rechtecke ist.
Quellennachweis:
Aufgabe 95-11: Leipziger Volkszeitung(1)1983
Aufgabe 95-15: Leo Köhnlein, 8 Jahre, Klasse 2
Aufgabe 95-21: Riccardo Mann, 6 Jahre, Klasse 1
Aufgabe 95-23: Leo Köhnlein, 8 Jahre, Klasse 2
Aufgabe 95-25: alpha(2)1984
Aufgabe 95-28: alpha(1)1980
Aufgabe 95-31: Maike Kadelka, 9 Jahre, Klasse 4
Aufgabe 95-32: Lu.a.Ma. (Mathewettbewerb des Leibniz-Gymnasiums Wiesbaden)(11)2005
Aufgabe 95-33: Lisa Schoettl, 8 Jahre, Klasse 3
Aufgabe 95-34: M.A.Jewdokimow: Von Aufgabe zu Aufgabe, S.7
Aufgabe 95-35: Jonas Werth, 9 Jahre, Klasse 4
Aufgabe 95-36: Leipziger Volkszeitung(1)1983
Aufgabe 95-43: Moskauer Mathematikolympiade(2055)2001
Aufgabe 95-44: kvant(4)2000
Aufgabe 95-46: Ulrich Warnecke, Münster
Aufgabe 95-47: Ulrich Warnecke, Münster
Aufgabe 95-53: M.A.Jewdokimow: Von Aufgabe zu Aufgabe, S.9
Aufgabe 95-55: I.L.Babinskaja: Aufgaben mathematischer Olympiaden, S.93
Aufgabe 95-56: alpha(5)1975
Aufgabe 95-57: alpha(5)1975
Aufgabe 95-58: Ulrich Warnecke, Münster
Aufgabe 95-63: alpha(5)1975
Aufgabe 95-64: Ulrich Warnecke, Münster
Aufgabe 95-65: kvant(5)1971
Aufgabe 95-66: kvant(11)1970
Rest: Heike Winkelvoß