Trigonometrie, 1. Teil TR1
Werbung

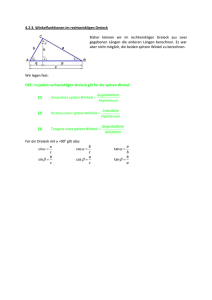
Trigonometrie, 1. Teil Mathematik TR1 T. Hunziker, dipl. math., dipl. ML www.hunziker.jimdo.com Okt 14 Hilfsmittel: Formelsammlung GBMS, Taschenrechner Schlussresultate wenn nötig auf 2 Dezimalen runden Einführung Das Wort Trigonometrie bedeutet „Dreiwinkelmessung“, oder allgemein „Dreiecksberechnung“. Wenn von einem Dreieck drei Stücke (z.B. Seiten oder Winkel) gegeben sind, dann können wir das Dreieck konstruieren. Dagegen ist es uns bislang nicht möglich, die fehlenden Stücke zu berechnen. Diese Aufgabe übernimmt die Trigonometrie. Der Einfachheit halber beschränken wir uns zunächst auf rechtwinklige Dreiecke. Die Trigonometrie als Bindeglied zwischen Winkeln und Strecken Zieht man in einem rechtwinkligen Dreieck ABC zur Kathete a Parallelen a1 ,a2 usw., so entstehen rechtwinklige Dreiecke AB1 C 1 , A B2 C 2 . Diese Dreiecke haben allesamt gleiche Gestalt, das heisst sie sind einander ähnlich. Die Seitenverhältnisse in diesen Dreiecken sind gleich. So gilt etwa: a a a = 1 = 2. c c1 c2 Dieses Seitenverhältnis ist durch den Winkel eindeutig bestimmt. Man kann ein solches Seitenverhältnis deshalb als eine Funktion des Winkels betrachten, und zwar als trigonometrische Funktion von . Durch die Trigonometrie kann man also Winkel mit Streckenverhältnissen identifizieren und umgekehrt. Auf diese Weise kommt man über die metrische Geometrie der Ebene, die hauptsächlich nur Beziehungen zwischen Strecken kennt, hinaus. Man denke an die Satzgruppe des Pythagoras, die nur Aussagen über Beziehungen zwischen Strecken macht. Sinus, Kosinus und Tangens In einem rechtwinkligen Dreieck heisst die einem spitzen Winkel gegenüberliegende Kathete seine Gegenkathete (Gk), die andere seine Ankathete (Ak). a Gegenkathete (Gk) von a Ankathete (Ak) von a sin α = : Gk von α Hyp ● Sinus des Winkels ● Cosinus des Winkels : cosα = Ak von α Hyp ● Tangens des Winkels : tan α = Gk von α Ak von α Gk = Gegenkathete [lies:'Sinus Alpha' oder 'Sinus von Alpha'] (Steigung) Ak = Ankathete Hyp = Hypotenuse Aufgabe 1 Gegeben ist ein rechtwinkliges Dreieck mit der Kathete a = 3 cm und der Hypotenuse c = 6 cm. (siehe Abbildung rechts). C a) Berechnen Sie mit dem Satz von Pythagoras die Seite b (auf 2 Dezimalen runden). b b = .................. cm A b) Messen Sie mit dem Geodreieck die Winkel: =.............. = a = 3 cm B c = 6 cm =.............. ...................... c) Welches ist die Ankathete von Welches ist die Ankathete von ? ? Welches ist die Gegenkathete von Welches ist die Gegenkathete von ? ? d) Berechnen Sie nun den Sinus, Cosinus und Tangens des Winkels auf zwei verschiedene Arten: einerseits, indem Sie die Seitenverhältnisse ausrechnen, und andererseits, indem Sie auf dem Taschenrechner direkt die Winkelfunktionen abrufen. Füllen Sie die Tabelle aus: sin Berechnung per Seitenverhältnis sin α = cos tan G = H Berechnung per Taschenrechner Aufgabe 2 Ergänzen Sie die Tabelle: Dreieck Winkel ABC ADC BCD 1 Gegenkathete p Ankathete h Hypotenuse b sin cos tan 2 C 1 2 b p b h b p h a h A p q c D B Aufgabe 3 Wie hoch ist eine Tanne, wenn ihr Schatten s = 27.5 m lang ist und die Sonnenstrahlen unter dem Winkel = 38.5° einfallen? Berechnen Sie mit dem Taschenrechner. Aufgabe 4 Das Dreieck ABC ist gleichschenklig. Berechnen Sie alle fehlenden Seiten und Winkel, sowie den Flächeninhalt des Dreiecks. C a=45.2m; =98° b a h A Aufgabe 5 Ein Rhombus hat eine Seitenlänge von s = 9.4 cm. Einer der vier Innenwinkel misst 58°. Berechnen Sie den Flächeninhalt des Rhombus. c B Aufgabe 6 Welche Steigung in Prozent hat eine Strasse mit einem Steigungswinkel von a) 5° b) 20° d) 70° e) a° c) 45° Aufgabe 7 a) Zeichnen Sie rechts ein regelmässiges Fünfeck mit einem Umkreisradius von 3 cm. b) Berechnen Sie die Seitenlänge s und den Flächeninhalt A des Fünfecks! Aufgabe 8 Gegeben: Ein Rechteck mit der Diagonale d und dem Winkel α (siehe Abbildung) Gesucht: der Flächeninhalt A des Rechtecks. Gesucht ist eine möglichst einfache Formel für A, bei gegebenem d und α! d a