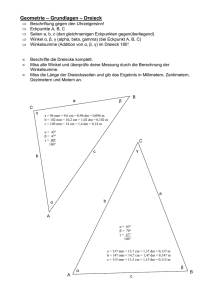
Aufgabenblatt 9

Prof. S. Krauter
1.
MODUL 2 – R – H. Geometrie SoSe 05.
Blatt 9 – Lösungen
a) α = 75°. Man betrachte das gleichseitige Dreieck mit Seitenlänge a in der
rechten Hälfte der Figur und das gleichschenklige Dreieck mit Schenkellänge a
in der unteren Hälfte der Figur.
b) α = 36°. Man betrachte hierzu das auf der Spitze stehende gleichschenklige
Dreieck in der Mitte. Es hat Basiswinkel mit dem Maß 2α (Warum?).
2. a) 1. BC = a; 2. Umkreismitte U liegt auf der Mittelsenkrechten von a und auf
k(B; ru).
3. A erhält man durch k und β.
b) D sei der Schnittpunkt von wα mit BC. Teildreieck CAD ist eindeutig bestimmt
(SWS). Restliche Konstruktion ist klar.
c) 1. α
2. Man erhält die Inkreismitte J durch die Winkelhalbierende von
α und die Parallele zu AB im Abstand ρ = ri. 3. Tangente an Inkreis, die mit
AB den Winkel β bildet (z. B. mit Hilfe der Winkelhalbierenden BJ).
d) Sei D Höhenfußpunkt von hc auf AB. Dann ist Teildreieck ADC eindeutig
bestimmt durch b, hc und den rechten Winkel (SsW). Rest ist klar.
e) 1. Umkreis k(U; ru).
2. Sehne BC = a in k.
3. Parallele zu BC im
Abstand ha ergibt A.
f) Teildreieck BSMc ist eindeutig bestimmt (SSS). Restkonstruktion ist klar.
g) Wegen γ = 90° ist AB Durchmesser des Umkreises k mit Radius 4 cm. Damit
ist die Konstruktion klar.
h) Man konstruiert zunächst ein zur Lösung ähnliches beliebiges Dreieck A’B’C’
mit α = 75° und γ = 60° und dessen Umkreismitte U samt Umkreis k’. Dann
zeichnet man um U den Kreis k=k(U; ru) und an diesen parallele Sehnen zu
den Seiten des Dreiecks A’B’C’ (maßstäbliches Vergrößern bzw. zentrische
Streckung aus U). Der Schnitt von UA’ mit k liefert z.B. A usw.
3. a) Die Punkte C liegen alle auf demselben Fasskreisbogen(-paar), also haben
alle diese Dreiecke denselben Umkreisradius bzw. -durchmesser.
b) Zunächst sei U die Umkreismitte und Mc die Mitte von AB.
Dann ist ∠AUMc = α und im rechtwinkligen Dreieck AUMc gilt: sin α = a/2 : r.
Analog gilt dies für die beiden anderen Seiten und die Behauptung ist
bewiesen.
Die ursprüngliche rein qualitative Aussage „zur größeren Seite gehört der
größere Gegenwinkel“ ist nicht proportional, es gilt also nicht a : b = α : β
(nennen Sie einfache Gegenbeispiele). Stattdessen gilt: Die Seiten verhalten
sich wie die Sinuswerte ihrer Gegenwinkel, d.h. a : b = sin α : sin β.
4.
Setzt man an ein Dreieck mit der Winkelsumme 180° ein weiteres an, so erhält
man ein Viereck mit der Winkelsumme der beiden Dreiecke. So fortfahrend
erhält man die Winkelsumme in n-Ecken:
Wn = 180° + (n – 3) * 180° = n * 180° – 360° = 180° * (n – 2)
Für ein Dreieck benötigt man 3 Bestimmungsstücke. Setzt man daran ein
weiteres Dreieck mit einer schon vorhandenen Seite an, so benötigt man nur
noch zwei weitere Stücke. So fortfahrend erhält man die Zahl der
Bestimmungsstücke für ein beliebiges n-Eck: Bn = 3 + (n – 3) * 2 = 2 * n – 3.
5.
Quadrat und regelmäßiges Sechseck sind leicht mit Zirkel und Lineal allein
konstruierbar. Durch Winkelhalbierung erhält man dann regelmäßige Vielecke
mit den doppelten Eckenzahlen.
Die Berechnungen liefern schöne Anwendungen für die Satzgruppe des
Pythagoras.
6. a)
Seien p und q die Seiten des Rechtecks. Dann konstruiert man entweder mit
dem Kathetensatz oder mit dem Höhensatz ein dazu inhaltsgleiches
Rechteck.
b) Man konstruiert mit Hilfe des Höhensatzes: Die Hypotenuse ist der halbe
Umfang des Rechtecks aus den Hypotenusenabschnitten.
Ein rechtwinkliges Dreieck mit u/2 als Hypotenuse und der gegebenen
Quadratseite als Höhe auf der Hypotenuse liefert die Lösung.
c) Man geht schrittweise vor:
Im ersten Schritt konstruiert man ein zum Dreieck inhaltsgleiches Rechteck
und zu diesem nach a) ein inhaltsgleiches Quadrat mit der Seite s.
Dann konstruiert man gemäß b) ein zu diesem Quadrat inhaltsgleiches
Rechteck mit vorgeschriebenem Umfang, nämlich genau dem des
gegebenen Dreiecks.
7.
Lösungen siehe im Skript.
8.
Zunächst ist die Oberfläche klar, denn sie besteht aus 8 gleichseitigen Dreiecken
und 18 Quadraten jeweils mit der Seite a:
a²
* 3 + 18 * a² = a² * (18 + 2 * 3 )
A=8*
4
Das Volumen erhält man durch geschicktes Zusammenstückeln:
Das horizontal liegende Band von 8 Quadraten bildet eine Säule mit Höhe a und
dem regelmäßigen Achteck mit der Seite A als Grundfläche. Sein Beitrag ist also
V1 = a * (a² + a² + 4 * a * a/ 2 ) = a³ * 2 * (1 + 2 )
Dann erhält man über dem Mittenquadrat je eine Säule nach oben und unten mit
Grundfläche a² und Höhe a/ 2 . Das liefert den Beitrag
V2 = 2 * a² * a/ 2 = a³ * 2 .
Die acht Dreieckssäulen mit gleichschenklig-rechtwinkligen Dreiecken der
Seitenlänge a/ 2 und jeweils der Höhe h jeweils im seitlichen Mittelteil unten
und oben ergeben den Anteil
V3 = 8 * ½ * a/ 2 * a/ 2 * a = 2 * a³.
Schließlich tragen die verbliebenen Eckpyramiden, die man zu einer
Doppelpyramide (regelmäßiges Oktaeder) mit Seitenkante a zusammenstellen
kann, noch bei:
V4 = 2 * 1/3 * a² * a/ 2 = a³ *
2
.
3
Die Summe V1 + V2 + V3 + V4 ergibt das Gesamtvolumen:
2
= a³ * (4 + 10/3 * 2 )
3
Andere Zerlegungen sollten zum selben Endergebnis führen.
Das kleine Rhombenkuboktaeder ist ein archimedischer Körper. Das PseudoRhombenkuboktaeder entsteht aus dem Rhombenkuboktaeder, indem man eine
Kappe des Körpers ablöst und nach Drehung um 45° wieder aufsetzt. Es gibt
dann nur noch ein Band aus acht Quadraten, das einmal um den Körper verläuft.
Es ist ein Körper, der einer lokalen Definition der archimedischen Körper
(nämlich der Uniformität der Ecken) genügt, nicht jedoch einer globalen (nämlich
der Tatsache, dass die Drehgruppe des Polyeders transitiv auf seinen Ecken
operiert). Es wurde erst im Jahre 1930 von Miller (daher auch der Name
Millerscher Körper) entdeckt; bis dahin war man der Meinung, dass die lokale
und die globale Definition äquivalent seien. Heutzutage bevorzugt man die
globale Definition.
Der bekannteste archimedische Körper ist der klassische Fußball, begrenzt
durch 12 reguläre Fünfecke und 20 reguläre Sechsecke.
Näheres unter http://de.wikipedia.org/wiki/Archimedische_K%C3%B6rper
V = a³ * 2 * (1 +
2 ) + a³ *
2 + 2 * a³ + a³ *