Zentrische Streckung und Ähnlichkeit
Werbung
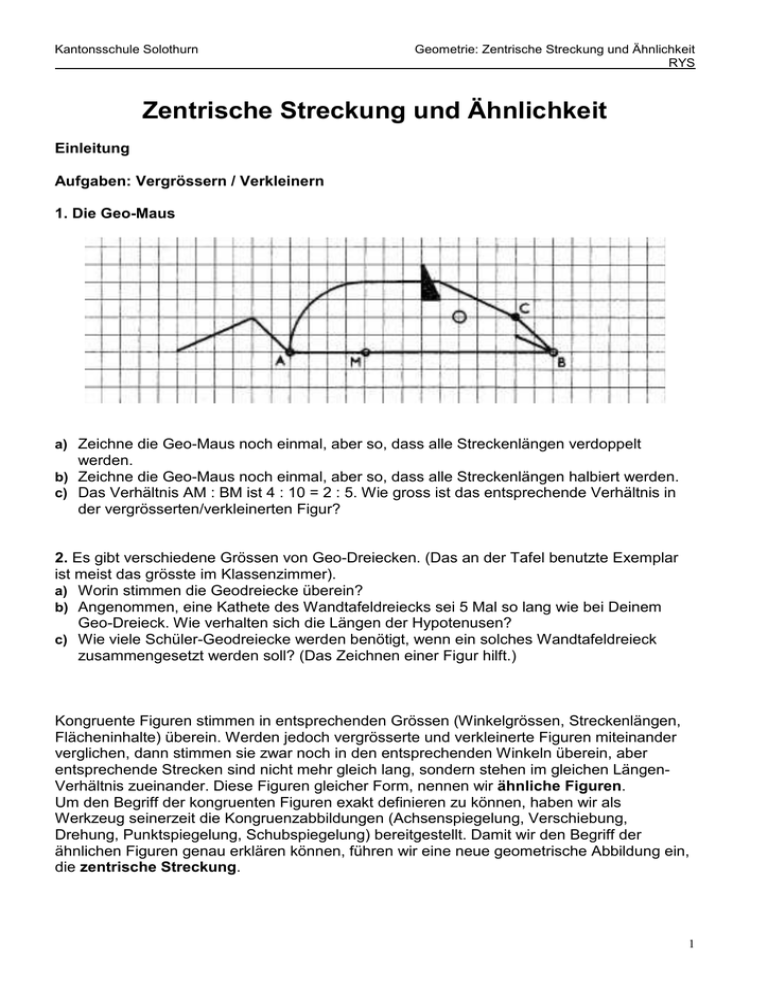
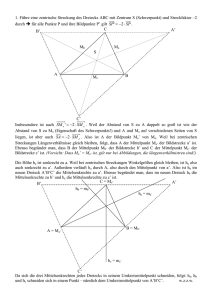
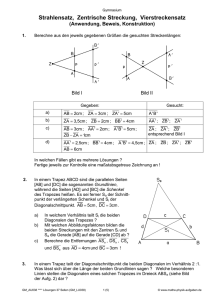
Kantonsschule Solothurn Geometrie: Zentrische Streckung und Ähnlichkeit RYS Zentrische Streckung und Ähnlichkeit Einleitung Aufgaben: Vergrössern / Verkleinern 1. Die Geo-Maus a) Zeichne die Geo-Maus noch einmal, aber so, dass alle Streckenlängen verdoppelt werden. b) Zeichne die Geo-Maus noch einmal, aber so, dass alle Streckenlängen halbiert werden. c) Das Verhältnis AM : BM ist 4 : 10 = 2 : 5. Wie gross ist das entsprechende Verhältnis in der vergrösserten/verkleinerten Figur? 2. Es gibt verschiedene Grössen von Geo-Dreiecken. (Das an der Tafel benutzte Exemplar ist meist das grösste im Klassenzimmer). a) Worin stimmen die Geodreiecke überein? b) Angenommen, eine Kathete des Wandtafeldreiecks sei 5 Mal so lang wie bei Deinem Geo-Dreieck. Wie verhalten sich die Längen der Hypotenusen? c) Wie viele Schüler-Geodreiecke werden benötigt, wenn ein solches Wandtafeldreieck zusammengesetzt werden soll? (Das Zeichnen einer Figur hilft.) Kongruente Figuren stimmen in entsprechenden Grössen (Winkelgrössen, Streckenlängen, Flächeninhalte) überein. Werden jedoch vergrösserte und verkleinerte Figuren miteinander verglichen, dann stimmen sie zwar noch in den entsprechenden Winkeln überein, aber entsprechende Strecken sind nicht mehr gleich lang, sondern stehen im gleichen LängenVerhältnis zueinander. Diese Figuren gleicher Form, nennen wir ähnliche Figuren. Um den Begriff der kongruenten Figuren exakt definieren zu können, haben wir als Werkzeug seinerzeit die Kongruenzabbildungen (Achsenspiegelung, Verschiebung, Drehung, Punktspiegelung, Schubspiegelung) bereitgestellt. Damit wir den Begriff der ähnlichen Figuren genau erklären können, führen wir eine neue geometrische Abbildung ein, die zentrische Streckung. 1 Die Zentrische Streckung Definition Die zentrische Streckung ZS,k mit dem Streckzentrum S und dem Streckfaktor k ordnet jedem Punkt P der Ebene einen Bildpunkt P‘ nach folgender Vorschrift zu: • Zeichne die Gerade (PS). • P‘ liegt auf (PS). • Es gilt P' S = k · PS . • Ist k> 0, so liegen P und P‘ auf der gleichen Seite von S aus gesehen, andernfalls auf verschiedenen Seiten. 2 Kantonsschule Solothurn Geometrie: Zentrische Streckung und Ähnlichkeit RYS Bei der zentrischen Streckung gelten folgende Vereinbarungen: ♦ A, B, C, D sind die Urbildpunkte bzw. bilden das Urbild ♦ A‘, B‘, C‘, D‘ sind die Bildpunkte bzw. bilden die Bildfigur Regel: Urbildpunkt und Bildpunkt liegen zusammen mit dem Streckungszentrum Z auf einer Geraden im Abstand k = P' Z : PZ (k = Streckungsfaktor). 3 Übung Strecke das Dreieck ABC von Z aus mit den Faktoren a) 2 b) 0.5 c) 1 d) -2 e) -0.5 f) -1 4 Kantonsschule Solothurn Geometrie: Zentrische Streckung und Ähnlichkeit RYS Eigenschaften der zentrischen Streckung: ♦ Geradentreu: Aus einer Geraden wird bei der zentrischen Streckung eine BildGerade. ♦ Verhältnistreu: Die Urbildstrecken stehen im selben Verhältnis zueinander wie die Bildstrecken. ♦ Parallelentreu: Sind die Urbild-Linien zueinander parallel so sind auch die BildLinien parallel zueinander. ♦ Winkeltreu: Urbild-Winkel und Bild-Winkel sind bei der zentrischen Streckung immer gleich gross. ♦ Orientierungstreu: Der Drehsinn bleibt bei der zentrischen Streckung erhalten. ♦ Fixpunkte: Bei einer zentrischen Streckung mit k ≠ 1 ist Z der einzige Fixpunkt, jede Gerade durch Z ist Fixgerade. Für k = 1 ist jeder Punkt Fixpunkt und jede Gerade Fixgerade. Übungen: 1. Zeichne das Dreieck ABC mit A(3|2), B(8|3), C(5|6). Konstruiere das Bilddreieck der zentrischen Streckung mit Z (6|4) und k = 1.6. 2. Die Punkte P(7|7) und Q(7|4.5) haben bei einer zentrischen Streckung die Bildpunkte P‘(4|4) und Q‘(4|3). a) Trage die Punkte in ein Koordinatensystem ein und bestimme das Streckungszentrum. b) Bestimme rechnerisch den Streckungsfaktor k. c) Ist A‘(3|2) der Bildpunkt von A(5|2) bei dieser Streckung? Begründe. 3. Gibt es eine zentrische Streckung mit Streckungszentrum Z und Streckungsfaktor k, die A auf A‘ und zugleich B auf B‘ abbildet? Wenn ja, bestimme zeichnerisch die Koordinaten von Z und berechne k; wenn nein, begründe deine Antwort. a) A(3|3), A‘(5|5), B(- 2|0), B‘(- 4|2) b) A(1| - 3), A‘(4|1), B(7|2), B‘(7|5) 4. Stimmt das? Begründe die Aussage oder widerlege sie: a) Eine Punktspiegelung ist auch eine zentrische Streckung. b) Bei gewissen zentrischen Streckungen ändert sich der Orientierungssinn vom Original zum Bild eines Dreiecks. c) Verknüpft man die zentrische Streckung mit dem Zentrum Z und dem Faktor k = 3/8 mit der zentrischen Streckung mit dem gleichen Zentrum Z und k = 8/3 (Kehrwert), dann sind bei dieser Abbildung alle Punkte der Ebene Fixpunkte. d) Auch Kongruenzabbildungen sind winkeltreu. e) Bei zentrischen Streckungen gibt es weder Fixgeraden noch Fixpunkte. 5 5. Ein Dreieck mit a = 14cm, α = 60° und ha =5cm wird auf ein Dreieck mit dem Flächeninhalt 210 cm2 abgebildet. Wie gross sind a‘,α‘ und ha‘ in diesem Dreieck? 6. Zeichne ein Quadrat mit Seitenlänge 3. Strecke es so, dass sich sein Flächeninhalt verdoppelt. 7. Zentrische Streckungen lassen sich auch im Raum durchführen. Mit Schrägrissen können wir sie darstellen: a) Wie gross ist k? Wie gross ist das Volumen des Bildes, wenn die Seitenlänge des Originals 3 cm ist? b) Zeichne den Schrägriss des gestreckten Würfels für k = 3. c) Zeichne das Bild des Schrägrisses bei einer zentrischen Streckung mit k = 2. 6 Kantonsschule Solothurn Geometrie: Zentrische Streckung und Ähnlichkeit RYS KONSTRUKTIONSAUFGABEN Einstiegsaufgabe: Konstruiert werden soll ein Rechteck mit der Diagonalen e = 5 cm, dessen Seiten sich wie 3 : 1 verhalten. Lösung: Wir zeichnen ein Hilfsrechteck, das 3-mal so lang wie breit ist. Dann strecken wir es von der Mitte (oder von einer Ecke) aus so, dass die neue Diagonale 5 cm lang ist. Konstruktionsaufgaben lassen sich oft so lösen, dass • zunächst eine Hilfsfigur mit den richtigen Seitenverhältnissen aber noch nicht der korrekten Grösse gezeichnet wird und dann • die Hilfsfigur zentrisch gestreckt wird. 8. Konstruiere ein Dreieck aus a : ha =6 : 5 ; γ = 60°. und wβ = 5cm 9. Konstruiere ein Dreieck aus a : wγ =6:5, γ =60°. und b=6cm. 10. Konstruiere ein Dreieck mit α = 50°. , γ = 70°. und hb =7cm. 11. Konstruiere ein Dreieck aus a : sc = 9 : 10, β = 55°. und hc =5cm. 12. Konstruiere ein gleichseitiges Dreieck mit sc =5cm. 13. Konstruiere ein gleichschenklig-rechtwinkliges Dreieck mit sa = 6cm. 14. Konstruiere ein Dreieck mit α = 45°, β = 60°. und Umkreisradius r =4cm. (Hinweis: Der Mittelpunkt des Umkreises ist der Schnittpunkt der Mittelsenkrechten.) 15. Konstruiere ein Dreieck mit α = 50°. und β = 60°. und Inkreisradius r =3cm. (Hinweis: Der Mittelpunkt des Inkreises ist der Schnittpunkt der Winkelhalbierenden des Dreiecks. Der Radius des Kreises kann mit dem Geodreieck von der Seite senkrecht zum Schnittpunkt gemessen werden.) 16. Konstruiere ein gleichseitiges Dreieck mit Umkreisradius r =4cm. (Hinweis: Der Mittelpunkt des Umkreises ist der Schnittpunkt der Mittelsenkrechten.) 17. Konstruiere ein gleichschenklig-rechtwinkliges Dreieck mit Inkreisradius r = 3cm. . (Hinweis: Der Mittelpunkt des Inkreises ist der Schnittpunkt der Winkelhalbierenden des Dreiecks. Der Radius des Kreises kann mit dem Geodreieck von der Seite senkrecht zum Schnittpunkt gemessen werden.) 18. Beweise den folgenden Satz: In einem Dreieck schneiden sich die drei Seitenhalbierenden in einem Punkt S. (Schwerpunkt). S teilt jede Seitenhalbierende im Verhältnis 2:1.Werden alle Fusspunkte von Seitenhalbierenden miteinander verbunden, so wird das ursprüngliche Dreieck in vier kongruente Dreiecke zerlegt. 7 Ähnlichkeit Eine Abbildung, die sich zusammensetzt aus einer oder mehreren zentrischen Streckungen und Kongruenzabbildungen, heisst Ähnlichkeitsabbildung. Figuren, die durch eine Ähnlichkeitsabbildung auseinander hervorgehen, nennen wir ähnliche Figuren: F1 ∼ F2. 19. Welche der folgenden Figuren sind zueinander ähnlich? 20. Den Kongruenzsätzen am Dreieck entsprechen Ähnlichkeitssätze. Stelle die Kongruenzsätze am Dreieck zusammen: sss, sws, ssw, sww. Formuliere die entsprechenden Ähnlichkeitssätze. 21. Mit den zentrischen Streckungen habt ihr eine neue Art von geometrischen Abbildungen kennengelernt. Es gibt aber zentrische Streckungen, die gleichzeitig Kongruenzabbildungen sind. Hier sind vier Faktoren von zentrischen Streckungen angegeben. Welche davon bezeichnen auch Kongruenzen: k=-1 ;k=0 ; k= 1 ; k=2 22. Können zwei Dreiecke ABC und A’B’C’ mit den folgenden Daten zueinander ähnlich sein? Begründe Deine Antwort. a) a = 4cm, b = 2,6cm, γ = 40°. und a‘ = 10cm, b‘= 6,7cm und γ‘ = 40°. b) a = 4cm, b = 2,6cm, γ = 40°. und a‘ = 10,5cm, b‘ = 6,5cm und γ‘ = 40°. c) a = 4cm, b = 2,4cm, γ = 40°. und a‘ = 10cm, b‘ = 6,5cm und γ‘ = 40°. d) a = 4,2cm, b = 2,6cm, γ = 40°. und a‘ = 10cm, b‘ = 6,5cm und γ‘ = 40°. 8 Kantonsschule Solothurn Geometrie: Zentrische Streckung und Ähnlichkeit RYS 23. Beweise: In einem Dreieck mit den Seitenlängen a, b und c und den Höhen ha, hb und hc gilt: b : ha =a : hb. (Tipp: die Ähnlichkeitssätze am Dreieck helfen.) 24. In einem Dreieck gilt a : ha = 5 : 2und b : c = 3 : 2. Der Flächeninhalt des Dreiecks beträgt 60 cm2 . Berechne die Länge der Seite a. (Tipp: es braucht nichts konstruiert zu werden.) 25. Konstruiere ein Dreieck aus hc : a : b =3 : 8 : 3,5 mit ha =3cm. (Senkrechte auf Geraden durch bekannte Punkte und Parallelen zu Geraden dürfen mit dem Geodreieck gezogen werden.) 26. Gegeben ist (siehe Bild) ein rechtwinkliges Dreieck mit rechtem Winkel bei C. Die Punkte Ma , Mb und Mc sind die Seitenmittelpunkte, Hc ist der Höhenfusspunkt der Seite c. Die Punkte D und E sind die eingezeichneten Schnittpunkte. a) Welche der Dreiecke McMbMa und DEMa und McHcE sind zueinander ähnlich? Begründe mit den Ähnlichkeitssätzen. b) Wie lang ist DMa, wenn bekannt ist, dass HcB =2cm? Begründung? c) Wie gross ist die Fläche von DEMa , wenn bekannt ist, dass HcB = 2cm und CHc = 2,8cm? 27. Wie gross ist der Flächeninhalt des Trapezes ABED? Die Strecke AD hat die Länge 4,4 cm, die Strecke DE ist 6 cm lang. Das Dreieck DEC hat die Fläche 9.9 cm2. (Vorsicht: Die Längenverhältnisse in der Zeichnung entsprechen nicht diesen Angaben). 28. M1, M2 und M3 sind Seitenmittelpunkte des Rechtecks ABCD. Welchen Bruchteil des Rechteckinhaltes macht der Inhalt der punktierten Fläche aus? 9 29. Berechne die fehlenden Längen. (Seiten auf gestrichelten Geraden sind parallel.) 30. Berechne die Länge der restlichen Abschnitte in dieser Figur: 10