A08015-Zentrische Streckung - Anwendungen 2

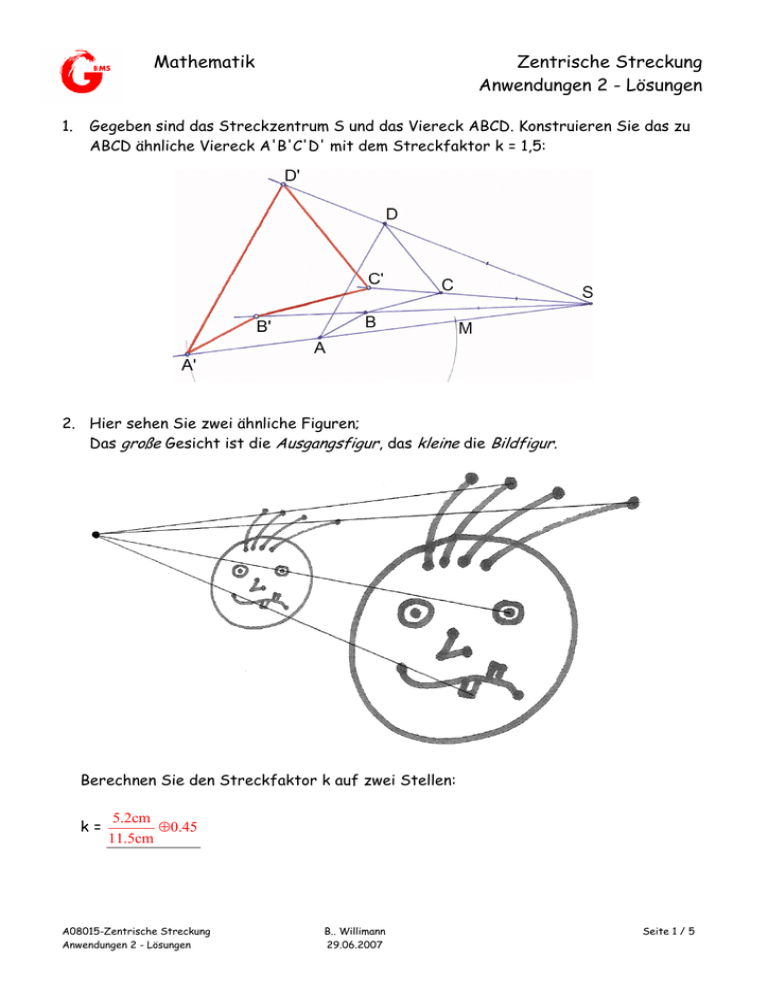
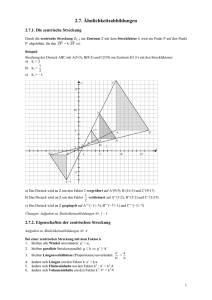
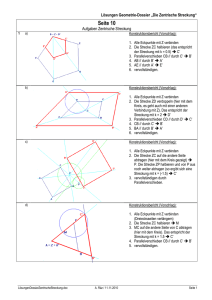
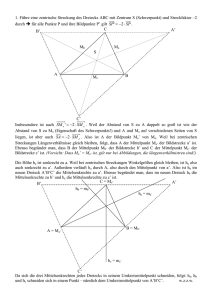
Mathematik
1.
Zentrische Streckung
Anwendungen 2 - Lösungen
Gegeben sind das Streckzentrum S und das Viereck ABCD. Konstruieren Sie das zu
ABCD ähnliche Viereck A'B'C'D' mit dem Streckfaktor k = 1,5:
2. Hier sehen Sie zwei ähnliche Figuren;
Das große Gesicht ist die Ausgangsfigur, das kleine die Bildfigur.
Berechnen Sie den Streckfaktor k auf zwei Stellen:
k=
5.2cm
≈ 0.45
11.5cm
A08015-Zentrische Streckung
Anwendungen 2 - Lösungen
B.. Willimann
29.06.2007
Seite 1 / 5
Mathematik
Zentrische Streckung
Anwendungen 2 - Lösungen
3. Hier sehen Sie nochmals zwei ähnliche Figuren;
Das große Gesicht ist die Ausgangsfigur, das kleine die Bildfigur.
Berechnen Sie den Streckfaktor k auf zwei Stellen:
k= −
4.5cm
≈ −0.45
10.1cm
A08015-Zentrische Streckung
Anwendungen 2 - Lösungen
B.. Willimann
29.06.2007
Seite 2 / 5
Mathematik
Zentrische Streckung
Anwendungen 2 - Lösungen
4. Führen Sie eine zentrische Streckung des gegebenen Fünfecks ABCDE am
Streckzentrum S mit dem Streckfaktor k = 2 durch und beschreiben Sie die
Konstruktion in ein paar kurzen Sätzen:
Konstruktionsbeschrieb:
•
•
•
Die Bildpunkte liegen alle auf einem Strahl von S ausgehend durch den Originalpunkt
Da mit k = 2 der Bildpunkt von S doppelt so weit entfernt liegt wie der Originalpunkt,
kann der Bildpunkt wie folgt konstruiert werden:
o Zirkel im Originalpunkt einstecken (in der Zeichnung C)
o Die Strecke CS auf die andere Seite abtragen ergibt C'
Dies kann nun für alle Originalpunkte so gemacht werden. Alternativ kann die Strecke
CD parallel durch C' gezogen werden womit man D' erhält; die Strecke CE kann
parallel durch D' gezogen werden womit man E' erhält. Dies setzt man solange fort
bis die ganze Figur konstruiert ist.
A08015-Zentrische Streckung
Anwendungen 2 - Lösungen
B.. Willimann
29.06.2007
Seite 3 / 5
Mathematik
Zentrische Streckung
Anwendungen 2 - Lösungen
5. Führen Sie eine zentrische Streckung des gegebenen Fünfecks ABCDE am
Streckzentrum S mit dem Streckfaktor k = -2 durch und beschreiben Sie die
Konstruktion in ein paar kurzen Sätzen:
Konstruktionsbeschrieb:
•
•
•
Die Bildpunkte liegen alle auf einem Strahl von S ausgehend durch den Originalpunkt
Da mit k = -2 der Bildpunkt von S doppelt so weit entfernt liegt wie der
Originalpunkt, kann der Bildpunkt wie folgt konstruiert werden:
o Zirkel im Originalpunkt einstecken (in der Zeichnung C)
o Die Strecke CS auf die andere Seite abtragen ergibt C'
Dies kann nun für alle Originalpunkte so gemacht werden. Alternativ kann die Strecke
CD parallel durch C' gezogen werden womit man D' erhält; die Strecke CE kann
parallel durch D' gezogen werden womit man E' erhält. Dies setzt man solange fort
bis die ganze Figur konstruiert ist.
A08015-Zentrische Streckung
Anwendungen 2 - Lösungen
B.. Willimann
29.06.2007
Seite 4 / 5
Mathematik
Zentrische Streckung
Anwendungen 2 - Lösungen
6. Führen Sie eine zentrische Streckung des gegebenen Fünfecks ABCDE am
Streckzentrum S mit dem Streckfaktor k = -1 durch und beschreiben Sie die
Konstruktion in ein paar kurzen Sätzen:
Eine zentrische Streckung mit k = -1 entspricht einer Rotation der Figur um S mit einem
Winkel von 180° oder anders gesagt einer Punktspiegelung
Konstruktionsbeschrieb:
•
•
•
Die Bildpunkte liegen alle auf einer Geraden vom Originalpunkt aus gehend durch S
Da mit k = -1 der Bildpunkt von S gleich weit entfernt liegt wie der Originalpunkt,
kann der Bildpunkt wie folgt konstruiert werden:
o Zirkel in S einstecken
o Die Strecke SA auf die andere Seite abtragen ergibt A'
Dies kann nun für alle Originalpunkte so gemacht werden. Alternativ kann die Strecke
AB parallel durch A' gezogen werden womit man B' erhält; die Strecke BC kann
parallel durch B' gezogen werden womit man C' erhält. Dies setzt man solange fort
bis die ganze Figur konstruiert ist.
A08015-Zentrische Streckung
Anwendungen 2 - Lösungen
B.. Willimann
29.06.2007
Seite 5 / 5