Beweisen lehren: Beweismittel den Schülern offenlegen

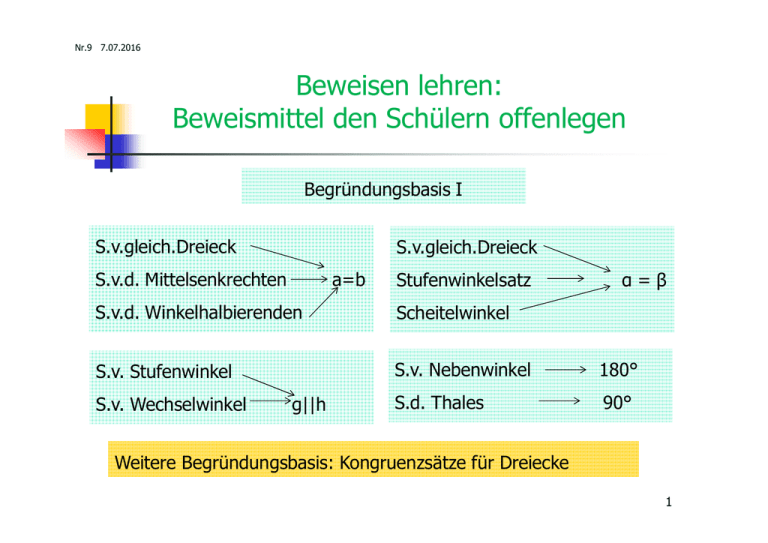
Nr.9 7.07.2016
Beweisen lehren:
Beweismittel den Schülern offenlegen
Begründungsbasis I
S.v.gleich.Dreieck
S.v.gleich.Dreieck
S.v.d. Mittelsenkrechten
a=b
Stufenwinkelsatz
α=β
S.v.d. Winkelhalbierenden
Scheitelwinkel
S.v. Stufenwinkel
S.v. Nebenwinkel
180°
S.d. Thales
90°
S.v. Wechselwinkel
g||h
Weitere Begründungsbasis: Kongruenzsätze für Dreiecke
1
Inhalte: Ähnlichkeitsgeometrie
-
Die zentrische Streckung
Die Strahlensätze
Die Ähnlichkeitssätze für Dreiecke
Sinus/Kosinus/Tangens im rechtwinkligen Dreieck
Der Satz des Pythagoras
Neu: Es geht um Streckenverhältnisse
Frage: Welche Begründungsbasis?
2
Zentrische Streckung
Definition:
Eine Abbildung, die jedem Punkt P einen Punk P´
zuordnet, heißt zentrische Streckung mit dem
Streckzentrum Z und dem Streckfaktor k>0, wenn gilt:
1. P´ liegt auf der von Z ausgehenden Halbgeraden und
2. ZP´= k·ZP
P´
P
Z
3
Zentrische Streckung
Eigenschaften der zentrischen Streckung
Satz: (ohne Beweis)
a) Das Bild einer Gerade ist eine zu ihr parallelen Gerade.
b) Winkel werden auf gleich weite Winkel abgebildet.
c) Strecken werden auf Strecken der k-fachen Länge
abgebildet.
d) Der Flächeninhalt einer Figur wird mit k2 multipliziert.
P´
P
Z
4
Damit beweisen: Strahlensätze
h
g
u
v
Z
y
x
Zeige: Wenn g parallel h, dann u:v = x:y
Beweis: Es gibt eine zentrische Streckung mit Zentrum
Z und Streckfaktor k, die g auf h abbildet. Dann gilt:
y+ x
u
x
k = v +v u = 1 + uv und k = y = 1 + xy , also v = y
5
Strahlensätze
g
h
g
h
u
u
v
y
Z
Z
v
y
x
x
Satz 1:
Wenn g||h, dann verhalten sich Abschnitte auf einem Strahl
wie die entsprechenden Abschnitte auf dem anderen Strahl.
Die Umkehrung von Satz 1 gilt.
6
Strahlensätze
g
u
u
v
y
t
s
Z
h
g
h
s
y
x
Z
t
v
x
Satz 2:
Wenn g||h, dann verhalten sich Abschnitte auf den Parallelen
wie die von Z aus gemessenen entsprechenden Abschnitte
auf einem Strahl.
Die Umkehrung von Satz 2 gilt nicht.
7
Gegenbeispiel
y
s
t
Aus s:t = x:y folgt i.a.
nicht s||t
x
s
y
u
x
t
Ist s:t = x:y und s:t = u:v,
dann folgt s||t
v
8
Ähnlichkeit
Definition:
Zwei Figuren heißen ähnlich, wenn man die eine Figur mit
einer zentrischen Streckung so abbilden kann, dass sie zu
der anderen Figur kongruent ist.
Folgerung
In ähnlichen Figuren haben
- Entsprechende Winkel die gleiche Weite.
- Entsprechende Strecken das gleiche Längenverhältnis.
9
Ähnlichkeitssätze für Dreiecke
(Nur der wichtigste Satz)
Satz: Wenn zwei Dreiecke drei gleiche Winkel
haben, dann sind sie ähnlich, entsprechende
Seitenverhältnisse sind also gleich.
Und die Umkehrung
Satz: Wenn bei zwei Dreiecken entsprechende
Seitenverhältnisse gleich sind, dann sind sie
ähnlich, also sind die Winkel gleich.
10
Sehnensatz
Zeige: a·b = x·y
Wie kommt man auf eine
Beweisidee?
→ Zu zeigen ist ein
Streckenverhältnis a:x = y:b
→ In Frage kommt:
Strahlensätze
Ähnliche Dreiecke
b
y
x
A
a
B
11
Sehnensatz
C
Zeige: a:x = y:b
Beweis:
1. α = α* (Scheitelwinkel)
2. γ = γ* (Umfangswinkel über AB)
3. ▲AZC und ▲DZB haben gleiche
Innenwinkel (Winkelsumme)
4. ▲AZC und ▲DZB sind ähnlich
γ
b
x
A
α Z y γ*
α*
D
a
B
(Ähnlichkeitssatz für Dreiecke)
5. a:x = y:b
(Ähnlichkeitssatz für Dreiecke)
12
S. d. Pythagoras (ca.550 v.Ch.)
C
Satz: Wenn γ = 90°, dann
a2 + b2 = c2.
Die Umkehrung gilt
ebenfalls.
90°
a
b
A
a
B
13
Satzgruppe. d. Pythagoras
Analyse: Das Dreieck ABC
ist ähnlich zu ▲AHC und
▲HBC.
C
90°
γ1 γ2
a
b
Höhe h
1. Kathetensätze
b2 = p·c und a2 = q·c
A
2. Höhenssatz h2= p·q
α
p
q
H
β
B
c
3. Aus 1. folgt a2 + b2 = c2
14
Verallgemeinerung des S. d. Pythagoras
A2
A1
A3
A2
A1
A3
Zeichnet man über die Seiten eines
rechtwinkligen Dreiecks ähnliche
Figuren, dann ist der Flächeninhalt
der Figuren über den Katheten
gleich dem Flächeninhalt der Figur
über der Hypotenuse.
Beweis:
A₁:A₃ = a2:c2 und
A₂:A₃ = b2:c2
Also (A₁+A₂): A₃
= (a2+b2):c2 = 1
D.h. A₁+A₂ = A₃
15
Euklidischer Beweis, Euklid Erstes Buch §47
E
b
C
a
F
b
A
D
c
p
H
B
Idee
„Flächenverwandlung“
Man zeigt:
Die Dreiecke AHD und ACF
haben denselben Inhalt.
(Kathetensatz)
G
AHD = AHC (Grundseite und Höhe gleich)
= ABF (Drehung um A mit 90°)
= ACF (Grundseite und Höhe gleich)
16