Formelblätter Physik
Werbung

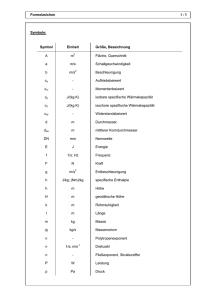
Formeln und Tafeln für die Schweizerischen Maturitätsprüfungen, Physik (Grundlagenfach) Neue Richtlinien, Version Dezember 2008 (Revisionen vorbehalten) Spezielle Daten, die hier nicht vorkommen und die nicht als Allgemeinwissen vorausgesetzt werden können, werden im Rahmen der Aufgaben angegeben. Tabelle I: Grössen, ihre Formelzeichen und ihre Einheiten Formelzeichen werden kursiv, Einheiten gerade gedruckt. Formelzeichen Einheit (falls eigene Einheit) Einheit kurz Arbeit W Joule, Kilowattstunde J, kWh Beschleunigung a m/s Dichte ρ kg/m Druck p Elektrische Feldkonstante ε0 Elektrische Ladung Q Coulomb C Elektrische Spannung U Volt V Elektrische Stromstärke I Ampere A Energie E Joule, Kilowattstunde Federkonstante D Fläche A Quadratmeter m Frequenz f Hertz Hz Geschwindigkeit v Kraft F Newton N Leistung P Watt W Masse m Kilogramm kg Ohmscher Widerstand R Ohm Ω Periodendauer T Sekunde s Stoffmenge n mol Grösse Strecke s, ℓ T (ϑ) Temperatur Volumen V Wellengeschwindigkeit c Pascal, Bar Basisgrösse des SI 2 3 Pa, bar . C/(V m) + J, kWh N/m 2 m/s, km/h Meter Kelvin, Grad Celsius Kubikmeter + mol + m + K, °C + m 3 m/s Winkelgeschwindigkeit ω (Sekunde) Zeit t Sekunde -1 s -1 s Formales Verwendung eckiger Klammern Eckige Klammern [ ] werden gelesen als „Einheit von“. Beispiele: [F] = N bedeutet: Die Einheit der Kraft ist Newton. [v] = m/s bedeutet: Die Einheit der Geschwindigkeit ist Meter pro Sekunde. Eckige Klammern rahmen also stets ein Formelzeichen ein, nie eine Einheit. -1- + Bezeichnung von Achsen in grafischen Darstellungen Die Achsen werden mit dem Formelzeichen der gemessenen Grösse bezeichnet. Abgetrennt durch einen Bruchstrich wird die verwendete Einheit angegeben. Um Unklarheiten zu vermeiden, kann eine zusammengesetzte Einheit, z.B. m/s m m auch so geschrieben werden: , also v / , s s Oberes Beispiel: Hier ist eine Höhe h als Funktion der Zeit t qualitativ dargestellt. Eine Angabe von Einheiten erübrigt sich. Unteres Beispiel: Hier ist ein zeitlicher Temperaturverlauf quantitativ dargestellt. Als Temperatureinheit werden °C verwendet, als Zeiteinheit Stunden. Die Skalen gestatten ein genaues Abmessen einzelner Kurvenpunkte. Symbole für elektrische Stromkreise (a) (b) (c) Elektrische Leitungen (a) Abzweigung (b) Kreuzung ohne Berührung (c) Kreuzung mit Berührung Widerstand, Verbraucher Lampe Schalter Spannungsquelle -2- Tabelle II: Wichtige chemische Elemente Ordnungszahl Z Massenzahl A Helium 2 4 Kohlenstoff 6 12 Sauerstoff 8 16 Stickstoff 7 14 Wasserstoff 1 1 Element Tabelle III: Wichtige Konstanten Konstante Wert Formelzeichen . -27 u 1.66 10 Avogadro-Konstante NA . Boltzmann-Konstante k Atomare Masseneinheit . ε0 Elementarladung e -23 J/K -12 C/(V m) . . -19 -11 3 8.85.10 1.60 10 . G, f, γ Gravitationskonstante -1 6.02 10 mol 1.38 10 Elektrische Feldkonstante kg 23 6.67 10 . C . 2 m /(kg s ) -34 . Plancksches Wirkungsquantum h 6.63 10 Universelle Gaskonstante R 8.31 J/(mol K) Vakuumlichtgeschwindigkeit* co 3.0 10 m/s Js . . 8 * Die Lichtgeschwindigkeit in Luft weicht nur geringfügig von der Vakuumlichtgeschwindigkeit ab, so dass zwischen den beiden Werten normalerweise nicht unterschieden werden muss. Tabelle IV: Häufig benutzte Zahlenwerte Formelzeichen Wert Fallbeschleunigung g 9.81 m/s ≈ 10 m/s Schallgeschwindigkeit in Luft cL 340 m/s Normdruck po 1.0 bar = 1.0 10 Pa Absoluter Nullpunkt To 0 K = -273°C *) Grösse 2 . 2 5 *) Temperaturmessungen sind oft recht ungenau. Deshalb ist es sinnlos, hier Kommastellen anzugeben. Tabelle V: Vorsätze Beachten Sie die Gross- und Kleinschreibung! Pico Nano Mikro Milli Zenti Dezi Deka Hekto Kilo Mega Giga Tera p n µ m c d da h k M G T 10-12 10-9 10-6 10-3 10-2 10-1 101 102 103 106 109 1012 -3- Tabelle VI: Häufig gebrauchte griechische Buchstaben Aussprache klein Alpha Phi α β γ δ ε η λ µ µ ω ϕ Pi π 3.14… Rho ρ ϑ Dichte, spez. Widerstand Beta Gamma Delta Epsilon Eta Lambda Mü Omega Theta Verwendung z.B. für gross Verwendung z.B. für Winkel, linearer Ausdehnungskoeffizient Winkel Volumen-Ausdehnungskoeffizient Differenz, Zuwachs ∆ Differenz, Zuwachs Ω Einheit Ohm Elektrostatik: Feldkonstante Wirkungsgrad Wellenlänge Mikro, Reibungskoeffizient Winkelgeschwindigkeit Drehwinkel Formelzeichen für Celsius-Temperatur Tabelle VII: Materialgrössen Spezifische Wärmekapazität von Wasser cW = 4.18 kJ/kgK Spezifische Wärmekapazität von Eis cE = 2.10 kJ/kgK Schmelzwärme von Eis Lf = 334 kJ/kg Verdampfungswärme von Wasser Lv = 2257 kJ/kg Dichte von Wasser ρW = 1.0.103 kg/m3 Formeln und Definitionen Die Formelzeichen werden nicht einzeln erklärt. Sie entsprechen den allgemeinen Gepflogenheiten und sind grossenteils in der Tabelle I definiert. Grundlagen Definition: Dichte ρ = m V Mechanik Definition: Geschwindigkeit v = ∆s ∆t ; Beschleunigung a= ∆v ∆t Formeln für gleichmässig beschleunigte Bewegung: 1 v(t ) = v0 + a ⋅ t ; s (t ) = s0 + v0 ⋅ t + a ⋅ t 2 2 Zentripetalbeschleunigung: az = ; 2 ⋅ a ⋅ s = vE2 − v02 v2 4π 2 2 = r ⋅ ω 2 = r ⋅ ( 2π ⋅ f ) = r ⋅ 2 r T -4- Kraft: F = m ⋅ a ; Arbeit: W = Fs ⋅ s ; Leistung: Normalkraft: F⊥ = m ⋅ g ⋅ cos α P = W / t = Fs ⋅ v Hangabtriebskraft: F = m ⋅ g ⋅ sin α Reibungskraft: FR = µ ⋅ F⊥ Federkraft: FF = − D ⋅ ∆ℓ Hubarbeit: W = m ⋅ g ⋅ ∆h ; Beschleunigungsarbeit: W = Arbeit beim Spannen einer Feder: WF = m 2 2 ⋅ ( v2 − v1 ) 2 D ⋅ ∆ℓ 2 2 potentielle Energie: E p = m ⋅ g ⋅ h ; kinetische Energie: Ek = potentielle Energie einer gespannten Feder: EF = D ⋅ ∆ℓ 2 2 FG = −G ⋅ Gravitation: 1 m ⋅ v2 2 m1 ⋅ m2 r2 Impuls: p = m ⋅ v Druck ( Definition ) : p = F ; Schweredruck: p = ρ Fl ⋅ g ⋅ h A FA = ρ Fl ⋅ VVerd ⋅ g Auftriebskraft: Wärmelehre Thermische Ausdehnung: linear: ∆ℓ = ℓ ⋅ α ⋅ ∆T ; Volumen: ∆V = V ⋅ γ ⋅ ∆T (Flüssigkeiten) ; ∆V = V ⋅ 3α ⋅ ∆T (festeStoffe) Energie: Erwärmung/Abkühlung: ∆Q = m ⋅ c ⋅ ∆T ; Schmelzen/Erstarren: ∆Q = m ⋅ L f Verdampfen/Kondensieren: ∆Q = m ⋅ Lv ; Verbrennen: ideales Gas: ∆Q = m ⋅ H p ⋅V = n ⋅ R ⋅ T Schwingungen und Wellen HarmonischeSchwingung: y (t ) = yˆ ⋅ sin ( 2π ft + ϕo ) v(t ) = yˆ ⋅ 2π f ⋅ cos ( 2π ft + ϕo ) 2 a(t ) = − yˆ ⋅ ( 2π f ) ⋅ sin ( 2π ft + ϕo ) Zusammenhang Wellenlänge - Frequenz - Wellengeschwindigkeit: λ ⋅ f = c -5- c ± vB c ∓ vS sin α1 c1 n2 Brechungsgesetz: = = sin α 2 c2 n1 Dopplereffekt: f B = f S ⋅ Abbildungsgleichungen: 1 1 1 B b + = = ; b g f G g Definition: Brechzahl eines Materials nM = co cM Elektrizitätslehre Coulomb-Gesetz: Fc = 1 4 ⋅π ⋅ε 0 Ohmsches Gesetz: ⋅ Q1 ⋅ Q2 r2 U =R I n n −1 Parallelschaltung: RErs = ∑ Ri−1 ; Serieschaltung: RErs. = ∑ Ri i =1 i =1 Elektrische Leistung: P = U ⋅ I = U2 = I2 ⋅R R Widerstand eines Drahtes: R = ρ ⋅ℓ A mit ρ = spez. Widerstand, ℓ = Länge, A = Querschnittsfläche Moderne Physik Energie eines Lichtquants: E = h ⋅ f Aequivalenz Masse - Energie: E = m ⋅ c2 Geometrie Kreisumfang: u = 2 ⋅ π ⋅ R = π ⋅ D ; Kreisfläche: A = R2 ⋅π = Kugeloberfläche: A = 4 ⋅ π ⋅ R 2 = π ⋅ D 2 ; Kugelvolumen: V = dünner Ring ( d ≪ D ) : A ≈ π ⋅ D⋅d dünnwandiger Zylinder ( d ≪ D ) : V ≈ π ⋅ D ⋅ d ⋅ h dünnwandige Hohlkugel ( d ≪ D ) : V ≈ π ⋅ D 2 ⋅ d Kegel und Pyramide: V = -6- A⋅ h 3 D2 ⋅π 4 4 ⋅π 3 π ⋅ R = ⋅ D3 3 6 Die Formeln für die Flächenberechnung von Dreiecken, Parallelogrammen und Trapezen sowie die Volumenberechnung von Quadern und Prismen werden als bekannt vorausgesetzt, ebenso der pythagoreische Lehrsatz sowie die Anwendung der Winkelfunktionen. Die Zusammenhänge Frequenz – Winkelgeschwindigkeit oder Kreisfrequenz – Periodendauer (f – ω – T) werden als bekannt vorausgesetzt. Die allgemein gebräuchlichen Formelzeichen sind in Tabelle 1 aufgelistet. Bei in der Formelsammlung vorkommenden speziellen Formelzeichen gehen wir davon aus, dass sie im Verlauf des Unterrichts vom Lehrer erklärt werden. Es soll damit vermieden werden, dass die Formelsammlung mit allzu viel Text zu belastet wird. Diese letzte Seite wird an der Prüfung nicht abgegeben. -7-