Winkel bis 180° mit dem Geodreieck zeichnen

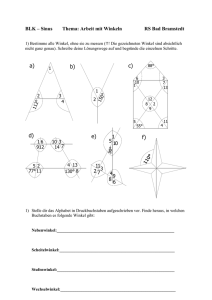
Winkel bis 180° mit dem Geodreieck
zeichnen
9
Aufgabe 1
Unten siehst du zwei Anleitungen zum Zeichnen von Winkeln bis 180°. Leider ist dabei sowohl die Reihenfolge der Texte als auch die Reihenfolge der Bilder durcheinandergeraten. Bringe die Texte und
Bilder wieder in die richtige Reihenfolge.
✕
a)
Gewünschten Winkel an der Winkelskala markieren.
✕
S
53˚
✕
Geodreieck auf den Scheitelpunkt des Winkels legen.
S ✕
Winkelbogen einzeichnen und Winkelgröße eintragen.
S✕
Markierungspunkt mit dem Scheitelpunkt verbinden.
b)
S✕
✕
Scheitelpunkt und einen Schenkel des Winkels zeichnen.
S
✕
(1)
(1)
Zweiten Schenkel des Winkels zeichnen.
✕
S
S✕
Geodreieck auf den Scheitelpunkt des Winkels legen.
Winkelbogen einzeichnen und Winkelgröße eintragen.
✕
S
53˚
S ✕
Scheitelpunkt und einen Schenkel des Winkels zeichnen.
S ✕
Geodreieck bis zum gewünschten Winkel drehen.
Aufgabe 2
Ergänze den Schenkel nach oben und nach unten, sodass je zweimal der angegebene Winkel entsteht.
a) 30°
b) 75°
c) 112°
d) 152°
Aufgabe 3
Zeichne jeweils einen Winkel mit der angegebenen Größe in dein Heft.
a) 20°
b) 43°
c) 66°
Michael Körner: Grundwissen Ebene Geometrie
© Persen Verlag
d) 95°
e) 135°
f) 164°
g) 180°
11
Nebenwinkel und Scheitelwinkel
Aufgabe 1
Ergänze den Lückentext mit den angegebenen Wörtern. Achte auf die Zeichnungen.
Einzusetzende Wörter: Scheitelwinkel(paar), Nebenwinkel(paar), Geradenkreuzung
✕
.
Schneiden sich zwei Geraden, so spricht man von einer
Die dabei entstehenden Winkel a1 und a2 werden als
α1
✕
α2
bezeichnet, da sie nebeneinander liegen.
Die Winkel b1 und b2 werden als
bezeichnet.
β1
✕
Aufgabe 2
Kennzeichne
– die Nebenwinkel zu a1 und a2 rot,
– die Scheitelwinkel zu b1 und b2 blau.
✕
α2 ✕
α1
✕
β1
Aufgabe 3
a) Miss jeweils die vier Winkel und notiere ihre Größe.
a1 = _____
β1
γ1
✕
δ1
α1
g1 = _____
b1 = _____
d1 = _____
δ2
✕
γ2
α2 β
2
a2 = _____
b2 = _____
g2 = _____
d2 = _____
b) Notiere alle Nebenwinkelpaare.
c) Was kannst du über die Summe der Größe von Nebenwinkeln aussagen?
d) Notiere alle Scheitelwinkelpaare.
e) Was kannst du über die Größe von Scheitelwinkeln aussagen?
Aufgabe 4
Berechne die Größe der fehlenden Winkel an der Geradenkreuzung.
α
β
γ
✕
δ
a) a = 50°
b = _____
g = _____
d = _____
b) a = _____
b = 75°
g = _____
d = _____
c) a = _____
b = _____
g = 112°
d = _____
d) a = _____
b = _____
g = _____
d = 173°
e) a = 90°
b = _____
g = _____
d = _____
Michael Körner: Grundwissen Ebene Geometrie
© Persen Verlag
β2 ✕
β2
Vermischte Übungen zu Vierecke
konstruieren
44
Aufgabe 1
a) Trage die Punkte
y
A1(2,5 | 3,5), B1(1 | 2,5), C1(2,5 | 0,5),
Parallelogramm
Drachenviereck
4
A2(–1,5 | 0,5), B2(–1 | 2), C2(–4 | 3),
3
A3(–1,5 | –1), B3(–3,5 | –1), C3(–4,5 | –2,5),
2
A4(0,5 | –2), B4(2 | –3), C4(3,5 | –2)
1
in das Koordinatensystem ein.
–4
b) Ergänze die Punkte D1 bis D4, so dass sich die
angegebene Figur ergibt.
S2(__ | __)
S3(__ | __)
–2
–1
1
2
3
4
x
–1
–2
c) Zeichne bei allen Figuren die Diagonalen e1 bis e4 und
f1 bis f4 ein und gib näherungsweise die Koordinaten der
Diagonalenschnittpunkte S1 bis S4 an.
S1(__ | __)
–3
–3
gleichschenkliges
–4
Trapez
S4(__ | __)
Raute
Aufgabe 2
Übertrage die Figuren in dein Heft, zeichne die Höhen ein und gib ihre Längen an.
✕
✕
✕
✕
✕
✕
✕
✕
✕
✕
✕
✕
✕
✕
✕
✕
Aufgabe 3
Konstruiere die gesuchten Figuren. Bestimme die fehlenden Stücke durch Messen. Achtung: Du musst
bei den Konstruktionen teilweise die Eigenschaften der Figuren benutzen.
a) Unregelmäßiges Viereck mit a = 3,9 cm; b = 5,4 cm; c = 2,6 cm; d = 4,7 cm; g = 70°
e = _____
f = _____
a = _____
b = _____
a = g = _____
b = d = _____
d = _____
b) Raute mit a = 6 cm, f = 4 cm
e = _____
ha = _____
c) Drachenviereck mit a = 5,2 cm, b = 2,8 cm, e = 4,6 cm (Symmetrieachse ist BD)
f = _____
a = _____
b = _____
g = _____
d = _____
d) Parallelogramm mit b = 5 cm, hb = 4,2 cm und g = 73°
a = _____
e = _____
e) Quadrat mit f = 6 cm.
a = _____
e = _____
Michael Körner: Grundwissen Ebene Geometrie
© Persen Verlag
f = _____
ha = _____
a = _____
b = d = _____