Beispiel 4 - mathe
Werbung

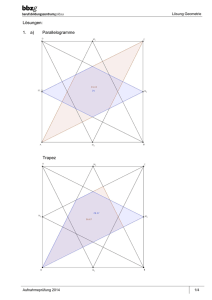
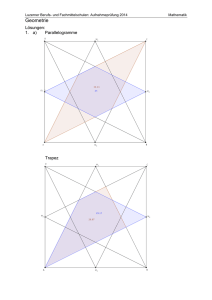
2. Schulaufgabe aus der Mathematik gehalten am 18.01.2010 Klasse 7 Name:_____________________________________ 1. „Es war einmal!“ a) Welche der folgenden Terme beschreiben den Flächeninhalt der gefärbten Fläche zutreffend? Kreuze alle richtigen Terme an. □ □ □ □ □ 2a(a – 2x) – (a – 2x)2 a2 – (4x)2 –(4x2 – a2) 4a – 8x (a – 2x)2 + 4(a – 2x)x ____________________________________________________ ____________________________________________________ ____________________________________________________ ____________________________________________________ ____________________________________________________ __/4 b) Fasse soweit wie möglich zusammen: 10a2 0, 2b4 (2ab2 )2 2 2b(b3a 2 a 2 ) ____________________________________________________ ____________________________________________________ ____________________________________________________ ____________________________________________________ __/3 c) Klammere bei folgendem Term weitestgehend aus: -18b6 + 3b2 – 6b4c = ____________________________________________________ __/2 2. Gleichungen und Lösungsmenge Bestimme die Lösungsmengen folgender Gleichungen, a) 2(2x – 8) (x + 5) = (2x + 8) (2x – 8) + 16x __/3 b) (1 + x)2 = x –x(–1 – x) __/4 2 c) 0,5x + 3x = (x + 2)2 – 2 + x __/4 d) 1 x 1 1 1 x 3 3 2 3 __/4 ___________________________ _________________________ ___________________________ _________________________ ___________________________ _________________________ ___________________________ _________________________ ___________________________ _________________________ ___________________________ _________________________ ___________________________ _________________________ ___________________________ _________________________ ___________________________ _________________________ ___________________________ _________________________ ___________________________ _________________________ ___________________________ _________________________ ___________________________ _________________________ ___________________________ _________________________ ___________________________ _________________________ ___________________________ _________________________ ___________________________ _________________________ ___________________________ _________________________ ___________________________ _________________________ ___________________________ _________________________ ___________________________ _________________________ ___________________________ _________________________ ___________________________ _________________________ ___________________________ _________________________ 3. Textaufgabe Beim Fußballturnier der 7. Klassen werden Frauke, Jochen und Sabine als die drei besten Torschützen ausgezeichnet. Jochen hat 1 Tor weniger als Frauke, Sabine 2 Tore weniger als Jochen erzielt. Die drei haben zusammen die Hälfte der insgesamt 16 Tore geschossen. Wie viele Tore hat jeder der drei erzielt? ____________________________________________________ ____________________________________________________ ____________________________________________________ ____________________________________________________ ____________________________________________________ __/4 4. Vierecke Stimme folgenden Aussagen zu oder widerlege Sie (Begründung/Skizze): a) „Ein Quadrat ist auch ein Drache.“ b) „Ein Drache ist auch ein Trapez.“ c) „Ein Parallelogramm ist auch ein gleichschenkliges Trapez.“ d) „Nur im Quadrat halbieren sich die Diagonalen senkrecht.“ e) „In jedem besonderen Viereck außer dem Trapez sind mindestens zwei Innenwinkel gleich groß.“ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ __/5 5. Grundkonstruktionen Zeichne in folgendes Koordinatensystem die Punkte A(4/2), C (-2/1) und D(2,5/-2). a) Halbiere den Winkel, der durch die Strecken [DA] und [DC] gebildet wird. __/2 __/2 b) Fälle ein Lot von A auf die Strecke [CD]. c) Konstruiere den Punkt B so, dass ein gleichschenkliges Trapez entsteht, __/3 deren parallele Seiten die Strecken [AB] und [CD] sind. y 5 4 3 2 1 -3 -2 -1 O 1 2 3 4 5 x -1 -2 -3 Ergebnis: ___/40