Document

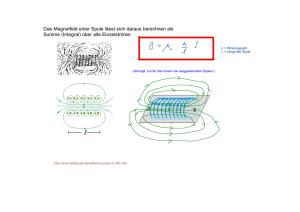
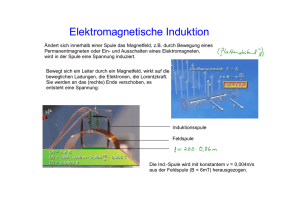
Übungen zur Physik II (Elektrodynamik)
SS 05
11. Übungsblatt
30.06.2005
Bearbeitung bis Mi. 6.07.2005
Aufgabe 1. Lorentzkraft (2+4)
Ein Stab mit der Masse m und dem Ohmschen Widerstand R kann sich reibungsfrei auf zwei
parallelen Schienen bewegen. Zwischen den Schienen , die den Abstand l besitzen , herrsche
ein senkrechtes, homogenes Magnetfeld B . Durch Schließen des Schalters S werde eine
Spannungsquelle mit der Spannung U0 zwischen den Schienen angeschlossen. Die Schienen
haben keinen Widerstand.
a) Berechnen Sie die Kraft auf den Stab als Funktion des Stromes I durch den Stab.
Der Strom fließt von Plus nach negativ , das Magnetfeld zeigt nach oben. Nach der
Rechten Handregel wirkt die Lorentz-Kraft nach rechts, also von den Kontaktstellen weg.
FL = q(v × B) = q ⋅ v ⋅ B
v=
da B senkrecht auf v steht . Mit
I
ρ⋅A
ρ=
und
FL = q
q
folgt
l⋅A
I ⋅l ⋅ A
B = I ⋅l ⋅ B
q⋅ A
b) Bestimmen Sie unter Berücksichtigung der Induktion die Geschwindigkeit vs(t) des Stabs.
Zeigen Sie, dass eine konstante Endgeschwindigkeit ve für t ∞ erreicht wird.
Welcher Strom Ie fließt dann?
Hinweis: Gehen Sie von der Bewegungsgleichung F = mv& aus.
FL =
U
U − U ind
⋅l ⋅ B = 0
⋅ l ⋅ B = m ⋅ v&
R
R
r r
& = − d Bdf
U ind = −Φ
dt ∫
Wegen der Geometrie ist B und F unabhängig voneinander, das Integral vereinfach sich dann
zu :
U ind = −
d
dx
( BF ) = − Bl
= − Blv
dt
dt
einsetzen in die Lorentzkraft:
1
l⋅B
(U 0 − B ⋅ l ⋅ v) = m ⋅ v&
R
l⋅B
l⋅B
v& +
B ⋅l ⋅v −
U0 = 0
m⋅R
m⋅R
FL =
Dies ist eine DGL 1.Ordnung mit konstanten. Mit der AWP v(0)=0 und Trennung der
Veränderlichen folgt:
U0
B 2l 2
v(t ) =
(1 − exp(
t ))
lB
m⋅R
Für t ∞ folgt
ve =
Ie =
U0
lB
Ue 1
U
1
= (U 0 − B ⋅ l ⋅ ve ) = (U 0 − B ⋅ l ⋅ 0 ) = 0
R R
R
l⋅B
Da es keine Reibung gibt , kann für v= const. Keine Kraft wirken.
Augabe 2. Feldspule und Induktion (2+2+2+2)
In einer zylindrische Feldspule, mit Länge l und der Windungszahl N1 die von
einem Strom I1 durchflossen wird, befindet sich eine Induktionsspule. Die Induktionsspule hat
die Windungszahl N2 und einer Windungsfläche A2. In beiden Spulen befindet sich Luft.
a) Wie groß ist der magnetisches Fluss in der Induktionsspule , wenn die Spule ruht und der
Strom I1 konstant ist.
Die Feldspule erzeugt ein homogenes und konstantes Feld . Dieses steht senkrecht auf der
Fläche der Induktionsspule.
r r
A
Φ 2 = ∫ Bdf = B1 A2 = µ 0 N1 I 0 2 = 6,28 ⋅ 10 −7 Wb
l1
b) Berechnen Sie die Gegeninduktivität M der Anordnung.
 dI 
U 2,indu = − M  0 
 dt 
Der Gleichung ist zu entnehmen, dass die Spannung aufgrund einer Stromänderung erfolgt.
Die Änderung des Fluss der Feldspule erzeugt in jeder der N2 Wicklungen der
Induktionsspule die Spannung
U0 = −
2
dΦ 2
dt
Für die Gesamtspannung gilt dann:
dΦ 2
A dI
= − µ 0 N1 N 2 2 1
dt
l1 dt
U 2,indu = − N 2
M = µ 0 N1 N 2
A2
= 5,02 µH
l1
c) Bestimmen Sie die Induktionsspannung U2,indu in Abhängigkeit der Zeit.
Wenn gilt: I1(t)=I0e-t/τ
Hier setzen wir den Strom in das Ergebnis von b) ein:
d
 M
U 2,indu = −M  I 0 exp(− t )  =
I 0 exp(− t )
τ
τ
 dt
 τ
U 0,indu =
M
τ
I 0 = 3,06mV
d) Sei I1 =I0 wieder konstant . Berechnen Sie die induzierte effektive Stromstärke I2,eff , wenn
die Induktionsspule um die Symmetrie Achse S mit der Drehfrequenz f rotiert. Der
Widerstand der Induktionsspule sei R2
Bn = B1 cos(ω ⋅ t ) mit ω = 2π ⋅ f
Φ 2 = Bn A2 = µ 0 N1 I 0
U 2,indu = − N 2
A2
cos(ω ⋅ t )
l1
dΦ 2
= ω ⋅ M ⋅ I 0 sin (ω ⋅ t )
dt
Es liegt also eine Wechselspannung vor.
Die Effektivwert der Spannung und des Stroms sind somit
U indu ,eff =
U indu ,eff =
ω ⋅ M ⋅ I0
2
ω ⋅ M ⋅ I0
2 ⋅ R2
Aufgabe 3. Spule(2)
3
= 22,3mA
Integration über den gezeigten geschlossen Weg mit den Ampereschen Gesetzes.
Die Teile des Pfades außerhalb der Spule trägt nicht bei, da B = 0.
Die beiden Seitenstrecken sind betragsmäßig gleich, haben aber Unterschiedliche Vorzeichen
wegen der Integrationsrichtung. Der einzige Beitrag stammt von dem Teil der parallel zum
Magnetfeld ist:
r r
B
∫ ⋅ ds = B ⋅ L = µ 0 ∑ I =µ 0 NI
C
B = µ0n ⋅ I
Wobei N die Wicklungen sind die vom Pfad eingeschlossen sind.
Aufgabe 4. Koaxial Kabel (3)
Bestimmen die Induktion pro Länge l eines Koaxial Kabels dessen innere Leiter den Radius
r1 und der äußere den Radius r2 hat. Nehmen Sie dazu an, dass die Leiter dünne Hohlzylinder
seinen und mit Luft gefüllt. Die Leiter tragen gleiche gegengesetzte Ströme.
Wir bestimmen den magnetischen Fluss ΦB.
Für das Magnetfeld des inneren Leiters gilt:
B=
µ0 I
2π ⋅ r
Der Fluss durch eine Fläche der Länge l und der Breite dr.
dΦ B = B(l ⋅ dr ) =
µ0 I
l ⋅ dr
2π ⋅ r
Der Gesamte Fluss ist dann:
r2
µ I dr µ 0 I
r
Φ B = ∫ dΦ B = 0 l ∫
=
l ln 2
2π r r
2π
r1
1
Da die Ströme in den Leiter entgegngesetzt gleich sind, haben wir nur eine Schleife.
4
Die Selbstinduktion ist dann
L=
Φ B µ 0l r2
=
ln
I
2π
r1
Für die Induktion pro Länge folgt dann:
L µ 0 r2
=
ln
l 2π r1
Aufgabe 5. LR- Schaltung (1+1+1+1+1)
Ein Widerstand R, 30 Ω, und eine Spule L, 220 mH , seine in Reihe geschaltet. Zum
Zeitpunkt t=0 wird eine 12V Batterie an die Schaltung angeschlossen.
Man berechne:
a) den Strom zum Zeitpunkt t=0
Der Strom ist I = 0. Da die Induktion der Spule dem Strom entgegenwirkt.
b) die Zeitkonstante τ
τ =L/R=7,3 ms
c) den maximalen Strom
Der maximale Strom fließt nach t ∞ . Imax = U/R= 0,4 A
d) die Zeit bis der Strom auf die Hälfte des Maximums angestiegen ist.
-t/τ
Es gilt I = Imax(1-e ) :
½ = (1-e-t/τ)
t = τln2 = 5,0 ms
e) Wie groß ist die Energieänderung ist im Feld im Fall d)
W =
1
 dI 
 dW 
L ⋅ I 12/ 2 
 = LI1 / 2 ⋅  1 / 2 
2
 dt 
 dt 
Es gilt : L
dI
+ RI = U
dt
(DGL)
Daraus folgt:
 dI 
 dW 

 = I1/ 2 ⋅  L 1/ 2  = I1/ 2 (U − IR) = 1,2W
 dt 
 dt 
5
6