Angaben
Werbung
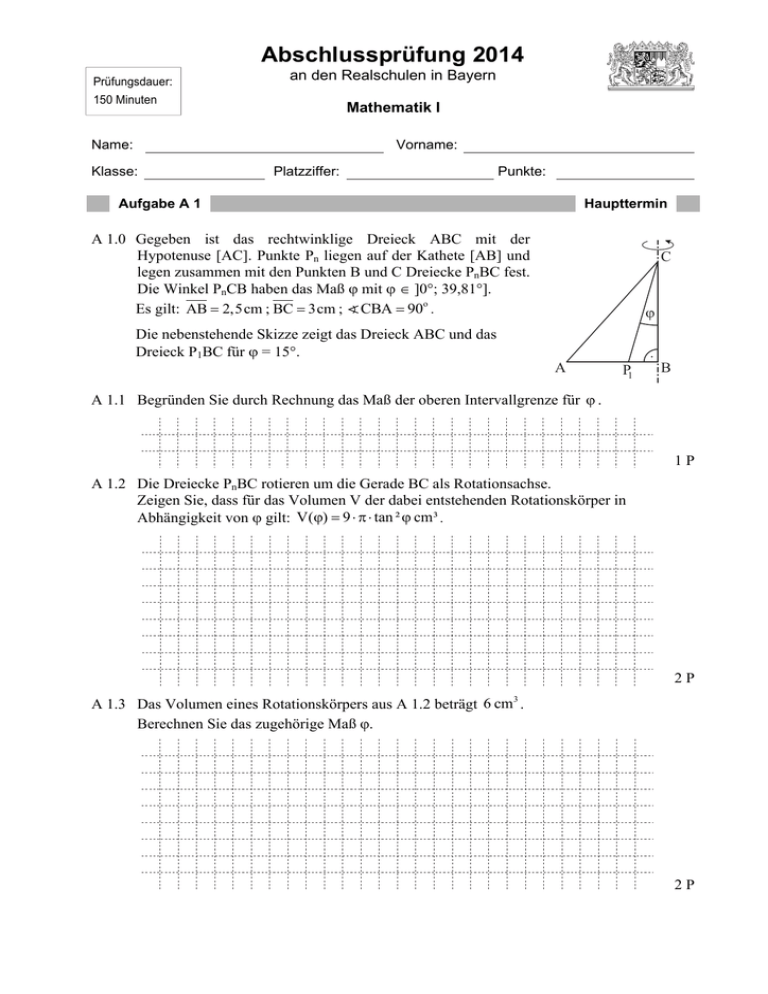
Abschlussprüfung 2014 Prüfungsdauer: 150 Minuten an den Realschulen in Bayern Mathematik I Name: Vorname: Klasse: Platzziffer: Punkte: Aufgabe A 1 Haupttermin A 1.0 Gegeben ist das rechtwinklige Dreieck ABC mit der Hypotenuse [AC]. Punkte Pn liegen auf der Kathete [AB] und legen zusammen mit den Punkten B und C Dreiecke PnBC fest. Die Winkel PnCB haben das Maß mit ]0°; 39,81°]. Es gilt: AB 2,5cm ; BC 3cm ; CBA 90o . Die nebenstehende Skizze zeigt das Dreieck ABC und das Dreieck P1BC für = 15°. C ϕ A P1 . B A 1.1 Begründen Sie durch Rechnung das Maß der oberen Intervallgrenze für . 1P A 1.2 Die Dreiecke PnBC rotieren um die Gerade BC als Rotationsachse. Zeigen Sie, dass für das Volumen V der dabei entstehenden Rotationskörper in Abhängigkeit von gilt: V() 9 tan ² cm³ . 2P A 1.3 Das Volumen eines Rotationskörpers aus A 1.2 beträgt 6 cm3 . Berechnen Sie das zugehörige Maß . 2P Aufgabe A 2 Haupttermin A 2.0 Ein Leichtathletikverband hat für die Wettbewerbe beim Zehnkampf Funktionsgleichungen festgelegt, mit denen sich die jeweilige Anzahl der Punkte, die die Sportler in den einzelnen Disziplinen erreichen können, berechnen lässt. Beim Weitsprung der Frauen wird die Anzahl der Punkte in Abhängigkeit von der Sprungweite x cm 1,41 I IR 0 IR 0 ) durch die Funktion f1 mit der Gleichung y 0,188807 x 210 ( G ermittelt. Der auf Ganze gerundete Wert für y ergibt die Anzahl der erreichten Punkte. A 2.1 Geben Sie die Definitionsmenge der Funktion f1 an. Zeichnen Sie sodann den Graphen zu f1 in das Koordinatensystem ein. Der bereits eingezeichnete Graph gehört zu der Funktion f2, mit deren Hilfe die Punkte beim Weitsprung der Männer ermittelt werden. y Graph zu f 2 1 200 1 100 1 000 900 800 700 600 500 400 300 200 100 O 100 200 300 400 500 600 700 800 x 3P Seite - 2 - Aufgabe A 2 Haupttermin A 2.2 Ein Mann und eine Frau erreichen beim Weitsprung jeweils 700 Punkte. Ermitteln Sie mit Hilfe der Graphen, um wie viel weiter der Mann dabei gesprungen ist. 1P A 2.3 Eine Frau erreicht beim Weitsprung 900 Punkte. Berechnen Sie die zugehörige Sprungweite auf Zentimeter gerundet. 2P A 2.4 Beim Stabhochsprung der Frauen wird die Anzahl der Punkte in Abhängigkeit von der übersprungenen Höhe x cm durch die Funktion h1 mit der Gleichung 1,35 y 0,44125 x 100 ermittelt, bei den Männern durch die Funktion h2 mit der 1,35 I IR 0 IR 0 . Gleichung y 0, 2797 x 100 G Ein Mann und eine Frau überspringen die gleiche Höhe, dabei erzielt die Frau 500 Punkte mehr als der Mann. Berechnen Sie diese übersprungene Höhe auf Zentimeter gerundet. 3P Seite - 3 - Aufgabe A 3 A 3.0 Haupttermin 1 1 Bn x x auf der Geraden g mit der Gleichung y x 4 4 I IR IR ) bilden für x ]0 ; 7,8[ zusammen mit den Punkten A 0 | 0 , (G Punkte C 4,5 | 3 und D n Drachenvierecke ABn CD n mit der Symmetrieachse AC. A 3.1 Zeichnen Sie die Gerade g, die Symmetrieachse AC sowie das Drachenviereck AB1CD1 für x = 2 und das Drachenviereck AB2CD 2 für x = 4 in das Koordinatensystem ein. y 5 1 O 1 5 x 2P A 3.2 Berechnen Sie die Koordinaten der Punkte D n in Abhängigkeit von der Abszisse x der Punkte Bn . 3P Seite - 4 - Abschlussprüfung 2014 an den Realschulen in Bayern Prüfungsdauer: 150 Minuten Mathematik I Haupttermin Aufgabe B 1 2 cos 3 B 1.0 Der Punkt A 1 2 legt zusammen mit den Pfeilen ABn und 2 5 sin 1 3 cos 3 AD n für [0; 180] Parallelogramme ABn Cn Dn fest. 4 Runden Sie im Folgenden auf zwei Stellen nach dem Komma. B 1.1 Berechnen Sie die Koordinaten der Pfeile AB1 und AD1 für 60 sowie AB2 und AD 2 für 130. Zeichnen Sie sodann die Parallelogramme AB1C1D1 und AB2C2 D 2 in ein Koordinatensystem ein. Für die Zeichnung: Längeneinheit 1 cm; 8 < x < 6 ; 3 < y < 9. 4P B 1.2 Berechnen Sie das Maß des Winkels B1AD1 . 2P B 1.3 Unter den Parallelogrammen ABn Cn D n gibt es das Rechteck AB3C3D3 . Ermitteln Sie rechnerisch das zugehörige Winkelmaß . 4P B 1.4 Zeigen Sie rechnerisch, dass der Trägergraph p der Punkte Cn die Gleichung y 0, 2 x 1 8 2 GI IR IR hat. Zeichnen Sie sodann den Trägergraphen p in das Koordinatensystem zu B 1.1 ein. Teilergebnis : Cn 5 cos 5 sin 2 4P B 1.5 Beim Parallelogramm AB4C4 D 4 liegt der Punkt D4 auf dem Trägergraphen p der Punkte Cn . Bestimmen Sie durch Rechnung das zugehörige Winkelmaß . Bitte wenden! 3P Abschlussprüfung 2014 Prüfungsdauer: 150 Minuten an den Realschulen in Bayern Mathematik I Haupttermin Aufgabe B 2 B 2.0 Das Drachenviereck ABCD mit der Symmetrieachse AC ist die Grundfläche der Pyramide ABCDS, deren Spitze S senkrecht über dem Diagonalenschnittpunkt M der Grundfläche ABCD liegt. Es gilt: AC 9,5 cm ; AM 3,5 cm ; BD 8 cm und SCA 60 . Runden Sie im Folgenden auf zwei Stellen nach dem Komma. B 2.1 Zeichnen Sie das Schrägbild der Pyramide ABCDS, wobei die Diagonale [AC] auf der Schrägbildachse und A links von C liegen soll. Für die Zeichnung gilt: q = 0,5 ; ω = 45°. Berechnen Sie sodann die Längen der Strecken [SM] und [SC] sowie das Maß des Winkels ASC. [Ergebnisse: SM = 10,39 cm; SC = 12 cm; ASC = 48,62° ] 4P B 2.2 Auf der Kante [CS] liegt der Punkt G mit CG 4 cm , auf der Kante [AS] liegen Punkte En . Die Winkel E n GC haben das Maß mit [95,21;180[ . Die Punkte En und der Punkt G sind zusammen mit Punkten Fn [BS] und H n [DS] die Eckpunkte von Drachenvierecken E n Fn GH n mit den Diagonalenschnittpunkten M n . Die Diagonalen [Fn H n ] liegen parallel zu [BD] . Zeichnen Sie den Punkt M1 sowie das Drachenviereck E1FGH 1 1 für 130 in die Zeichnung zu B 2.1 ein. 1P B 2.3 Zeigen Sie durch Rechnung, dass sich die Länge der Strecken [E n G] in Abhängigkeit von φ wie folgt darstellen lässt: 6,00 EnG cm . sin 48,62 Geben Sie die minimale Länge E 0G und das zugehörige Winkelmaß an. 4P B 2.4 Bestimmen Sie die Länge der Strecken [Fn H n ] in Abhängigkeit von . 6,16 sin cm Ergebnis : Fn H n sin 30 B 2.5 Die Drachenvierecke E n Fn GH n bilden die Grundflächen von Pyramiden E n Fn GH nS 4P mit der Spitze S. Punkte Tn E n G sind die Fußpunkte der Höhen [TnS] der Pyramiden E n Fn GH nS . in die Zeichnung zu B 2.1 ein und berechnen Sie das Zeichnen Sie die Höhe [TS] 1 Volumen der Pyramide E1FGH 1 1S . Bitte wenden! 4P