Lösungen zu Blatt 9 Physik 2 im FS 2012

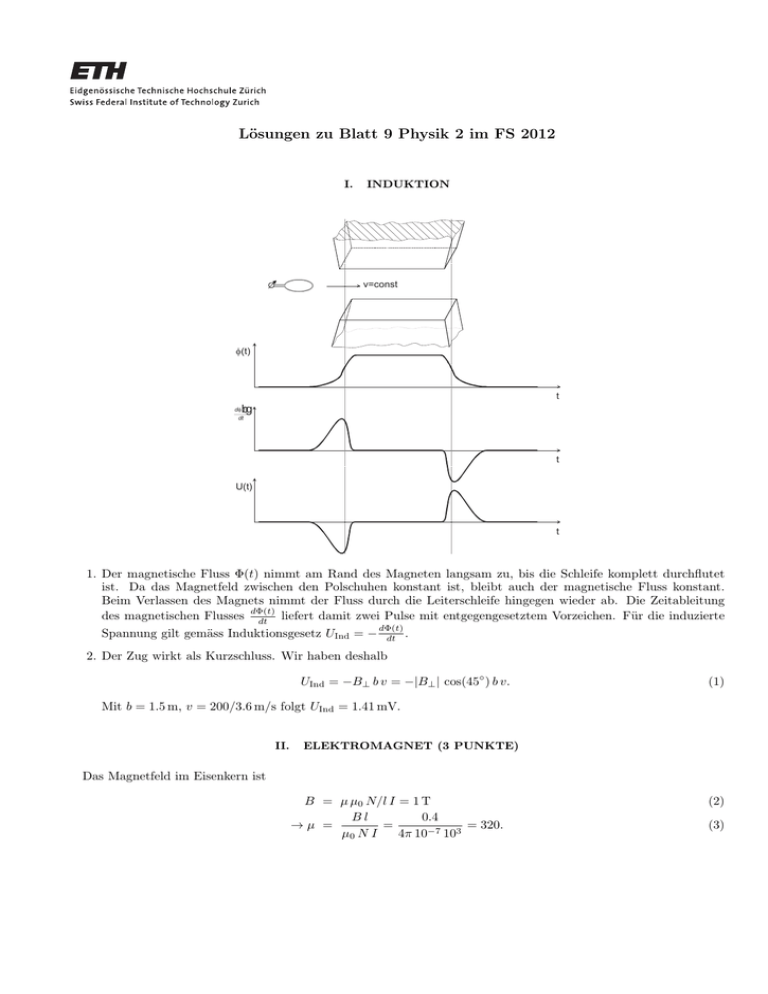
Lösungen zu Blatt 9 Physik 2 im FS 2012
I.
INDUKTION
v=const
f(t)
t
bg
df t
dt
t
U(t)
t
1. Der magnetische Fluss Φ(t) nimmt am Rand des Magneten langsam zu, bis die Schleife komplett durchflutet
ist. Da das Magnetfeld zwischen den Polschuhen konstant ist, bleibt auch der magnetische Fluss konstant.
Beim Verlassen des Magnets nimmt der Fluss durch die Leiterschleife hingegen wieder ab. Die Zeitableitung
des magnetischen Flusses dΦ(t)
liefert damit zwei Pulse mit entgegengesetztem Vorzeichen. Für die induzierte
dt
Spannung gilt gemäss Induktionsgesetz UInd = − dΦ(t)
dt .
2. Der Zug wirkt als Kurzschluss. Wir haben deshalb
UInd = −B⊥ b v = −|B⊥ | cos(45◦ ) b v.
(1)
Mit b = 1.5 m, v = 200/3.6 m/s folgt UInd = 1.41 mV.
II.
ELEKTROMAGNET (3 PUNKTE)
Das Magnetfeld im Eisenkern ist
B = µ µ0 N/l I = 1 T
Bl
0.4
→µ =
=
= 320.
µ0 N I
4π 10−7 103
(2)
(3)
2
Die Induktivität ist
L = µ µ0 (N/l)2 A l = 10 H.
Der Strom ändert sich um 1Ampere pro Millisekunde, d.h.
UInd = −L
dI
dt
= 103 A/s. Die induzierte Spannung ist somit
dI
= −10 Vs A−1 103 A s−1 = −10 · 103 V.
dt
I2
(4)
(5)
I0/e
I1 I1(t<0)
Im Anschluss möchten wir nochmals die Induktionsspannung beim Abschalten einer Stromquelle im generellen
diskutieren, um die Aufgabenstellung zu verdeutlichen. Im Anfangszustand sei in der obrigen Abbildung der Schalter
S geschlossen. Dann fliesst durch den Widerstand R0 der Strom I1 (t < 0) = U0 /R0 , durch die Spule der Strom
I2 (t < 0) = u0 /RL . Für R0 > RL ist I1 < I2 . Wird nun zur Zeit t = 0 der vorher geschlossene Schalter S geöffnet,
so ergibt sich mit den Anfangsbedingungen U0 (t = 0) = 0 und I2 = I0 die Gleichung
0 = I2 R − UInd = I2 R + L
dI2
dt
(6)
mit der Lösung
I2 = I0 e−(R/L) t
(7)
mit R = R0 + RL . Hierbei ist der Widerstand R0 ein Lastwiderstand, während RL der ohmsche Widerstand der Spule
ist. Beim Öffnen des Schalters sinkt der Strom I2 nicht plötzlich auf Null, sondern exponentiell mit der Zeitkonstanten
τ = L/R. Ueber die Spule entsteht eine Induktionsspannung
UInd = −I2 (RL + R0 ) = −L
dI2
dt
(8)
und durch das Messinstrument in fliesst ein grösserer Strom I1 = −I2 in umgekehrter Richtung als vor dem Oeffnen
des Schalters S. Wegen U0 = I0 Rl ergibt sich
UInd = −U0
RL + R0 −(R/L) t
e
,
RL
(9)
so dass für R0 ≫ RL die induzierte Spannung UInd (t = 0) ≈ (R0 /RL ) U0 wesentlich grösser wird als U0 .Deshalb
wird auch der Strom I = UInd /R0 durch R0 viel grösser als vor dem Oeffnen des Schalters. Wird R0 z.B. durch eine
Glühlampe G (siehe Abb.) realisiert, so blitzt diese beim Oeffnen des Schalters hell auf und kann bei sehr grosser
Induktionsspannung sogar durchbrennen.
3
III.
RC-SCHALTKREIS
Der Widerstand und der Kondensator müssen parallel geschaltet sein, sonst würde man keinen endlichen Widerstand
beim Anlegen einer Gleichspannung messen. Der Widerstand des Resistors ist unabhängig ob man eine Gleich- oder
Wechselspannung anlegt (XR = R), der kapazitive Widerstand des Kondensators ist Xc = i ω1 C . Der Gesamtwiderstand in der komplexen Schreibweise lautet dann
XR · XC
R
(
=
XR + XC
iωC R +
R
=
1 + iωRC
R
|X| = √
.
1 + (ω R C)2
X =
1
iωC
)
(10)
(11)
Bei Gleichspannung ist die Frequenz null und der Gesamtwiderstand, |X(ω = 0)| = 100 Ω, vereinfacht sich zu |X(ω =
0)| = R. Somit ist R = 100 Ω. Bei Wechselspannung (ωw = 2π · 50/s) haben wir |X(ωW )| = 20 Ω. Unter Verwendung
der oben hergeleiteten Gleichung können wir nun auch C ausrechnen.
|X(ωW )| = √
100
1 + (2π · 50 · 100)2 C 2
→ C = 156 µF.
(12)
(13)