komplexe zahlen - Meschenmoser.ch
Werbung

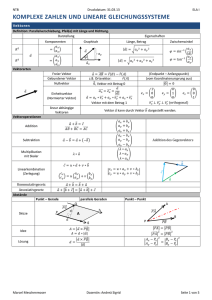
NTB Druckdatum: 31.03.13 ELA I KOMPLEXE ZAHLEN Algebraische oder kartesische Form Imaginärteil Definition Zeiger Betrag Gleichheit Menge der komplexen Zahlen: wenn: Komplexe Zahl j Realteil Polarformen Betrag Trigonometrische Form Exponentialform Argument Eulersche Form Winkel Periodizität y Taschenrechner gibt x NTB will komplex konjugiert Potenzen kartesische Form Exponentialform Rechenoperationen Kartesische Form Addition /Subtraktion Polarform Kommutativgesetz: Assoziativgesetz: Multiplikation Kommutativgesetz: Assoziativgesetz: Distributivgesetz: Division Potenzieren - Radizieren - Jede komplexe Zahl hat n versch. n-te Wurzeln Fundamentalsatz Gleichung 2ten-Grades In gilt: Lösungen: maximal Höhe des Grades Hat man nur reelle Koeffizienten und ist eine Lösung, dann ist Marcel Meschenmoser In gilt: Eine Gleichung n-ten Grades hat genau n Lösungen auch eine Lösung Dozentin: Andreä Sigrid komplexe Lösungen existieren paarweise Seite 1 von 1