komplexe zahlen und lineare gleichungssysteme
Werbung
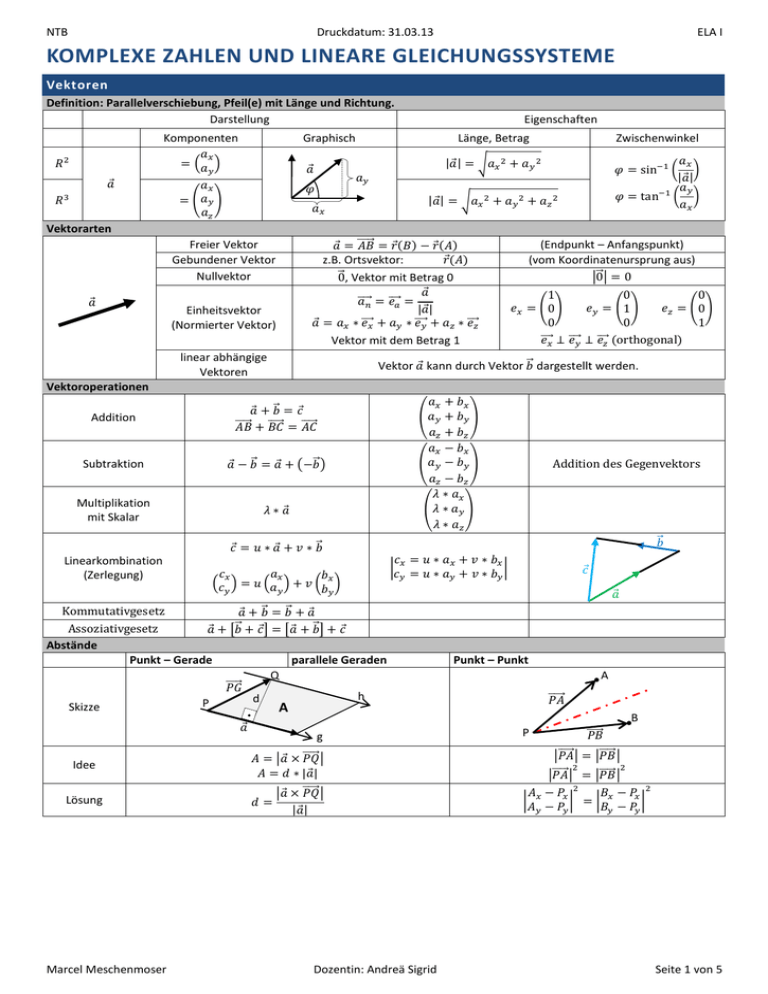
NTB Druckdatum: 31.03.13 ELA I KOMPLEXE ZAHLEN UND LINEARE GLEICHUNGSSYSTEME Vektoren Definition: Parallelverschiebung, Pfeil(e) mit Länge und Richtung. Darstellung Komponenten Eigenschaften Graphisch Länge, Betrag Zwischenwinkel Vektorarten Freier Vektor Gebundener Vektor Nullvektor (Endpunkt – Anfangspunkt) (vom Koordinatenursprung aus) z.B. Ortsvektor: , Vektor mit Betrag 0 Einheitsvektor (Normierter Vektor) Vektor mit dem Betrag 1 linear abhängige Vektoren Vektor kann durch Vektor dargestellt werden. Vektoroperationen Addition Addition des Gegenvektors Subtraktion Multiplikation mit Skalar Linearkombination (Zerlegung) Kommutativgesetz Assoziativgesetz Abstände Punkt – Gerade parallele Geraden Punkt – Punkt Q Skizze P d A h A B g P Idee Lösung Marcel Meschenmoser Dozentin: Andreä Sigrid Seite 1 von 5 NTB Druckdatum: 31.03.13 Skalarprodukt (Multiplikation) Definition Produkt aus der Projektion von auf mit Hilfe des mit dem Betrag des Vektors ELA I Vektorprodukt (Vektorsumme) Operation, die aus 2 Vektoren ein 3ter macht, der zu den Anderen steht (Drehachse). algebraisch Komponente von Drehmoment in geometrisch Null Prüfung nach rechtwinklig (orthogonal) nach kollinear (parallel und antiparallel) Komponenten Antikommutativgesetz Kommutativgesetz Gesetze Distributivgesetz Distributivgesetz Assoziativgesetz Assoziativgesetz Quadrat Verhältnis Wertetabelle 0 1 0 Marcel Meschenmoser 0 0 Dozentin: Andreä Sigrid Seite 2 von 5 NTB Druckdatum: 31.03.13 ELA I Lineare Gleichungssysteme LGlS Definition Beispiel Mehrere Gleichungen (m) mit mehrere Unbekannten (n) nur in der ersten Potenz. 2x2-Gleichungssystem 3x3 Gleichungssystem Lösungsmethoden Einsetzungsverfahren y einsetzen eine nach y auflösen Gleichsetzungsverfahren beide gleichsetzen beide nach y auflösen Additionsverfahren Subtraktionsverfahren beide addieren, subtrahieren eine multiplizieren Multiplikationsverfahren Divisionsverfahren Obere Gauss Algorithmus (mit Faktor mul/div) (zueinander add/sub) (vertauschen) Untere Gauss-Tableau erstellen in Diagonalform bringen in Dreiecksform bringen Anzahl Lösungen inhomogenes LGlS keine Lösungen eine Lösung Lösungen homogenes LGlS y triviale Lösung (immer) Reduzierte Zeilen-Staffel-Form „rre-Form“ 1. Variablen für x g=h y x bis wählen: 2. bekannte Variablen: Gleichung aufstellen 3. Lösungsvektor aufstellen Matrixschreibweise (Schlusskontrolle) Marcel Meschenmoser Dozentin: Andreä Sigrid Seite 3 von 5 NTB Druckdatum: 31.03.13 ELA I Harmonische Schwingung (Trigonometrie) Sinus Cosinus Tangens algebraisch geometrisch y-Koordinate des Punktes P auf dem Einheitskreis x-Koordinate des Punktes P auf dem Einheitskreis y-Koordinate des Punktes H auf dem Tangententräger Kosinussatz Trigonometrischer Pythagoras Definitionsbereich Wertebereich Symmetrie Ersetzung ist abhängig vom Winkel Vorzeichen Ersetzung durch sin Ersetzung durch cos Ersetzung durch tan Sinussatz Gesetze Additionstheoreme Papula S.9497 Zusammenhänge Wertetabelle (mit Hilfe der speziellen Dreiecke) Flächeninhalt Bogenmass Bogenlänge Kreissektor C p A q B Schwingungen differenzieren und integrieren Differenzieren Marcel Meschenmoser Stammfunktion Integrieren Dozentin: Andreä Sigrid Ableitung Differenzieren Integrieren Seite 4 von 5 NTB Druckdatum: 31.03.13 ELA I Komplexe Zahlen Algebraische oder kartesische Form Imaginärteil Definition Zeiger Betrag Gleichheit Menge der komplexen Zahlen: wenn: Komplexe Zahl j Realteil Polarformen Betrag Trigonometrische Form Exponentialform Argument Eulersche Form Winkel Periodizität y Taschenrechner gibt x NTB will komplex konjugiert Potenzen kartesische Form Exponentialform Rechenoperationen Kartesische Form Addition /Subtraktion Polarform Kommutativgesetz: Assoziativgesetz: Multiplikation Kommutativgesetz: Assoziativgesetz: Distributivgesetz: Division Potenzieren - Radizieren - Fundamentalsatz Gleichung 2ten-Grades Jede komplexe Zahl hat n versch. n-te Wurzeln In gilt: Lösungen: maximal Höhe des Grades Hat man nur reelle Koeffizienten und ist eine Lösung, dann ist Marcel Meschenmoser In gilt: Eine Gleichung n-ten Grades hat genau n Lösungen auch eine Lösung Dozentin: Andreä Sigrid komplexe Lösungen existieren paarweise Seite 5 von 5