kathetensatz - mathehotline.de
Werbung

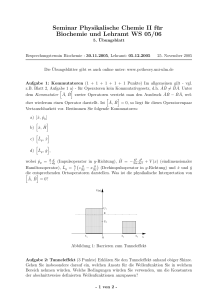
Vektor_b Vektor_a Vektor_p Vektor_c Beweis mithilfe des Skalarprodukts: 2 2 a * c a *( a b ) a a * b a Das Skalarprodukt von a und b ist Null, da a und b orthogonal (senkrecht) zu einander sind (rechtwinkliges Dreieck!). Andererseits ist: a * c a c cos (Winkel zw. a und c) p c p ist die Länge der Projektion von Vektor a auf die Richtung von Vektor c, also Länge von a „mal“ Kosinus des eingeschlossenen Winkels. Aus beiden Überlegungen folgt: 2 a c p