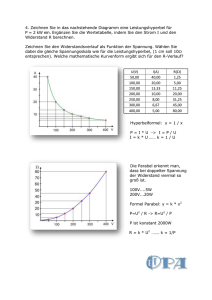
2.2. Quadratische Funktionen 2.2.1. Normalform f(x)

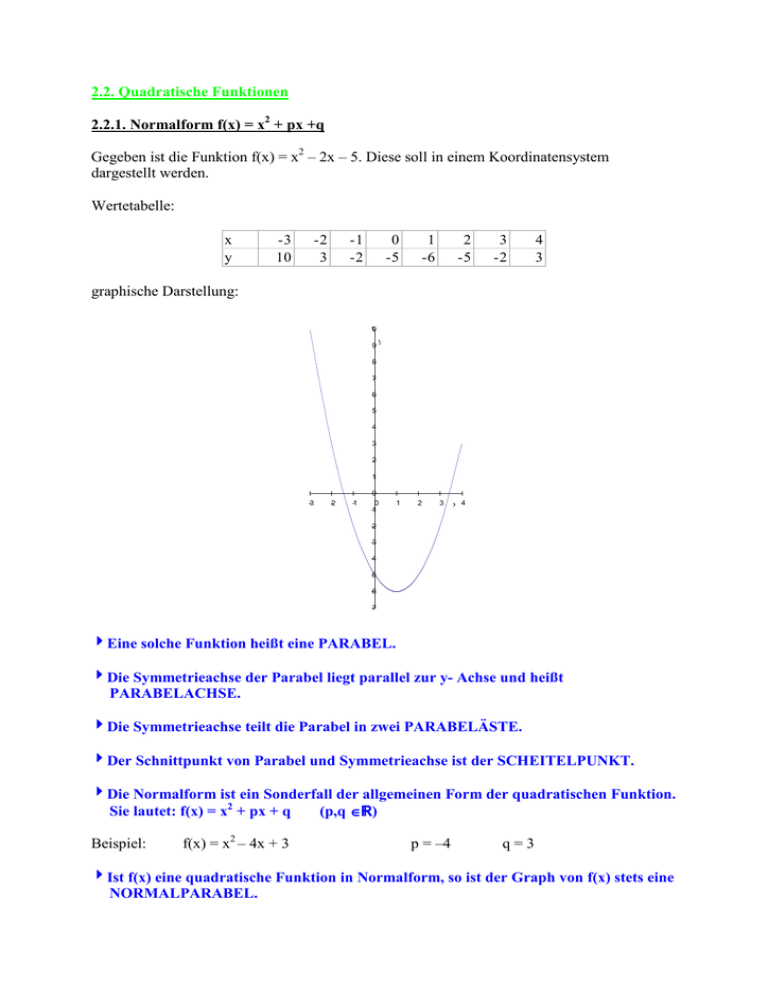
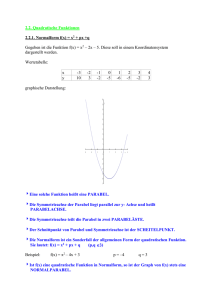
2.2. Quadratische Funktionen
2.2.1. Normalform f(x) = x2 + px +q
Gegeben ist die Funktion f(x) = x2 – 2x – 5. Diese soll in einem Koordinatensystem
dargestellt werden.
Wertetabelle:
x
y
-3
10
-2
3
-1
-2
0
-5
1
-6
2
-5
3
-2
4
3
graphische Darstellung:
10
9
y
8
7
6
5
4
3
2
1
-3
-2
-1
0
0
-1
1
2
3
x 4
-2
-3
-4
-5
-6
-7
4Eine solche Funktion heißt eine PARABEL.
4Die Symmetrieachse der Parabel liegt parallel zur y- Achse und heißt
PARABELACHSE.
4Die Symmetrieachse teilt die Parabel in zwei PARABELÄSTE.
4Der Schnittpunkt von Parabel und Symmetrieachse ist der SCHEITELPUNKT.
4Die Normalform ist ein Sonderfall der allgemeinen Form der quadratischen Funktion.
Sie lautet: f(x) = x2 + px + q
(p,q ∈)
Beispiel:
f(x) = x2 – 4x + 3
p = –4
q=3
4Ist f(x) eine quadratische Funktion in Normalform, so ist der Graph von f(x) stets eine
NORMALPARABEL.