Skalarprodukt, Vektorprodukt, Spatprodukt
Werbung

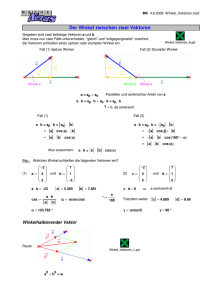
Das Skalarprodukt → − − Das Skalarprodukt zweier Vektoren → a und b mit eingeschlossenem Winkel ϑ ist der Skalar (!) ➞ a θ → − ➞ → − b a • b = a · b · cos ϑ In kartesischen Koordinaten ist das Skalarprodukt zweier Spaltenvektoren bx ax ay • by = ax · bx + ay · by + az · bz bz az → − − −c , Skalar k) Rechenregeln (Vektoren → a , b und → → − → − − → − a • b = b •→ a → − − → → − −c = → − −c + → a + b •→ a •→ b • −c → − − −c • → − −c • → → −c • → − a +→ b a + b =→ → − → − → − − − − (k → a)• b =k → a • b =→ a • k b → − → − − − Wenn → a b (parallel, d.h. Winkel ϑ = 0°)1 , so ist → a • b = a · b. → − → − − − Wenn → a ⊥ b (senkrecht, d.h. Winkel ϑ = 90°), so ist → a • b = 0. → − − Winkel ϑ zwischen zwei Vektoren → a und b → − → − a • b cos ϑ = a·b − Vektor-Komponente von → a in Richtung → −̂ → − → − Länge: a→ a→ − − = a · cos ϑ · b b b → −̂ → −̂ → − = a • b b → − → − a • b → − = b b2 → − von b (orthogonale Projektion) = a · |cos ϑ| → −̂ − = |→ a • b| → − − |→ a • b| = b → − − Beispiel mechanische Arbeit W = F • → s 1 ➞ a θ . ➞ a ➞b → − − (Kraft F , Versatzvektor → s) − → − → → → Wenn − a k b (parallel oder antiparallel, d.h. ϑ = 0° oder ϑ = 180°), so ist − a • b = ±a · b. ➞ b Das Vektorprodukt . ➞ a ➞ b → − − Das Vektorprodukt zweier Vektoren → a und b mit eingeschlossenem Winkel ϑ ist der Vektor (!) → − → − a × b ➞ b θ ➞ a Fläche: a b sin θ definiert durch folgende Eigenschaften: → − → − − − • → a × b steht senkrecht auf → a und b , und zwar so, dass → − → − − − • → a , b und → a × b ein rechtshändiges System bilden. − → − − → − • Der Betrag → a × b ist gleich dem Flächeninhalt des von → a und b aufgespannten Parallelogrammes. In kartesischen Koordinaten ist das Vektorprodukt zweier Spaltenvektoren ay bz − az by bx ax ay × by = az bx − ax bz ax by − ay bx bz az Man beachte die zyklische Vertauschung der Koordinaten: x → y → z → x. → − − −c , Skalar k) Rechenregeln (Vektoren → a , b und → → − → − − → − a × b =−b ×→ a → − − → → − −c = → − −c + → a + b ×→ a ×→ b × −c → − − → −c × → − −c × → − −c × → a + b =→ a +→ b → − → − → − − − − (k → a)× b =k → a × b =→ a × k b → − → − → − − − Wenn → a k b ((anti-)parallel, d.h. Winkel ϑ = 0° oder ϑ = 180°), so ist → a × b = 0. → − − − → − Wenn → a ⊥ b (senkrecht, d.h. Winkel ϑ = 90°), so ist → a × b = a·b (Rechteckfläche). Beispiel Lorentz-Kraft → − → − − F = q→ v ×B − → − → − Beispiel Drehmoment M = → r ×F − (Ladung q, Geschwindigkeitsvektor → v, → − magnetische Induktion oder Flussdichte B ) → − − („Kraftarm” → r , Kraft F ) Das Spatprodukt ➞ ➞ b c ➞ a ➞ c ➞ b a a a → x y z − → − −c = b b b a • b ×→ x y z cx cy cz → − − − von → a, b, → c aufgespanntes orientiertes Volumen (falls rechtshändig: positiv – falls linkshändig: negativ) → − − → − Die Vektoren → a , b und c sindkomplanar (d.h. sie liegen in einer gemeinsamen Ebene), → − − − genau dann wenn → a • b ×→ c = 0 ist.