Geometrie am Oktaeder - von H.

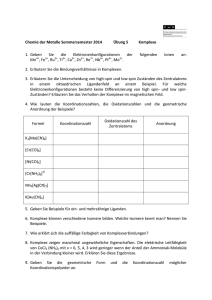
Mathematik-Klausur 13.2 Lf GK6M7
12.11.07
1. Geometrie am Oktaeder
In einem kartesischen Koordinatensystem sind die Punkte A 4∣0∣0 , B1∣4∣0 , C −3∣1∣0
und gegeben.
a) Zeigen Sie durch Rechnung, dass das Dreieck ABC gleichschenklig ist und daß bei B ein
rechter Winkel vorliegt.
b) Bestimmen Sie rechnerisch die Koordinaten des Punktes D so, daß das Viereck ABCD ein
Quadrat ist.
c) Ergänzen Sie rechnerisch die quadratische „Grundfläche“ durch 4
weitere Punkte E, F, G und H so, dass ein Würfel entsteht, der die
Höhe 5 hat.
(Die Zeichnung rechts dient als Orientierungshilfe zur Benennung der Eckpunkte)
d) Fertigen Sie eine Zeichnung des Würfels an.
In dem Würfel wird ein neuer Körper (Oktaeder) dadurch erzeugt, dass die Flächenmittelpunkte des Würfels miteinander verbunden werden. P1 ist der Mittelpunkt der Grundfläche, P2 der Mittelpunkt von ABFE und P5 der Mittelpunkt von AEHD.
e) Berechnen Sie die 3 neuen Punkte und ergänzen Sie den (gesamten) neuen Körper in Ihrer vorhandenen Zeichnung.
Mögliches Zwischenergebnis: P 2 2,5∣2∣2,5 , P 5 2∣−1,5∣2,5
f)
Geben Sie eine Gleichung der Ebene E durch die Punkte P1, P2 und P5 in Parameterform
an.
g) Bestimmen Sie mit einer im Unterricht vorgestellten Methode eine Ebenengleichung
durch P1, P2 und P5 in Koordinatenform.
h) Berechnen Sie den Winkel zwischen zwei benachbarten Kanten des neuen Körpers.
i)
Vom Eckpunkt A des Würfels zum diagonelen Eckpunkt G des Würfels verläuft ein
Draht, der den Oktaeder durchstößt. Berechnen Sie diesen Durchstoßpunkt.
j)
Dem Oktaeder sei eine Kugel einbeschrieben. In welchem Punkt Q berührt die Kugel die
Seitenfläche P1P2P5? Bestimmen Sie auch den Radius dieser Kugel.
Bitte wenden
Mathematik-Klausur 13.2 Lf GK6M7
12.11.07
2. Achsenabschnitte
Zur Vermeidung von Verschmutzungen wurden vor einiger Zeit am Kölner Dom gleichschenklige dreieckige Schutzbleche in den rechtwinklig zueinander angeordneten Säulen-Nischen angebracht. Die folgende Aufgabe bezieht sich auf eine Nischenecke auf dem Boden als
Koordinatenursprung. Die Längenangaben sind in cm. Die Platten-Befestigungspunkte hatten
folgende Koordinaten: A 2,5∣2,5∣100 , B 25∣3∣8 und C 3∣25∣8
a) Geben Sie eine Parameterdarstellung der Blechebene an.
b) Bestimmen Sie aus der Parameterform eine Koordinatenform durch Eliminieren der Parameter.
c) Formen Sie die Koordinatenform in eine Achsenabschnittsform um und bestimmen Sie
mit deren Hilfe die Eckpunkte des Bleches.
d) Eine Taube, die sich entleerte, saß an den Koordinaten D15∣10∣500 . Wo traf sie das
Blech (falls sie traf!)?
e) Berechnen Sie den „Materialverbrauch“ für das Blech (Flächeninhalt ohne Verschnitt).
f)
Berechnen Sie, welchen Abstand das Blech vom Koordinatenursprung hatte?
g) Wie groß war das Volumen, das hinter dem Blech verschwand?
h) Geben Sie (mit Begründung) die Gleichung für ein Seil an, das in E 0∣0∣150 befestigt ist
und nirgends die Blechebene berührt.
Orientierungshilfe zur Punktwertung:
Aufgabe a) b) c) d) e) f) g) h)
i)
j) Summe
1
3 2 2 3 3+2 3 4
4 5+1 5
37
2
2 4 3 3
3
23
3
3 2
Viel Erfolg