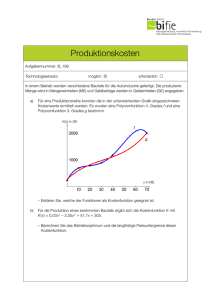
Ein Beispiel zur Kosten- und Preistheorie - Mathe

D1513_F_MO_Beispiel_Kosten_und_Preistheorie_XP.wxmx
1 / 5
Ein Beispiel zur Kosten- und
Preistheorie
Dokumentnummer: D1513
Fachgebiet: Funktionen, Analysis
Einsatz: 4HAK (drittes Lernjahr)
1 Problembeschreibung
Gegeben ist eine quadratische Kostenfunktion. Das Betriebsoptimum und
die langfristige Preisuntergrenze sind gesucht.
Definition: Das Betriebsoptimum ist jene Produktionsmenge, bei der die
Durchschnittskosten ein Minimum annehmen.
2 Problemlösung
EINGABE
(die quadratische Kostenfunktion darf verändert werden */
(%i50) K:K(x):=x**2+8*x+36
/* die quadratische Kostenfunktion */;
2
(%o50) K( x ):= x + 8 x + 36
VERARBEITUNG
Definition: Die Durchschnittskosten erhält man, in dem man die Gesamtkosten
durch die Menge dividiert.
(%i51) DK(x):=K(x)/x;
K( x )
(%o51) DK( x ):=
x
Betriebsoptimum
(%i52) ab:diff(DK(x),x);
2
(%o52)
2 x + 8 x + 8 x + 36
2
x
x
(%i53) l:solve(ab=0,x);
(%o53) [ x = - 6 , x = 6 ]
(%i54) BO:ev(x,l[2]);
(%o54) 6
(%i55) BO:BO,numer;
(%o55) 6
(%i56) BO:floor(BO*100+0.5)/100.0;
(%o56) 6.0
D1513_F_MO_Beispiel_Kosten_und_Preistheorie_XP.wxmx
2 / 5
Definition: Das Minimum der Durchschnittskosten wird als langfristige
Preisuntergrenze bezeichnet.
Dazu muss man das Betriebsoptimum in die Durchschnittskosten
einsetzen.
(%i57) LPU:DK(BO);
(%o57) 20.0
(%i58) LPU:floor(LPU*100+0.5)/100.0;
(%o58) 20.0
EINGABE
Einen brauchbaren Preis erhält man, wenn man die Preisuntergrenze
mit einem Faktor größer als 1 multipliziert (warum?)
(%i59) VF:3
/* Multiplikationsfaktor für die Preisermittlung */;
(%o59) 3
VERARBEITUNG
(%i60) p:LPU*VF;
(%o60) 60.0
Definition: Umsatz (Erlös) = Menge X Preis
(%i61) U(x):=p*x;
(%o61) U( x ):= p x
(%i62) U(x);
(%o62) 60.0 x
Definition: Gewinn = Erlös - Kosten
(%i63) G(x):=U(x)-K(x);
(%o63) G( x ):= U( x )- K( x )
(%i64) G(x);
2
(%o64) - x + 52.0 x - 36
Ermittlung der Gewinnzone:
- die Nutzenschwelle ist die untere Grenze der Gewinnzone
- die Nutzengrenze ist die obere Grenze der Gewinnzone
(%i65) l:solve(G(x)=0,x);
rat: replaced 52.0 by 52/1 = 52.0
(%o65) [ x = 26 - 8 10 , x = 8 10 + 26 ]
(%i66) l:l,numer;
(%o66) [ x = 0.70177871865296 , x = 51.29822128134704 ]
Nutzenschwelle (Break Even Point)
D1513_F_MO_Beispiel_Kosten_und_Preistheorie_XP.wxmx
(%i67) NS:x,l[1];
(%o67) 0.70177871865296
Kaufmännische Rundung
(%i68) NS:floor(NS*10+0.5)/10.0;
(%o68) 0.7
Nutzengrenze
(%i69) NG:x,l[2];
(%o69) 51.29822128134704
Kaufmännische Rundung
(%i70) NG:floor(NG*10+0.5)/10.0;
(%o70) 51.3
Den maximalen Gewinn bestimmen: die notwendige Bedingung
ist das Verschwinden der ersten Ableitung.
(%i71) ab:diff(G(x),x);
(%o71) 52.0 - 2 x
(%i72) l:solve(ab=0,x);
rat: replaced 52.0 by 52/1 = 52.0
(%o72) [ x = 26 ]
Gewinnmaximale Menge: diese wird auch Cournotsche Menge
genannt und muss aus der Listen l herausgefiltert werden.
(%i73) CM:x,l[1];
(%o73) 26
(%i74) CM:CM,numer;
(%o74) 26
Maximaler Gewinn: man muss die gewinnmaximale Menge in
die Gewinnfunktion einsetzen
(%i75) GM:G(CM);
(%o75) 640.0
(%i76) GM:floor(GM*100+0.5)/100.0;
(%o76) 640.0
AUSGABE
(%i77) print("Kostenfunktion",K)$
2
Kostenfunktion K( x ):= x + 8 x + 36
(%i78) print("Betriebsoptimum",BO)$
Betriebsoptimum 6.0
3 / 5
D1513_F_MO_Beispiel_Kosten_und_Preistheorie_XP.wxmx
(%i79) print("langfristige Preisuntergrenze",LPU)$
langfristige Preisuntergrenze 20.0
(%i80) print("Verkaufspreis",p)$
Verkaufspreis 60.0
(%i81) print("Nutzenschwelle",NS)$
Nutzenschwelle 0.7
(%i82) print("Nutzengrenze",NG)$
Nutzengrenze 51.3
(%i83) print("gewinnmaximale Menge",CM)$
gewinnmaximale Menge 26
(%i84) print("maximaler Gewinn",GM)$
maximaler Gewinn 640.0
3 Wo wird das im Unterricht eingesetzt?
Funktionen
Gleichungen
Differential- und Integralrechnung
Kosten- und Preistheorie
(%i85) x;
(%o85) x
4 Protokollierung Aufgabe
4 / 5
D1513_F_MO_Beispiel_Kosten_und_Preistheorie_XP.wxmx
5 / 5
(%i86) print("")$
print("Aufgabenstellung")$
print("----------------")$
print("gegebene quadratische Kostenfunktion ",K)$
print("gegebener Preis
",p)$
print("=========================")$
print("Der Rest ist gesucht, die erwarteten Ergebnisse sind angezeigt")
print("Betriebsoptimum ",BO)$
print("langf. Preis-UG ",LPU)$
print("Nutzenschwelle ",NS)$
print("Nutzengrenze
",NG)$
print("gewinnmax. Menge",CM)$
print("Gewinnmaximum
",GM)$
Aufgabenstellung
---------------2
gegebene quadratische Kostenfunktion K( x ):= x + 8 x + 36
60.0
gegebener Preis
=========================
Der Rest ist gesucht, die erwarteten Ergebnisse sind angezeigt
Betriebsoptimum 6.0
langf. Preis-UG 20.0
Nutzenschwelle 0.7
51.3
Nutzengrenze
gewinnmax. Menge 26
640.0
Gewinnmaximum