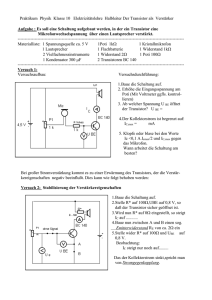
Der Transistor als Verstärker

6
Der Transistor als Verstärker
Bei den Anwendungen von Transistoren als Schalter traten eigentlich nur zwei
Betriebszustände auf: der sperrende und der gesättigte Transistor. Die Schaltungen
waren bewusst so ausgelegt, dass Zwischenstellung nur ganz kurze Zeit während
des Umschaltens auftreten konnten. Im Gegensatz dazu steht bei der Verstärkeranwendung eine proportionale Verarbeitung von Signalen im Vordergrund. Die Ausgangsgrösse eines analogen Systems soll zu einer Eingangsgrösse linear
proportional sein. Man spricht deshalb in diesem Zusammenhang auch häufig kurz
von linearen Schaltungen (linear circuits). Es versteht sich von selbst, dass jetzt
sperrende oder gesättigte Transistoren nicht mehr vorkommen sollten.
6.1
Arbeitspunkteinstellung
Die meisten zu verstärkenden Signale sind Wechselsignale. Die Ströme in einem
Transistor können aber bedingt durch die pn-Übergänge nur immer in einer Richtung fliessen. Damit Wechselsignale überhaupt verarbeitet werden können, muss
man ihnen erst ein Gleichsignal überlagern, dessen Grösse so beschaffen ist, dass
das resultierende Signal das Vorzeichen nicht mehr wechselt. Diese Gleichgrössen
werden auch als Ruhegrössen oder Arbeitspunktgrössen bezeichnet.
2
Der Transistor als Verstärker
Wechselsignal
Ruhegrösse
Überlagerung
Abb. 6.1: Überlagerung von Wechselsignal und Ruhegrösse
Aus naheliegenden Gründen müssen diese Arbeitspunktgrössen stabil sein, das
heisst, dass sie sich nicht ändern dürfen bei Temperaturschwankungen (Temperaturstabilität) und beim Ersatz eines Transistors durch ein anderes Exemplar desselben Typs (Exemplarstreuung). In den folgenden Abschnitten sollen einige
Möglichkeiten der Arbeitspunkteinstellung bei Transistoren vorgestellt und
hinsichtlich ihres Verhaltens bezüglich der Exemplarstreuung und bezüglich der
Temperaturstabilität untersucht werden.
6.1.1
Konstante Basis-Emitter-Spannung
Naheliegend wäre es, die Basis-Emitter-Spannung UBE konstant zu halten und
damit auch einen definierten Kollektorstrom einzustellen. Eine mögliche Schaltung
ist in Abbildung 6.2 gezeigt:
+12V
1.2kΩ
RC
5.6kΩ
IC
100Ω
UBE
Abb. 6.2: Schaltung mit konstantem UBE
Mit dem Potentiometer (zum Beispiel mit einem 10-Gang-Potentiometer) kann ein
genau definierter Wert für UBE eingestellt werden. Damit wird auch ein ebenso
definierter Kollektorstrom IC fliessen, da Kollektorstrom und Basis-Emitter-Spannung über die Diodengleichung miteinander verknüpft sind (Abbildung 6.3).
6.1 Arbeitspunkteinstellung
3
IC
IC
UBE
UBE
Abb. 6.3: IC in Abhängigkeit von UBE
Wenn man diese Schaltung aufbaut und die Ströme und Spannungen misst, so stellt
man fest, dass sich der Kollektorstrom schon stark ändert, wenn das Gehäuse des
Transistors mit den Fingern berührt wird. Der Grund liegt in der enorm starken
Temperaturabhängigkeit der Spannung UBE; es gilt bekanntlich, dass UBE bei konstantem Strom um etwa 2 mV/K mit der Temperatur abnimmt; die Kennlinie verschiebt sich also etwas nach links (Abbildung 6.4):
IC
ICw
warm
ICk
kalt
UBE
UBE
Abb. 6.4: Kennlinien bei verschiedenen Temperaturen
Die relativ geringfügige Verschiebung der Kennlinie bewirkt infolge der grossen
Steilheit der Kennlinien eine massive Verschiebung des Schnittpunktes (= Arbeitspunkt) in Richtung höhere Kollektorströme. Dieser Stromanstieg kann sogar zur
Folge haben, dass der Transistor sättigt, also als Verstärker nicht mehr gebraucht
werden kann.
Die hier vorgeschlagene Schaltung ist offensichtlich thermisch nicht stabil und
kann deshalb in der Praxis nicht verwendet werden. Die in der Literatur teilweise
4
Der Transistor als Verstärker
vorgeschlagenen Lösungen mit temperaturabhängigen Widerständen im Spannungsteiler zur Kompensation des Temperaturverhaltens des Transistors müssen
eher als akademische Spielereien betrachtet werden. Gründe dafür sind einerseits
der Preis für die relativ vielen zusätzlichen Bauelemente und anderseits die Tatsache, dass ein NTC-Widerstand ein anderes Temperaturverhalten hat als ein Transistor und zudem nicht sichergestellt ist, dass Transistor und NTC die gleiche
Temperatur haben.
6.1.2
Konstanter Basisstrom
Nun wollen wir versuchen, die zweite Eingangsgrösse, den Basisstrom, konstant zu
halten. Die Schaltung von Abbildung 6.5 genügt diesem Anspruch, wie die folgende Analyse zeigt.
UCC
RB
RC
IB
IC
UBE
Abb. 6.5: Schaltung für konstanten Basisstrom
Für den Basisstrom erhalten wir durch Anwendung des Maschensatzes:
U CC – U BE
I B = ---------------------------RB
Damit erhält man sofort für den Kollektorstrom:
β ⋅ ( U CC – U BE )
I C = β ⋅ IB = ----------------------------------------RB
Da üblicherweise gilt: UCC >> UBE, bewirkt eine temperaturbedingte Änderung
der Basis-Emitter-Spannung nur eine Veränderung des Basisstromes, die innerhalb
der Messunsicherheit liegt, für uns also unbedeutend ist.
6.1 Arbeitspunkteinstellung
5
12V
1.2MΩ
mA
2N2219A
mV
Abb. 6.6: Mess-Schaltung
Mit der Schaltung von Abbildung 6.6 wollen wir die Temperaturabhängigkeit des
Kollektorstromes IC überprüfen. Zur Temperaturmessung können wir die BasisEmitter-Spannung heranziehen, da UBE ja bekanntlich bei steigender Temperatur
mit 2 mV/K abnimmt. Man erhält bei dieser Messung allerdings keine absolute
Temperatur, sondern nur die Temperaturdifferenz. Dafür sind die Messwerte ein
Mass für die massgebende Kristalltemperatur und nicht nur für die Gehäusetemperatur, die man mit gewöhnlichen Temperatur-Messsonden hätte bestimmen können.
Bei der Durchführung des Experimentes soll der Transistor vorsichtig mit einem
Lötkolben erwärmt werden. Dabei sollen jeweils gleichzeitig (also bei derselben
Temperatur) die Werte für UBE und IC abgelesen werden. Bei dieser Messung stellt
man fest, dass der Kollektorstrom mit steigender Temperatur zunimmt. Da der
Basisstrom aber praktisch konstant bleibt, muss offenbar die Stromverstärkung $
zunehmen. In der folgenden Abbildung 6.7 wurde deshalb das Verhältnis $/$0 über
der Temperatur aufgetragen; $0 ist dabei die Stromverstärkung bei der Ausgangstemperatur.
1.6
β/β0
1.5
1.4
1.3
1.2
1.1
1.0
0
20
40
60
80
100K
∆ϑ
Abb. 6.7: Temperaturabhängigkeit der Stromverstärkung $
6
Der Transistor als Verstärker
Wir erkennen, dass die Stromverstärkung etwa linear mit der Temperatur zunimmt.
Das Mass der Temperaturabhängigkeit ist von Transistor zu Transistor etwas verschieden; wir wollen uns den folgenden Zusammenhang merken:
Die Stromverstärkung $ eines Transistors nimmt mit steigender Temperatur um
maximal 1% pro K zu.
Die thermische Stabilität des Ruhestromes ist also wesentlich besser als bei der
vorhergehenden Schaltung. Hinsichtlich der Stabilität gegenüber der Exemplarstreuung sieht es ungünstiger aus. Der sich einstellende Kollektorstrom IC ist direkt
proportional zur Stromverstärkung $. Bei einem typischen Transistor (2N2219A)
kann $ zwischen 75 und 350 schwanken; der Kollektorstrom kann demzufolge auch
in einem Verhältnis von fast 1:5 schwanken. Aus diesem Grund ist auch diese
Schaltung zur Einstellung eines stabilen Arbeitspunktes nicht geeignet. Bei einer
Serienproduktion der Schaltung wäre für jeden Transistor ein eigens abgeglichener
Basiswiderstand RB notwendig; solche Abgleichprozesse sind aber sehr zeitaufwendig und daher wirtschaftlich nur in Ausnahmefällen vertretbar. Die Schaltung
(Abbildung 6.6) eignet sich aber sehr gut als einfaches Transistor-Testgerät: da der
Basisstrom IB konstant ist, kann das Amperemeter im Kollektorkreis direkt für die
Stromverstärkung $ geeicht werden.
6.1.3
Emitterstrom-Gegenkopplung
Will man in der Technik eine von verschiedenen Parametern abhängige Grösse konstant halten, so kann man sie messen, den gemessenen Istwert mit einem Sollwert
vergleichen und dann je nach Resultat des Vergleichs die Grösse beeinflussen.
Dieser Prozess wird üblicherweise als Regelung bezeichnet, in der Elektronik
spricht man auch von einer sog. Gegenkopplung. Der Begriff “Messen” bedeutet in
der Technik die Umwandlung einer physikalischen Grösse in eine andere, die im
Idealfall linear proportional zur Ausgangsgrösse ist. Die Grundelemente einer
Regelung oder eben Gegenkopplung sind in der Schaltung von Abbildung 6.8
erkennbar. In erster Näherung (Spannungsteiler als unbelastet betrachtet) erhält
man für das Basis-Potential UB:
U CC ⋅ R 2
U B = ---------------------R1 + R 2
Daraus folgt für den Kollektorstrom IC, den wir auch hier wieder dem Emitterstrom
IE etwa gleich setzen:
6.1 Arbeitspunkteinstellung
7
U B – U BE
IC ≈ I E = -----------------------RE
UCC
UB
R1
IC
UBE
IE
R2
RE
UE
Abb. 6.8: Emitterstrom-Gegenkopplung
Der Emitterstrom (und damit auch der Kollektorstrom) wird mit dem Widerstand
RE gemessen (d.h. in eine proportionale Spannung UE umgewandelt) und mit dem
durch den Spannungsteiler eingestellten Sollwert UB verglichen. Das Resultat des
Vergleichs ist die Spannung UBE (Maschensatz: UBE = UB - UE). Sollte der Emitterstrom aus irgendeinem Grund ansteigen, so würde auch die Spannung UE
grösser. Da UB konstant bleibt, muss also UBE kleiner werden, was nach unserem
Wissen eine Verkleinerung des Kollektorstromes zur Folge hat. Man erkennt leicht,
dass jede Änderung des Emitterstromes eine Änderung der Spannung UBE bewirkt,
die der ursprünglichen Änderung des Emitterstromes entgegenwirkt, der Emitterstrom also geregelt wird.
Für eine genauere Analyse der Schaltung können wir den Spannungsteiler durch
eine Ersatzspannungsquelle (Thévenin) darstellen und erhalten dann die folgende
Ersatzschaltung (Abbildung 6.9):
R1||R2 = Rp
IB
UBE
UB0
IE
RE
Abb. 6.9: Ersatzschaltung
8
Der Transistor als Verstärker
Für die eingeprägte Spannung der Spannungsquelle (= Leerlaufspannung des Spannungsteilers) erhält man leicht:
U CC ⋅ R 2
U B0 = ---------------------R1 + R 2
Die Anwendung des Maschensatzes liefert die folgende Gleichung:
U B0 = IB ⋅ R p + U BE + β ⋅ IB ⋅ RE
Diese Beziehung kann nun nach dem Basisstrom IB aufgelöst werden:
U B0 – U BE
IB = --------------------------Rp + β ⋅ R E
Mit IC = $ IB kann man nun den genauen Kollektorstrom berechnen:
U B0 – U BE
I C = --------------------------Rp
R E + -----β
Der sich in dieser Schaltung einstellende Kollektorstrom soll nun genauer bezüglich
der Temperaturabhängigkeit und bezüglich der Abhängigkeit von der Stromverstärkung überprüft werden.
Temperaturstabilität
Die Temperatur hat einerseits einen Einfluss auf die Stromverstärkung $ und anderseits auf die Basis-Emitter-Spannung UBE. Da die Stromverstärkung infolge der
Exemplarstreuung schon grossen Schwankungen unterworfen ist, kann ihre Temperaturabhängigkeit zusammen mit der Exemplarstreuung behandelt werden; in
dieser Untersuchung soll also nur die Temperaturabhängigkeit der Basis-EmitterSpannung betrachtet werden. Um vergleichbare Ergebnisse zu erhalten, wird die
relative Schwankung des Kollektorstromes berechnet:
6.1 Arbeitspunkteinstellung
I Cmax – ICmin
∆I C
c ⋅ ∆ϑ
--------- = ---------------------------------- = --------------------------IC
I Cmin
U B0 – U BE
9
mV
c = 2 -------K
Die im Nenner auftretende Differenz UB0 - UBE ist nichts anderes als das EmitterRuhepotential UE; damit kann die Beziehung noch einfacher geschrieben werden:
∆I C
c ⋅ ∆ϑ
--------- = -------------IC
UE
Die temperaturbedingte Schwankung des Kollektorstromes wird umso kleiner, je
grösser das Emitter-Ruhepotential UE gewählt wird.
Exemplarstreuung
Es zeigt sich, dass die Rechnung stark vereinfacht wird, wenn man annimmt, dass
die Stromverstärkung $ zwischen einem Minimalwert und unendlich schwankt.
β min ≤ β ≤ ∞
Nach einigen einfachen Zwischenrechnungen erhält man für die relative Kollektorstrom-Änderung:
Rp
∆I C
--------- = ---------------------IC
β min ⋅ R E
Die Kollektorstromschwankung wird umso kleiner, je kleiner der Widerstand Rp
(= R15R2) gewählt wird.
Zahlenbeispiel
Gegeben seien die folgenden Werte: UCC = 12 V, IC = 2 mA, UBE . 0.6 V,
)h = 50°C, $min = 100.
Temperaturschwankung und Exemplarstreuung sollen je für sich einen relativen
Stromfehler von maximal 10% verursachen. Gesucht sind die Widerstandswerte für
R1, R2 und RE.
10
Der Transistor als Verstärker
c ⋅ ∆ϑ
0.002 ⋅ 50
U E ≥ -------------- = ------------------------ V = 1V
∆I C
0.1
--------IC
UE
1V
R E = ------- = ----------- = 500Ω
IC
2mA
→
∆I C
R p ≤ --------- ⋅ β min ⋅ R E = 0.1 ⋅ 100 ⋅ 500Ω = 5kΩ
IC
Aus den beiden Gleichungen
R1 ⋅ R 2
-----------------Rp =
R1 + R2
und
U CC ⋅ R 2
--------------------U B0 =
R1 + R2
mit
U B0 = U E + U BE
folgt leicht:
R1
Rp
--------- = ---------- →
U B0
U CC
U CC
R 1 = R p ⋅ ----------- = 37.5kΩ →
U B0
1
R2 = ------------------- = 5.77kΩ
1
1- --------– Rp R1
Die auf diese Weise gefundenen Widerstandswerte müssen auf Normwerte (üblicherweise aus den Normreihen E12 oder E24) gerundet werden. Unter Verwendung
der Reihe E12 erhält man:
RE = 470 S, R1 = 33 kS, R2 = 5.6 kS
Mit den gerundeten Werten sollte nochmals eine Kontrollrechnung durchgeführt
werden, um sicherzustellen, dass die ursprünglichen Vorgaben eingehalten worden
sind. Resultat der Kontrollrechnung:
U CC ⋅ R 2
U B0 = ---------------------- = 1.74V
R1 + R2
→
U E = 1.14V
R p = R 1 || R 2 = 4.788kΩ ≤ 0.1 ⋅ β min ⋅ R E = 4.7kΩ
Die zweite Bedingung ist nicht mehr erfüllt. Eine kurze Analyse zeigt, dass mit den
gewählten Werten der Kollektorstrom zu gross wird (nämlich mehr als 2.4 mA).
Das lässt sich korrigieren, indem für RE ein Wert von 560 S gewählt wird. Dadurch
sinkt der Kollektorstrom auf die geforderten 2 mA ab und die zweite Ungleichung
6.1 Arbeitspunkteinstellung
11
ist nun auch erfüllt. Wie man bei diesem Beispiel sieht, sollte nie auf die Kontrollrechnung verzichtet werden; meist genügen geringfügige Änderungen bei den Rundungen, um die gewünschten Werte zu erhalten.
Diese Art der Dimensionierung ist offenbar recht aufwendig und wird deshalb in
der Praxis nur dann angewendet, wenn an die Stabilität eines Arbeitspunktes sehr
hohe Anforderungen gestellt werden. In den meisten Fällen arbeitet man mit einer
Faustregel, die ein einfaches und schnelles Dimensionieren ermöglicht.
Faustregel für die Arbeitspunkt-Einstellung
! Das Emitter-Ruhepotential UE sollte etwa 1 ... 3 V betragen, was eine genügende thermische Stabilität garantiert.
!
Der Querstrom IQ = UCC/(R1+R2) durch den Basisspannungsteiler sollte
mindestens 10 mal grösser sein, als der maximal erwartete Basisstrom
IBmax = IC/$min.
Unter Beachtung dieser Faustregel lassen sich Schaltungen mit wenig Aufwand
durch blosse Anwendung des Ohmschen Gesetzes dimensionieren. Selbstverständlich muss auch in diesem Fall nach der Rundung auf Normwerte nochmals
eine Kontroll-Rechnung durchgeführt und gegebenenfalls die Rundung etwas angepasst werden.
Neben der eben behandelten Emitterstrom-Gegenkopplung gibt es noch andere
Gegenkopplungsverfahren wie zum Beispiel die Spannungsgegenkopplung. Diese
Schaltungen sind aber aufwendiger zu dimensionieren und die Stabilität des
Arbeitspunktes ist etwas schlechter. Sie werden deshalb nur in bestimmten Fällen
eingesetzt und dienen hier nur als Übungsaufgaben.
Allgemein ist zur Arbeitspunkteinstellung und zur Stabilität zu sagen, dass man nie
Schaltungen entwerfen sollte, bei denen das richtige Funktionieren von einer
genauen Einhaltung der Arbeitspunktgrössen abhängig ist. Wenn man an die Grenzen geht, ist damit zu rechnen, dass relativ viel Ausschuss produziert wird.
12
Der Transistor als Verstärker
6.2
Einfache Verstärkerschaltung
UCC
R1
RC
R2
RE
C
u1
u2
Abb. 6.10: Verstärkerschaltung
Durch Ergänzung der Schaltung zur Arbeitspunkteinstellung durch einen Kollektorwiderstand und kapazitive Einkopplung (Überlagerung) des Signals an die
Basis erhält man die obenstehende Verstärkerschaltung (Abbildung 6.10). Zur
Berechnung der Verstärkung kann man als Eingangssignal u1 einen Spannungssprung der Grösse )U1 annehmen. Da sich die Spannung an einem Kondensator
nicht sprunghaft ändern kann, überträgt sich dieser Sprung direkt an die Basis des
Transistors. Unter der früher gemachten Voraussetzung einer konstanten BasisEmitter-Spannung steigt demzufolge die Spannung über dem Emitterwiderstand RE
auch um )U1 an. Demzufolge muss der Emitterstrom um )U1/RE anwachsen. Da
der Kollektorstrom etwa gleich dem Emitterstrom ist, muss auch der Kollektorstrom um diesen Betrag anwachsen. Als Folge davon wächst der Spannungsabfall
am Kollektorwiderstand RC um )U1 · (RC/RE). Das bedeutet, dass die Ausgangsspannung u2 um eben diesen Betrag abnehmen muss, da ja die Spannung über RC
und die Ausgangsspannung zusammen die konstante Betriebsspannung UCC ergeben müssen. Aufgrund dieser Überlegungen erhält man für die Spannungsverstärkung dieser Schaltung den folgenden Ausdruck:
u2
RC
----vu =
= – ------u1
RE
Die folgende Schaltung (Abbildung 6.11) wurde gemäss der Faustregel dimensioniert, wobei eine Ruhespannung UE von etwa 1.5 V gewählt wurde. Nach der Rundung auf Normwerte ergibt sich noch eine Spannung von 1.2 V. Als Testsignal wird
eine Dreieck-Spannung verwendet, da dabei allfällige Verzerrungen von blossem
Auge viel besser wahrgenommen werden können als bei Verwendung eines SinusSignals.
6.2 Einfache Verstärkerschaltung
13
+12V
100kΩ
u1
3.3kΩ
1µ F
2N2219A
18kΩ
1.5kΩ
u2
Abb. 6.11: Test-Schaltung
Die Messresultate sind in Abbildung 6.12 dargestellt, wobei auf dem KO-Bild nur
die Wechselsignal-Anteile dargestellt sind (Messung in Stellung AC).
u1(t)
u2(t)
2V
12V
1V
10V
0V
8V
-1V
6V
-2V
4V
-3V
2V
-4V
0V
-5V
-2V
-6V
-4V
20µs/DIV
Abb. 6.12: Ein- und Ausgangsspannung der Test-Schaltung
Man erkennt sehr schön, dass das Minuszeichen bei der Verstärkung nichts anderes
bedeutet, als eine Phasendrehung des Signals um 180°. Man spricht dann auch etwa
von Inversion bzw. von einem invertierenden Verstärker. Die Verstärkung entspricht
ziemlich genau dem theoretisch erwarteten Wert von ca. -2.2 (= -RC/RE). Wenn bei
dieser Messung die Amplitude der Eingangsspannung immer weiter vergrössert
wird, so zeigen sich verschiedene Verzerrungen beim Ausgangssignal. Den Ursachen dieser Verzerrungen kommt man am ehesten auf die Spur, wenn - wie in
14
Der Transistor als Verstärker
Abbildung 6.13 gezeigt - das Kollektor- und das Emitterpotential oszillografiert
werden.
+12V
100kΩ
1µF
u1
18kΩ
3.3kΩ
2N2219A
1.5kΩ
UE
UC
Abb. 6.13: Mess-Schaltung
Gemäss den vorherigen Überlegungen ist ja die Emitterspannungsänderung gleich
der Basisspannungsänderung, also gleich dem Eingangssignal. In Abbildung 6.14
sind diese beiden Potentiale dargestellt und zwar für eine sehr große Amplitude der
Eingangsspannung. Für beide Signale wurde DC-Kopplung, gleiche Lage des
Masse-Potentials und der gleiche Ablenkfaktor gewählt.
UE(t)
UC(t)
14V
14V
12V
12V
10V
10V
8V
8V
6V
6V
4V
4V
2V
2V
0V
0V
-2V
-2V
20µs/DIV
Abb. 6.14: Emitter- und Kollektorpotential beim übersteuerten Verstärker
Die Reihenfolge des Auftretens der im folgenden beschriebenen Effekte hängt von
der Wahl des Arbeitspunktes ab. Bei der im Beispiel verwendeten Wahl tritt bei der
Vergrösserung der Signalamplitude zuerst der Fall ein, dass das Eingangssignal
6.2 Einfache Verstärkerschaltung
15
gleich der Emitter-Ruhespannung wird. Damit wird die momentane Emitterspannung gleich Null; es fliesst also kein Strom mehr durch den Transistor, der Transistor sperrt und das Kollektorpotential ist gleich der Betriebsspannung (im Bild z.B.
etwa zwischen 40 und 100 µs). Bei positiver Eingangsspannung steigt das Emitterpotential und damit auch der Emitterstrom (=Kollektorstrom) an, das Kollektorpotential sinkt entsprechend. Bei einer weiteren Vergrösserung der Signalamplitude
wird die Kollektor-Emitterspannung UCE gleich Null. Eine weitere Steigerung führt
zur Sättigung des Transistors (im Bild z.B. bei etwa 10 bis 30 µs). Man erkennt im
Bild sehr deutlich, dass im Falle der Sättigung die Kollektor-Basis-Diode des Transistors in Flussrichtung betrieben wird und demnach die Ausgangsspannung sich
gleichphasig mit der Eingangsspannung ändert. Auffällig ist die negative Spitze des
Emitterpotentials bei ca. 70 µs. Hier muss offenbar ein negativer Emitterstrom
fliessen; tatsächlich ist dies eine Folge des Durchbruchs der Basis-Emitter-Diode,
die bei den heute meistens verwendeten Planar-Transistoren eine Durchbruchspannung1 von etwa 6 V aufweist.
Bei einem Verstärker haben wir offenbar eine maximale Ausgangsspannung, die
noch keine Verzerrungen aufweist (der Transistor also weder gesperrt noch gesättigt
ist). Es gibt auch eine minimale Ausgangsspannung, die durch das unvermeidliche
Rauschen der Verstärkerstufe festgelegt ist. Rauschsignale sind nicht vorhersagbare, zufällige Signale, die nur mit statistischen Methoden beschrieben werden können. Für das Rauschen gibt es verschiedene Ursachen; dazu gehören das thermische
Rauschen der Widerstände (Brown’sche Bewegung der Leiter-Elektronen), das
Stromrauschen und weitere Rauschursachen in Halbleitern. Sobald das Signal einen
Wert erreicht hat, der in der Grössenordnung des Rauschens liegt, kann das Signal
nicht mehr vom Rauschen unterschieden werden und eine Verstärkung wird sinnlos.
Das Verhältnis von grösstmöglicher zu kleinstmöglicher Signalspannung wird als
Dynamik des Verstärkers bezeichnet. Man ist an einer möglichst grossen Dynamik
interessiert (Beispiel HiFi-Anlagen); da das Rauschen sich unserem Einfluss weitgehend entzieht, kann die Dynamik nur vergrössert werden, wenn die maximal
mögliche Ausgangsspannung so gross wie technisch möglich gewählt wird. Dabei
stellt sich nun die Frage, wie der Arbeitspunkt einer Verstärkerschaltung gewählt
werden muss, damit die unverzerrte Ausgangsspannung so gross wie möglich wird.
Es leuchtet ein, dass das dann der Fall ist, wenn beim gleichen Wert der Eingangsamplitude der Transistor sperrt und sättigt. Für eine quantitative Analyse kann man
die Potentialverläufe für diesen Idealfall einmal skizzieren und dann die
Schlussfolgerungen ziehen (Abbildung 6.15).
1. Dieser Durchbruch kann in Ausnahmefällen auch ausgenutzt werden, sofern sichergstellt
ist, dass der Strom begrenzt bleibt. Man kann einen Transistor mit miteinander verbundenen
Kollektor- und Basis-Anschlüssen auch als Z-Diode für etwa 6 V einsetzen (natürlich nur
als Notmassnahme).
16
Der Transistor als Verstärker
UC
UE
UCC
û2
UCA
UCEA
UEA
û1
GND
t
Abb. 6.15: Optimaler Arbeitspunkt
Die in dieser Abbildung verwendeten Schreibweisen für Spannungen sollen ab jetzt
konsequent verwendet werden. Für die Bedeutung der Schreibweisen gilt, erläutert
am Beispiel der Kollektorspannung:
UC
Momentanwert der Kollektor-Spannung
UCA
Kollektor-Ruhespannung (Arbeitspunkt-Grösse)
uC
Kollektor-Signalspannung (nur Wechselanteil)
Es gilt also auch die Beziehung: UC = UCA + uC
In Abbildung 6.15 erkennt man, dass wegen der Gleichheit von Eingangsspannung
und Emitter-Signalspannung gelten muss: û2 = |vu| û1. Dabei wird mit vu die Spannungsverstärkung bezeichnet. Man kann nun leicht ablesen, dass die KollektorEmitter-Ruhespannung UCEA gleich der halben Betriebsspannung sein muss und
dass das Emitter-Ruhepotential gleich der maximalen Amplitude des Eingangssignals sein muss. Unter Benutzung der eben hergeleiteten Beziehungen erhalten wir
die folgende Gleichung, die erfüllt sein muss, wenn die Schaltung für eine optimale
Aussteuerbarkeit ausgelegt sein soll.
6.2 Einfache Verstärkerschaltung
17
U CC
U EA = -----------------------------2 ⋅ ( 1 + vu )
Diese Beziehung gilt nicht allgemein, sondern nur für die eben untersuchte
Schaltung. Für andere Schaltungen müssen analoge Überlegungen angestellt
werden.
Experiment
Entwurf und Aufbau eines Verstärkers mit aussteuerungsoptimaler Dimensionierung und folgenden Daten: UCC = 12 V, IC . 2 mA, |v| = 10, $min = 100. Gesucht
ist der genaue Messwert für die Spannungsverstärkung v.
+12V
u1
56kΩ
2.7kΩ
1µF
2N2219A
5.6kΩ
270Ω
u2
Abb. 6.16: Verstärker mit v = -10
Die Schaltung von Abbildung 6.16 erfüllt die gestellten Anforderungen hinreichend
gut. Die Messung der Verstärkung an mehreren gleichen Schaltungen ergibt Werte,
die in einem Bereich von 9.3 und etwa 9.7 schwanken, also alle signifikant unter
dem theoretischen Wert von 10 liegen. Die Gründe für diese Abweichung können
nicht in den Widerstandstoleranzen liegen, sonst müssten sicher einzelne Schaltungen auch eine Verstärkung ausweisen, die höher als 10 liegt. Als einzige Erklärung
für diese Abweichung der Messung vom theoretischen Wert bleibt die Vermutung,
dass das bisher verwendete Transistormodell1 das Verhalten des Transistors in
1. Bisher verwendetes Transistor-Modell:
1
Die Spannung UBE zwischen Basis und Emitter ist konstant und beträgt etwa 0.6 bis
0.7 V.
2 Der Kollektorstrom ist proportional zum Basisstrom. Der Proportionalitätsfaktor heisst
Stromverstärkung $ und liegt typisch in der Grössenordnung von 100.
3 Der Emitterstrom IE ist etwa gleich dem Kollektorstrom IC.
4 Der Kollektorstrom ist praktisch unabhängig von der Kollektor-Emitter-Spannung UCE
18
Der Transistor als Verstärker
dieser Anwendung nicht genügend gut beschreibt. Daraus folgt die Notwendigkeit,
ein besseres Modell für den Transistor auszuarbeiten. Man kann dabei vom
bisherigen Modell ausgehen und überprüfen, welche Teile des Modells verfeinert
werden müssen.
Der Punkt (2) dürfte nach wie vor seine Gültigkeit behalten, also auch Bestandteil
des neuen Modells bilden. Was den Punk (3) betrifft, so hat der dadurch gemachte
Fehler (die Vernachlässigung des Basisstromes) die Grösse 1/$, liegt also in der
Grössenordnung von 1%. Da die Messfehler meistens grösser sind, kann auch
dieser Punkt praktisch beibehalten werden. Die Punkte (1) und (4) müssen hingegen
genauer analysiert werden.
6.3
Die Kleinsignal-Ersatzschaltung (KSE)
6.3.1
Der differentielle Basis-Emitter-Widerstand rBE
Die Basis-Emitter-Spannung UBE ist genau genommen nicht konstant, sondern
folgt gemäss der Diodengleichung einer Logarithmus-Funktion (Abbildung 6.17):
UBE
uBE
Näherung (Tangente)
UBEA
Arbeitspunkt
iB
IBA
IB
Abb. 6.17: zur Herleitung von rBE
Der Zusammenhang zwischen IB und UBE ist also nichtlinear. Um die Rechnung zu
vereinfachen, kann man davon ausgehen, dass gemäss den Definitionen aus Kapitel
4 die Signalgrössen als Änderungen um den Arbeitspunkt herum aufgefasst werden
können. Falls nun die Signalamplituden klein sind verglichen zu den Arbeitspunktgrössen, kann die nichtlineare Kennlinie durch ihre Tangente im Arbeitspunkt
approximiert werden. Gleichzeitig kann ein neues Koordinatensystem mit dem
6.3 Die Kleinsignal-Ersatzschaltung (KSE)
19
Ursprung im Arbeitspunkt definiert werden, das als Bezugssystem für die Signalgrössen dient. Auf diese Weise können wir den Zusammenhang zwischen den
Signalgrössen iB und uBE linearisieren und erhalten die folgende Beziehung:
u BE = i B ⋅ rBE
Der Proportionalitätsfaktor rBE heisst differentieller oder dynamischer Basis-Emitter-Widerstand. Seine Grösse kann aus der Diodengleichung bestimmt werden:
u BE
∆U BE
dU BE
rBE = --------- = -------------- = -------------iB
∆I B
dI B
Für die Ableitung der Diodengleichung im Arbeitspunkt erhält man:
⎛ IB⎞
U BE ≈ U T ⋅ ln ⎜ -----⎟
⎝ I S⎠
→
dU BE
------------dIB
IB = I BA
IS 1 UT β ⋅ UT
≈ U T ⋅ -------- ⋅ ---- ≈ -------- ≈ --------------ICA
I BA IS IBA
Bei grösseren Strömen weicht die Diodenkennlinie als Folge von ohmschen Widerständen etwas von der idealen logarithmischen Kennlinie ab; das kann durch folgende Beziehung erfasst werden:
β ⋅ UT
r BE = --------------- + r BB′
I CA
Der Widerstand rBB’ wird innerer Basis-Zuleitungswiderstand genannt und liegt in
der Grössenordnung von 10 ... 100 S. Für kleine Werte von ICA kann also rBB’ ohne
weiteres vernachlässigt werden und man kann mit den folgenden Beziehungen
arbeiten:
u BE = i B ⋅ r BE
β ⋅ UT
r BE ≈ --------------I CA
k⋅T
U T = ---------e
20
Der Transistor als Verstärker
6.3.2
Der differentielle Widerstand rCE
Man kann sich zur Beziehung zwischen Kollektorstrom und Kollektor-EmitterSpannung analoge Überlegungen machen, was dann auf die in Abbildung 6.18
dargestellten Zusammenhänge führt:
IC
iC
ICA
Arbeitspunkt
uCE
UCE
UCEA
Abb. 6.18: zur Definition von rCE
Man erkennt, dass zwischen der Änderung des Kollektorstromes und derjenigen der
Kollektor-Emitterspannung in guter Näherung ein linearer Zusammenhang besteht:
u CE ≈ i C ⋅ r CE
Zur Bestimmung der Grösse des differentiellen Kollektor-Emitter-Widerstandes
rCE kann man das Ausgangskennlinienfeld des Transistors etwas genauer betrachten (Abbildung 6.19). Werden die Ausgangskennlinien nach links verlängert, so
schneiden sich die Verlängerungen näherungsweise in einem Punkt. Da der Anstieg
der Ausgangskennlinien durch den in Kapitel 3 besprochenen Early-Effekt bewirkt
wird, nennt man die Spannung des Schnittpunktes auch Early-Spannung UK. Diese
Spannung hat einen vom Transistortyp abhängigen Wert, der zwischen 50 V und
200 V liegt. Damit kann der Widerstand rCE durch die folgende Beziehung
beschrieben werden:
dU CE
r CE ≈ -------------dIC
IB = I BA
U CE + U K
≈ ------------------------I CA
6.3 Die Kleinsignal-Ersatzschaltung (KSE)
21
IC
ICA
Arbeitspunkt
UCEA
UK (Early-Spannung)
UCE
Abb. 6.19: Bestimmung der Grösse von rCE
Üblicherweise beträgt die Kollektor-Emitter-Ruhespannung UCEA nur wenige Volt,
so dass gilt: UK >> UCEA. Unter Verwendung dieser Beziehung folgt:
UK
r CE ≈ --------I CA
u CE ≈ i C ⋅ r CE
50V ≤ U K ≤ 200V
Der Kollektorstrom IC ist eine Funktion von zwei Variablen: IB und UCE. Damit
erhält man die gesamte Änderung mathematisch durch das vollständige Differential:
i C = f ( I B, U CE )
⇒
∂I C
∂I C
dI C = -------- ⋅ dI B + -------------- ⋅ dU CE
∂I B
∂U CE
Die hier auftretenden partiellen Ableitungen sind nichts anderes als die Stromverstärkung $ bzw. der Kehrwert des differentiellen Kollektor-Emitter-Widerstandes
rCE. Da Änderungen durch Kleinbuchstaben bezeichnet werden, erhält man für
denselben Zusammenhang in der für die Elektronik üblichen Schreibweise:
u CE
i C = β ⋅ i B + ---------r CE
22
Der Transistor als Verstärker
6.3.3
Die Kleinsignal-Ersatzschaltung
Eine Zusammenstellung der bisher gefundenen Beziehungen führt auf das folgende
Gleichungssystem, das das Kleinsignalverhalten des Transistors beschreibt:
u BE = r BE ⋅ i B
u CE
i C = β ⋅ i B + ---------r CE
Die Umsetzung dieses Gleichungssystems in eine elektrische Schaltung ergibt die
folgende Kleinsignal-Ersatzschaltung für den Transistor:
B
iB
Kleinsignal-Ersatzschaltung
iB
uBE
iC
C
β•iB
rBE
rCE
uCE
E
Abb. 6.20: Kleinsignal-Ersatzschaltung (KSE) des Transistors
Auf die folgenden Punkte muss bei jeder Anwendung der KSE geachtet werden, um
grobe Fehler zu vermeiden:
!
Die Kleinsignal-Ersatzschaltung beschreibt nur die Zusammenhänge
zwischen den Änderungen, also den Signalgrössen; sie ist nicht brauchbar für die Berechnung von Arbeitspunktgrössen.
!
Die Bezugsrichtungen für iB und $ iB sind integrierende Bestandteile der
KSE und dürfen keinesfalls weggelassen werden. Sie bestimmen die
gegenseitige Phasenlage von iB und iC.
!
Die Stromquelle ist eine stromgesteuerte Stromquelle (CCCS = Current
Controlled Current Source). Bei Anwendung des Überlagerungssatzes ist
daher äusserste Vorsicht geboten.
!
Die KSE ist nur gültig, wenn die Kleinsignal-Bedingung eingehalten
wird, wenn also die Amplituden der Signale relativ klein sind verglichen
mit den Arbeitspunkt-Grössen. Wenn diese Bedingungen nicht eingehalten werden, resultieren daraus entsprechende Fehler.
6.3 Die Kleinsignal-Ersatzschaltung (KSE)
!
23
Die Kleinsignal-Ersatzschaltungen von npn- und pnp-Transistoren unterscheiden sich nicht; die Unterschiede betreffen nur die Vorzeichen der
Arbeitspunkt-Grössen.
Die eben hergeleiteten Parameter der KSE werden in der Elektronik-Literatur auch
etwa mit anderen Bezeichnungen versehen (häufig werden die sogenannten Hybridoder h-Parameter aus der allgemeinen Vierpol-Theorie verwendet). Die folgende
Tabelle vermittelt einen Überblick über die entsprechenden Bezeichnungen:
Äquivalente Bezeichnungen für die Transistor-Parameter:
Basis-Emitter-Widerstand
Stromverstärkung
Kollektor-Emitter-Widerstand
rBE
h11
hie
$
h21
hfe
rCE
1/h22
1/hoe
Bemerkenswert ist noch die Tatsache, dass sich die Parameter der KleinsignalErsatzschaltung aus den Arbeitspunkt-Grössen, aus der Stromverstärkung $ sowie
aus den “Naturkonstanten” UT und UK berechnen lassen. Aus diesem Grund findet
man häufig in Datenblättern auch keine diesbezüglichen Angaben.
Mit Hilfe der Transistor-Ersatzschaltung lassen sich nun auch für ganze Verstärkerstufen Kleinsignal-Ersatzschaltungen zeichnen und damit auch die resultierenden
Parameter eines Verstärkers einfacher und genauer bestimmen. Die genaue Vorgehensweise soll anhand einiger Beispiele gezeigt und geübt werden.
24
Der Transistor als Verstärker
6.4
Die Emitterschaltung
6.4.1
Emitterschaltung ohne AC-Gegenkopplung
Zur Erzielung einer möglichst grossen Spannungsverstärkung müsste in der bisher
betrachteten Schaltung das Verhältnis RC/RE möglichst gross werden. Veränderungen der Widerstände führen aber zu nicht akzeptablen Änderungen der Arbeitspunkt-Grössen. Um die Verstärkung zu vergrössern, würde es genügen, wenn der
Widerstand RE nur für Wechselsignale klein wird, für Gleichstrom (Arbeitspunkt)
seinen Wert aber beibehält, damit ein in jeder Hinsicht stabiler Arbeitspunkt eingestellt werden kann. Man kann das erreichen, indem parallel zu RE ein Kondensator
CE geschaltet wird; die Impedanz dieser Parallelschaltung ist dann für hinreichend
hohe Frequenzen praktisch vernachlässigbar. Die folgende Schaltung (Abbildung
6.21) ist gemäss dieser Idee konzipiert; als Neuerung wurde hier einmal die
Betriebsspannungsquelle mit eingezeichnet.
R1
RC
URCA
UCC
C1
u1
R2
RE
u2
CE
Abb. 6.21: Emitterschaltung ohne AC-Gegenkopplung
Zum Zeichnen der Ersatzschaltung für die ganze Verstärkerstufe geht man zweckmässigerweise wie folgt vor:
1.
Die Spannungsquelle UCC ist für Signale ein Kurzschluss. Alle mit UCC
verbundenen Punkte der Schaltung liegen also signalmässig an Masse.
2.
Kondensatoren werden in erster Näherung als Kurzschlüsse für Signale
betrachtet.
3.
Das Transistor-Symbol wird durch die Kleinsignal-Ersatzschaltung ersetzt.
4.
Umzeichnen der Schaltung unter Erhaltung der topologischen
Zusammenhänge.
6.4 Die Emitterschaltung
25
Unter Beachtung der obigen Regeln erhält man die folgende Ersatzschaltung für die
Verstärkerstufe:
β iB
iB
u1
R1
R2
rBE
RC
rCE
u2
Abb. 6.22: KSE der Verstärkerstufe
Durch Zusammenfassen von Widerständen (R1 || R2 = Rp, RC || rCE = R’C) lässt sich
diese Ersatzschaltung noch weiter vereinfachen:
β iB
iB
u1
Rp
rBE
R’C
u2
Abb. 6.23: Vereinfachte KSE
Ausgehend von dieser Ersatzschaltung kann nun die Spannungsverstärkung leicht
berechnet werden. Ein- und Ausgangsspannung lassen sich durch iB ausdrücken:
u 1 = i B ⋅ r BE
u 2 = – β ⋅ i B ⋅ R' C
Damit erhält man für die Spannungsverstärkung vu:
β ⋅ R' C
u2
v u = ----- = – ---------------r BE
u1
Bei einer oberflächlichen Betrachtung dieser Beziehung könnte man denken, dass
die Spannungsverstärkung der Stufe proportional zur Stromverstärkung des Transistors ist, was eigentlich auch einleuchtend erscheint. Die erhaltenen Ausdrücke
müssen solange umgeformt werden, bis keine berechenbaren Grössen wie rBE oder
rCE mehr auftreten, da diese Grössen arbeitspunktabhängig sind. Es sollten nur
noch Konstanten wie $ oder UK sowie Arbeitspunktgrössen auftreten.
26
Der Transistor als Verstärker
Durch Einsetzen der entsprechenden Beziehungen erhält man neu:
β ⋅ R' C
β ⋅ R'C
ICA ⋅ R' C
v u = – ---------------- = – ---------------- = – ---------------------r BE
β⋅U
UT
--------------TICA
Durch Einsetzen für R’C und unter Ausnutzung der Beziehung rCE = UK/ICA erhält
man schliesslich:
I CA ⋅ R' C
I CA ⋅ R C ⋅ r CE
UK
U RCA
v u = – ---------------------- = – --------------------------------------- = – -------------- ⋅ ----------------------------UT
U T ⋅ ( R C + r CE )
U T U K + U RCA
Als endgültigen Ausdruck für die Spannungsverstärkung der betrachteten Emitterschaltung erhält man also:
u2
U RCA
UK
v u = ----- = – -------------- ⋅ ----------------------------u1
U T U K + U RCA
Die Spannungsverstärkung ist im wesentlichen proportional zur Ruhespannung
über dem Kollektorwiderstand (URCA = ICA · RC) und umgekehrt proportional zur
Temperaturspannung UT. Der zweite Term im obigen Ausdruck beschreibt den Einfluss von rCE; unter Berücksichtigung der Grössenverhältnisse (UK = 50 ... 200 V,
URCA = wenige V) ist dieser Korrekturfaktor ziemlich nahe bei 1. Der Einfluss von
rCE ist also in vielen Fällen vernachlässigbar klein. Überraschenderweise ist aber
die Spannungsverstärkung überhaupt nicht von der Stromverstärkung $ des Transistors abhängig.
Zwecks Überprüfung dieses Resultates wurde die Schaltung von Abbildung 159 mit
folgenden Elementwerten aufgebaut: R1 = 120 kS, R2 = 22 kS, RC = 5.6 kS,
RE = 1.8 kS, UCC = 15 V, C1 = 1 µF, CE = 100 µF.
Die Messung der Ruhespannung URCA ergab einen Wert von 5.1 V. Mit
UT = 26 mV und einem geschätzten Wert von UK = 100 V ergibt sich für den
erwarteten Wert der Spannungsverstärkung etwa -185. Die gemessenen Kurvenformen von u1(t) und u2(t) sind in Abbildung 6.24 dargestellt; als Eingangsspannung
wurde wieder eine Dreieck-Spannung verwendet.
6.4 Die Emitterschaltung
u1(t)
27
u2(t)
30mV
10V
20mV
8V
10mV
6V
0V
4V
-10mV
2V
-20mV
0V
-30mV
-2V
-40mV
-4V
-6V
-50mV
10µs/DIV
Abb. 6.24: Spannungsverläufe bei der Emitterschaltung
Die Messung der Spannungsverstärkung aus den Kurvenformen ergibt einen Wert
von -182; die Messung zeigt also eine sehr gute Übereinstimmung mit der Theorie.
Auffallend ist, dass die Ausgangsspannung ziemlich verzerrt scheint; anstelle der
erwarteten Dreieck-Spannung erscheinen Kurvenformen, die an gotische Kirchenfenster erinnern. Diese nichtlinearen Verzerrungen sollen jetzt etwas näher untersucht werden. Als Mass für die nichtlinearen Verzerrungen hat sich der Klirrfaktor
eingebürgert.
Klirrfaktor
Zur Definition des Klirrfaktors d (distortion factor, auch Total Harmonic Distortion THD genannt) geht man von der Tatsache aus, dass jede periodische Funktion
durch eine Summe von harmonischen Schwingungen mit ganzzahligen Vielfachen
der Grundfrequenz dargestellt werden kann (Fourier-Reihe). Es gilt also für eine
periodische Funktion x(t):
∞
x ( t ) = a0 +
∑ an ⋅ cos ( n ⋅ ωt + ϕn )
n=1
28
Der Transistor als Verstärker
Die Koeffizienten an sind also die Amplituden der einzelnen harmonischen Schwingungen; die Schwingung mit der Frequenz T wird Grundwelle genannt, die
Schwingungen mit den Frequenzen n@T mit n > 1 werden als Oberwellen bezeichnet. Der Klirrfaktor ist ein Mass für die Abweichung eines Signals von der reinen
Sinus-Form und ist wie folgt definiert:
2
2
2
2
a 2 + a 3 + ...
a 2 + a 3 + ...
d = -------------------------------------- ≈ -----------------------------------------------2
2
2
a1
a 1 + a 2 + a 3 + ...
Die beiden Definitionen sind für kleine Werte von d (d < 10%) praktisch gleichwertig. Der Klirrfaktor dient auch als Mass für die von einer Verstärkerstufe
verursachten Verzerrungen. Man geht davon aus, dass das Eingangssignal rein harmonisch sei, bestimmt den Klirrfaktor des Ausgangssignals und bezeichnet diesen
Wert dann auch als Klirrfaktor des Verstärkers.
In der Emitterschaltung ist der Zusammenhang zwischen Kollektorstrom iC und der
Ausgangsspannung u2 mit Sicherheit linear; ebenso kann der Zusammenhang zwischen iB und iC als praktisch linear angenommen werden. Die beobachteten nichtlinearen Verzerrungen müssen also durch die Nichtlinearität der Kennlinie der BasisEmitter-Diode verursacht worden sein. Für diese Kennlinie kann man gemäss der
bekannten Diodengleichung den folgenden Ansatz machen:
⎛ U BE⎞
⎛ U BEA + u BE⎞
I B = IS ⋅ exp ⎜ -----------⎟ = I S ⋅ exp ⎜ ------------------------------⎟
UT
⎝ UT ⎠
⎝
⎠
⎛ U BEA⎞
⎛ u BE⎞
⎛ u BE⎞
IB = I S ⋅ exp ⎜ --------------⎟ ⋅ exp ⎜ ---------⎟ = I BA ⋅ exp ⎜ ---------⎟
⎝ UT ⎠
⎝ UT ⎠
⎝ UT ⎠
Die letzte Exponentialfunktion kann durch eine Potenz-Reihe (Taylor-Reihe) dargestellt werden:
∞
exp ( x ) =
∑
n=0
n
x2 x3 x 4
x
----- = 1 + x + ----- + ----- + ------ + ...
2
6 24
n!
6.4 Die Emitterschaltung
29
Damit erhält man für den resultierenden Basis-Strom IB den folgenden Ausdruck:
⎛ u BE⎞
I B = I BA ⋅ exp ⎜ ---------⎟ = I BA + i B
⎝ UT ⎠
⎛ u BE⎞ 1 ⎛ u BE⎞ 2 1 ⎛ u BE⎞ 3
IB = I BA ⋅ 1 + ⎜ ---------⎟ + --- ⋅ ⎜ ---------⎟ + --- ⋅ ⎜ ---------⎟ + ...
6 ⎝ UT ⎠
⎝ UT ⎠ 2 ⎝ UT ⎠
⎛ u BE⎞ 1 ⎛ u BE⎞ 2 1 ⎛ u BE⎞ 3
I B = IBA + I ⋅ ⎜ ---------⎟ + --- ⋅ ⎜ ---------⎟ + --- ⋅ ⎜ ---------⎟ + ...
BA ⎝ U ⎠ 2 ⎝ U ⎠
6 ⎝ UT ⎠
T
T
Der Wechsel- oder Signalanteil iB ist demnach gegeben durch:
⎛ u BE⎞ 1 ⎛ u BE⎞ 2 1 ⎛ u BE⎞ 3
i B = I BA ⋅ ⎜ ---------⎟ + --- ⋅ ⎜ ---------⎟ + --- ⋅ ⎜ ---------⎟ + ...
6 ⎝ UT ⎠
⎝ UT ⎠ 2 ⎝ UT ⎠
Mit dem Ansatz uBE = ûBE·cos(Tt) erhält man für iB:
2
⎛ û BE⎞
2
1--- ⎛ û BE⎞
i B = I BA ⋅ ⎜ ---------⎟ ⋅ cos ( ωt ) + ⋅ ⎜ ---------⎟ ⋅ ( cos ( ωt ) ) + ...
2 ⎝ UT ⎠
⎝ UT ⎠
Da man bereits jetzt mit Sicherheit sagen kann, dass ûBE << UT ist, kann die Reihe
ohne nennenswerten Fehler nach dem zweiten Glied abgebrochen werden. Unter
Berücksichtigung der trigonometrischen Beziehung
2
1
( cos ( ωt ) ) = --- ( 1 + cos ( 2ωt ) )
2
erhält man für die Reihenentwicklung des Basis-Stromes iB:
2
⎛ û BE⎞ 2
⎛ ⎛ û BE⎞
⎞
1--- ⎛ û BE⎞
1
i B ≈ I BA ⋅ ⎜ ⎜ ---------⎟ ⋅ cos ( ωt ) + ⋅ ⎜ ---------⎟ + --- ⋅ ⎜ ---------⎟ ⋅ cos ( 2ωt )⎟
4 ⎝ UT ⎠
4 ⎝ UT ⎠
⎝⎝ UT ⎠
⎠
30
Der Transistor als Verstärker
Für den Klirrfaktor d der Schaltung folgt daraus durch Vergleich mit der FourierReihe:
a2
û BE
d ≈ ----- = -------------a1
4 ⋅ UT
Daraus folgt, dass die Amplitude der Eingangsspannung maximal ca. 1 mV
betragen darf, wenn der Klirrfaktor des Verstärkers weniger als 1% betragen soll
( ûBE = 4·UT·d = 4·26 mV·0.01 = 1.04 mV). Der Klirrfaktor wächst proportional zur
Amplitude der Eingangsspannung.
Allgemeine Verstärker-Kenngrössen
Bis jetzt wurde ein Verstärker lediglich durch seine Spannungsverstärkung vu
beschrieben. Ein Verstärker hat aber auch einen endlichen Eingangswiderstand rein.
Ausgangsseitig kann er als aktiver Zweipol betrachtet werden mit einer idealen
Spannungsquelle vu·u1 und einem Innenwiderstand raus (Ausgangswiderstand). Ein
rückwirkungsfreier Verstärker kann also durch die folgende Ersatzschaltung
beschrieben werden:
Verstärker
u1
rein
ue
raus
vu ue
u2
Abb. 6.25: Ersatzschaltung eines Verstärkers
Das Kleinsignalverhalten eines Verstärkers wird also durch die drei Parameter
Spannungsverstärkung vu, Eingangswiderstand rein und Ausgangswiderstand raus
beschrieben. Alle drei Parameter sind gleich wichtig; es wäre falsch, die Qualität
eines Verstärkers etwa nur aufgrund seiner Spannungsverstärkung zu beurteilen.
Man kann das leicht erkennen, wenn man verschiedene Fälle untersucht, in denen
auch die Signalquellen einen hohen Innenwiderstand aufweisen (z.B. der KristallTonabnehmer eines Plattenspielers oder ein Piezo-Drucksensor).
6.4 Die Emitterschaltung
31
Aus der Ersatzschaltung der Emitterschaltung (Abbildung 6.23) kann man leicht die
Werte für Ein- und Ausgangswiderstand entnehmen:
r ein = R p || r BE ≈ r BE
r aus = R C || r CE ≈ R C
Messung von Ein- und Ausgangswiderstand
Da es sich bei Ein- und Ausgangswiderstand um differentielle Widerstände handelt,
können sie nicht mit dem Ohm-Meter gemessen werden. Im folgenden sollen zwei
zur Messung des Eingangswiderstandes geeignete Schaltungen vorgestellt werden.
Die erste Schaltung beruht auf einem Vergleich des Eingangswiderstandes mit
einem bekannten Widerstand:
S
R
C
u0
u2 V
Abb. 6.26: Messung des Eingangswiderstandes
Zur Messung wird erst der Schalter S geschlossen und die resultierende Ausgangsspannung u2 = u20 wird abgelesen. Sodann wird S geöffnet und der Widerstand R
solange verändert, bis die Ausgangsspannung u2 = u20/2 beträgt. Das bedeutet, dass
auch die Eingangsspannung des Verstärkers genau die Hälfte des vorherigen Wertes
sein muss, was genau dann der Fall ist, wenn R = rein ist. Der Widerstand R kann
nun mit einem Ohm-Meter gemessen werden. Für die Messung sollte die Ausgangsspannung mit dem Oszilloskop überwacht werden, denn eine Messung liefert
nur dann vernünftige Resultate, wenn der Verstärker nicht übersteuert wird. Der
veränderliche Widerstand R sollte eher durch ein Schichtpotentiometer realisiert
werden als durch ein präzises Zehngang-Potentiometer. Letztere bestehen aus einer
Doppelwendel aus Widerstandsdraht, bilden also eigentliche lange zylindrische
Luftspulen, deren Induktivität bei den hier auftretenden Frequenzen nicht mehr
ohne weiteres vernachlässigt werden darf. Die Impedanz von C bei der Messfrequenz muss viel kleiner sein als der erwartete Wert von rein.
32
Der Transistor als Verstärker
Ein alternatives Messverfahren beruht auf der Idee, den Eingangsklemmen einen
Signalstrom einzuprägen und den dabei entstehenden Spannungsabfall an den Eingangsklemmen zu messen. Das führt auf die folgende Schaltung:
i1
C
RV
u0
u1
Abb. 6.27: Alternatives Messverfahren
Unter der Voraussetzung RV >> rein und damit u0 >> u1 gilt also:
u1 ⋅ Rv
u1
u1
r ein = ----- = ----------------- ≈ R v ⋅ ----u0 – u 1
i1
u0
Die Messung des Ausgangswiderstandes erfolgt analog durch Einspeisen eines
Stromes in den Ausgang (Abbildung 6.28). Die Eingangsklemmen werden dabei
mit einem Widerstand RQ abgeschlossen, der dem Innenwiderstand der normalerweise angeschlossenen Signalquelle entspricht.
i2
C
RQ
RV
u2
u0
Abb. 6.28: Messung des Ausgangswiderstandes
Wenn auch hier die Voraussetzungen RV >> raus und damit u0 >> u2 erfüllt sind, so
gilt für den Ausgangswiderstand raus:
Rv ⋅ u2
u2
u2
r aus = ----- = ----------------- ≈ R v ⋅ ----u0 – u 2
i2
u0
6.4 Die Emitterschaltung
6.4.2
33
Emitterschaltung mit Stromgegenkopplung
Die Methode der Kleinsignal-Ersatzschaltung soll nun auch noch auf die einfache
Verstärkerschaltung von Abschnitt 6.2 angewendet werden. Hier nochmals die
Schaltung:
UCC
R1
RC
URCA
C1
u1
R2
RE
UREA
u2
Abb. 6.29: Emitterschaltung mit Gegenkopplung
Zur Analyse dieser Schaltung wird zunächst gemäss den bekannten Regeln die
Kleinsignal-Ersatzschaltung gezeichnet:
rBE
u1
Rp
iB
βiB
RE
rCE
RC
u2
Abb. 6.30: KSE der Emitterschaltung mit Stromgegenkopplung
Die Berechnung z. B. der Spannungsverstärkung kann nun nicht mehr so einfach
erfolgen, wie im vorhergehenden Beispiel. Man kann aber alle aus der Elektrizitätslehre bekannten Verfahren der Netzwerkanalyse auch auf KleinsignalErsatzschaltungen anwenden. Zur Analyse der vorliegenden Schaltung eignet sich
das Kreisstrom-Verfahren besonders gut. Zur Anwendung des Kreisstrom-Verfahrens muss aber die Ersatzschaltung noch etwas modifiziert werden, da Stromquellen
schlecht zur Methode passen. Durch Umwandlung der gesteuerten realen Stromquelle in eine gesteuerte reale Spannungsquelle erhält man die folgende neue
Ersatzschaltung:
34
Der Transistor als Verstärker
rBE
u1
rCE
iB
Rp
βrCEiB
RE
RC
u2
Abb. 6.31: Modifizierte Ersatzschaltung
Der Widerstand Rp liegt parallel zu einer idealen Spannungsquelle, hat also keinen
Einfluss auf Ströme und Spannungen im übrigen Netzwerk und darf daher weggelassen werden. Nach Einzeichnen des Baumes (fett) und der Kreisströme j1 und j2
resultiert die zur Formulierung der Netzwerk-Gleichungen geeignete Ersatzschaltung:
rBE
u1
j1
βrCEiB
rCE
iB
RE
j2
RC
u2
Abb. 6.32: Ersatzschaltung für die Anwendung der Kreisstrom-Analyse
Aus der Schaltung können die Netzwerkgleichungen formuliert werden (hier sind
es Maschensätze):
j 1 ⋅ ( rBE + R E ) + j 2 ⋅ ( – RE ) = u 1
j 1 ⋅ ( – R E ) + j 2 ⋅ ( r CE + R C + R E ) = – β ⋅ i B ⋅ r CE
Da offensichtlich iB gleich dem Kreisstrom j1 ist, kann das Gleichungssystem noch
entsprechend umgeschrieben werden. Man erhält also das folgende endgültige
lineare Gleichungssystem für die beiden Kreisströme:
j 1 ⋅ ( rBE + R E ) + j 2 ⋅ ( – RE ) = u 1
j 1 ⋅ ( β ⋅ r CE – R E ) + j 2 ⋅ ( r CE + R C + RE ) = 0
6.4 Die Emitterschaltung
35
Zur Berechnung der Ausgangsspannung u2 benötigen wir den Kreisstrom j2, also
lösen wir das Gleichungssystem mit Hilfe der Regel von Cramer nach j2 auf:
( r BE + R E )
u1
( β ⋅ r CE – RE ) 0
– u1 ⋅ ( βr CE – RE )
- = -----------------------------------------------------------------------------------------------------------j 2 = ------------------------------------------------------------------------( r BE + R E )
( – RE )
( r BE + RE ) ( r CE + RC + R E ) + R E ( βr CE – R E )
( βr CE – RE ) ( r CE + R C + R E )
Mit u2 = j2·RC erhält man schliesslich für die Spannungsverstärkung vu:
u2
– R C ( βr CE – R E )
v u = ----- = -----------------------------------------------------------------------------------------------------------------u1
( r BE + R E ) ( r CE + R C + R E ) + R E ( βr CE – R E )
Der Ausdruck ($rCE - RE) soll noch näher untersucht werden. Unter Verwendung
bekannter Beziehungen findet man:
βU K U REA βU K
βr CE – R E = ----------- – -------------- ≈ ----------- = βr CE
I CA
I CA
I CA
Unter Verwendung dieser Vereinfachung erhält man für die Verstärkung:
u2
– βr CE R C
v u = ----- = -----------------------------------------------------------------------------------------------u1
( r BE + R E ) ( r CE + R C + R E ) + βr CE R E
Dieses Resultat ist nun nicht einfach interpretierbar. Aus der allerersten Analyse der
Schaltung unter Annahme eines idealen Transistors (Abschnitt 6.2) kennt man die
ideale Spannungsverstärkung vu = - RC / RE. Die Spannungsverstärkung kann nun
als Produkt dieser idealen Verstärkung mit einem Korrekturfaktor aufgefasst werden; durch Ausklammern von videal = - RC / RE erhält man:
u2
RC
1
v u = ----- = – ------- ⋅ -----------------------------------------------------------------------------------u1
RE
⎛ ( r BE + R E ) ( r CE + R C + RE )⎞
1 + ⎜ ---------------------------------------------------------------------⎟
βr CE R C
⎝
⎠
36
Der Transistor als Verstärker
Der Klammerausdruck im Nenner des Korrekturfaktors kann nun etwas genauer
untersucht werden:
r BE + R E r CE + R C + RE
( r BE + R E ) ( r CE + RC + R E )
--------------------------------------------------------------------- = --------------------- ⋅ -----------------------------------βrCE R E
βR E
r CE
U REA + U RCA⎞
⎛ βU T + U REA⎞ ⎛
= ⎜ --------------------------------⎟ ⋅ ⎜ 1 + -----------------------------------⎟
UK
⎝ βU REA ⎠ ⎝
⎠
U REA + U RCA⎞
⎛ UT
1⎞ ⎛
= ⎜ -------------- + ---⎟ ⋅ ⎜ 1 + -----------------------------------⎟
UK
⎠
⎝ U REA β⎠ ⎝
Dieser Ausdruck ist offensichtlich viel kleiner als 1, damit kann man auch den
ursprünglichen Ausdruck für die Spannungsverstärkung durch Verwendung einer
Näherung noch einfacher schreiben:
U REA + U RCA⎞
RC
⎛ UT
1-⎞ ⎛
------------------vu = –
⋅ 1–⎜
+ ⎟ ⋅ ⎜ 1 + -----------------------------------⎟
UK
RE
U
⎝ REA β⎠ ⎝
⎠
Die Abweichung der Verstärkung vom idealen Wert wird massgeblich durch die
Ruhespannung über dem Emitterwiderstand bestimmt. Der Verstärkungsfehler wird
umso kleiner, je grösser diese Ruhespannung ist. Die Stromverstärkung $ des Transistors hat einen relativ kleinen Einfluss. Einen fast völlig vernachlässigbaren Einfluss auf die Spannungsverstärkung hat rCE, der entsprechende Term im obigen
Ausdruck stellt eigentlich nur den Fehler des Fehlers dar. Zur Kontrolle kann man
die Werte der Schaltung von Abbildung 6.16 verwenden: UREA = 0.5 V, URCA = 5
V, $ > 100, UK = 100 V, RC / RE = 10. Man erhält für die erwartete Spannungsverstärkung einen Wert von -9.35, was recht gut den seinerzeit gemessenen Werten
entspricht.
Zur Berechnung des Eingangswiderstandes rein der Schaltung kann man nochmals
die Kleinsignalersatzschaltung von Abbildung 6.31 betrachten. Man erkennt leicht,
dass der Eingangswiderstand gleich der Parallelschaltung von Rp mit dem
“inneren” Eingangswiderstand r’ein=u1/iB ist. Der Strom iB ist gleich dem Kreisstrom j1, so dass man das Gleichungssystem wieder nach der Regel von Cramer
nach j1 auflösen kann:
6.4 Die Emitterschaltung
u1
37
–RE
u 1 ⋅ ( r CE + R C + RE )
0 ( r CE + RC + RE )
j 1 = -------------------------------------------------------------------------- = ------------------------------------------------------------------------------------------------------------( r BE + R E )
( – RE )
( r BE + RE ) ( r CE + RC + R E ) + R E ( βr CE – R E )
( βr CE – RE ) ( r CE + R C + R E )
Damit erhält man für r’ein:
u1
( r BE + R E ) ( r CE + R C + R E ) + R E ( βr CE – R E )
r'ein = ----- = -----------------------------------------------------------------------------------------------------------------j1
( r CE + R C + R E )
βr CE R E
= r BE + R E + -----------------------------------R +R +r
E
C
CE
r CE
⎛
⎞
= r BE + R E + βR E ⋅ ⎜ ------------------------------------⎟
⎝ RE + R C + r CE⎠
UK
⎛
⎞
-------------------------------------------------⎟
= r BE + R E + βR E ⋅ ⎜
⎝ U REA + U RCA + U K⎠
Unter Beachtung der Grössenverhältnisse (UK >> UREA , URCA) erhält man als gute
Näherung:
r' ein ≈ r BE + β ⋅ R E ≈ β ⋅ R E
Daraus lässt sich nun der resultierende Eingangswiderstand der Emitterschaltung
mit Stromgegenkopplung berechnen:
r ein ≈ R p || β ⋅ R E
In vielen praktischen Fällen ist Rp << $ RE; der Eingangswiderstand wird dann
praktisch nur noch durch den resultierenden Widerstand des Basisspannungsteilers
Rp bestimmt.
38
Der Transistor als Verstärker
Der Ausgangswiderstand raus ist ziemlich aufwendig zu berechnen, die Berechnung
soll deshalb hier übergangen werden. Als Resultat erhält man die folgende
Näherung:
r aus ≈ RC
6.4.3
Einfluss der Kondensatoren
Die in den Schaltungen enthaltenen Kondensatoren beeinflussen den Frequenzgang
der Verstärkerstufen. Damit die Kondensatoren dimensioniert werden können, muss
man zuerst den Frequenzgang berechnen. Als Beispiel diene hier wieder die Emitterschaltung ohne AC-Gegenkopplung (Abschnitt 6.4.1):
UCC
R1
RC
URCA
C1
u1
u2
R2
u3
UREA
RE
CE
Abb. 6.33: Schema für den Frequenzgang
Zur Berechnung des Frequenzganges kann man so vorgehen, dass man den Einfluss
der einzelnen Kondensatoren getrennt untersucht. Man kann einmal annehmen,
dass der Kondensator CE für Wechselsignale einen Kurzschluss bildet. Unter dieser
Voraussetzung beträgt die Verstärkung u3/u2 gemäss früherer Rechnungen:
U RCA
u3
----- ≈ – -------------u2
UT
6.4 Die Emitterschaltung
39
Für die uns interessierende Spannungsverstärkung u3/u1 kann man schreiben:
u3
u u
----- = -----2 ⋅ -----3
u1
u1 u 2
Einfluss von C1
Der erste Faktor u2/u1 erfasst den Einfluss des Koppelkondensators C1, und zwar
bildet C1 mit dem Eingangswiderstand der Verstärkerstufe einen Spannungsteiler,
wie er in Abbildung 6.34 dargestellt ist.
C1
U1
rein
U2
Abb. 6.34: RC-Hochpass
Zur Berechnung der Frequenzgänge muss die komplexe Wechselstromrechnung
angewendet werden, man arbeitet deshalb mit Zeigern (Zeiger U stellen ja definitionsgemäss harmonische Wechselgrössen dar, sind also etwa gleichwertig zu den
bisher verwendeten Kleinsignalgrössen u). Mit Hilfe der komplexen Rechnung
erhält man für den Frequenzgang des RC-Hochpasses:
ω
j --------U2
r ein
jωr ein C 1
ω c1
------- = ---------------------------- = ------------------------------- = -------------------ω
U1
1
1
+
jωr
C
ein 1
1 + j --------r ein + ------------ω c1
jωC 1
1
ω c1 = ---------------r ein C 1
Der Amplitudengang dieser Funktion hat den in Abbildung 6.35 gezeigten Verlauf.
Bevor dieses Resultat noch interpretiert wird, soll der Einfluss des Emitterkondensators CE untersucht werden.
40
Der Transistor als Verstärker
1
U2/U1
0.1
0.01
0.01
0.1
1
10
100
ω/ωc1
Abb. 6.35: Amplitudengang des RC-Hochpasses
Einfluss von CE
Bevor man mit der eigentlichen Rechnung beginnt, sollte aufgrund von physikalischen Überlegungen die “Form” des Amplitudenganges ermittelt werden. Für sehr
tiefe Frequenzen kann der Kondensator CE als sehr große Impedanz betrachtet werden; in diesem Fall erhält man für den Betrag der Verstärkung etwa den Wert von
RC/RE (Emitterschaltung mit Gegenkopplung), also einen relativ kleinen Wert. Für
sehr hohe Frequenzen hingegen bildet CE einen Kurzschluss und die Verstärkung
beträgt URCA/UT, also viel mehr als bei tiefen Frequenzen. Zwischen diesen beiden
asymptotischen Werten muss der Amplitudengang mit 20 dB/Dekade steigen; man
erhält daraus die in Abbildung 6.36 dargestellte Skizze des Amplitudenganges.
U3/U2
B
A
ωc3
0dB
ω
ωc2
C
Abb. 6.36: Skizze des Amplitudenganges
6.4 Die Emitterschaltung
41
Wie in der Skizze angedeutet, kann der Frequenzgang in ein Produkt elementarer
Frequenzgänge zerlegt werden. Für die entsprechenden Frequenzgänge GA(T),
GB(T) und GC(T) kann man ansetzen:
GA ( ω ) = k
ω
G B ( ω ) = 1 + j --------ω c2
1
G C ( ω ) = ------------------------ω
1 + j ⋅ --------ω c3
Der resultierende Frequenzgang ist gleich dem Produkt der elementaren Frequenzgänge, hat also die folgende mathematische Struktur:
ω
1 + j ⋅ --------U3
ω c2
------- = -----------------------U2
ω
1 + j ⋅ --------ω c3
Nun kann der genaue Frequenzgang mit Hilfe der Kleinsignalersatzschaltung
(Abbildung 6.37) berechnet werden. Um die Rechnung zu vereinfachen, wurde der
dynamische Kollektor-Emitter-Widerstand rCE in der KSE weggelassen, da sein
Einfluss gemäss unseren bisherigen Erfahrungen vernachlässigbar klein ist. Die
Parallelschaltung RE||CE wurde durch die Impedanz ZE berücksichtigt.
rBE
U2
IB
Rp
βIB
ZE
RC
U3
Abb. 6.37: KSE für Frequenzgangberechnung
Aus dieser Ersatzschaltung können direkt die folgenden Beziehungen für die Einund die Ausgangsspannung entnommen werden:
U 2 = I ⋅ ( r BE + ( 1 + β ) ⋅ Z E )
B
Daraus folgt für die Spannungsverstärkung der Stufe:
U3
–β ⋅ RC
------- ≈ ----------------------------U 2 r BE + β ⋅ Z E
U3 = – I ⋅ β ⋅ RC
B
42
Der Transistor als Verstärker
Durch Einsetzen für die Emitterimpedanz ZE folgt weiter:
U3
–RC
– R C ⋅ ( 1 + jωR E C E )
------- = --------------------------------------------- = --------------------------------------------------------U2
RE
r BE
r BE
------------------------------ + --------R E + --------- ( 1 + jωR E C E )
1 + jωR E C E
β
β
Durch Ausklammern im Nenner kann der Ausdruck in die gewünschte Form
gebracht werden:
ω
1 + j ⋅ --------U3
ω c2
–RC
1 + jωR E C E
------- = ---------------------⋅ ------------------------------------------------------- = – k ⋅ ------------------------ω
U2
r BE
⎛ R E ⋅ r BE ⎞
1 + j ⋅ --------R E + --------- 1 + jωC ⎜ ------------------------ω c3
E βR + r ⎟
β
⎝ E
BE⎠
Das Minuszeichen beim Ausdruck für die Verstärkung stört hier nicht, es bedeutet
ja nur eine Phasenverschiebung um B; für den Amplitudengang sind nur die
Beträge massgebend.
Durch Koeffizientenvergleich findet man für die Konstante k und die erste Eckfrequenz Tc2:
RC
RC
--------------------------k =
≈ r BE R E
R E + --------β
1
ω c2 = -------------RE CE
Die zweite Eckfrequenz Tc3 muss etwas genauer betrachtet werden; man erhält
dafür unter Berücksichtigung der Grössenverhältnisse:
I CA ⎞
ICA
1 β
1
1 ⎛ I CA 1 ⎞
1 ⎛ I CA
ω c3 = ------- ⎛ --------- + -------⎞ = ------- ⎜ --------- + -------⎟ = ------- ⎜ --------- + --------------⎟ ≈ ------------------C E ⎝ r BE R E⎠
C E ⎝ U T R E⎠
C E ⎝ U T U REA⎠ U T ⋅ C E
Der Kondensator CE führt also ebenfalls zu einem hochpassartigen Verhalten der
Verstärkerstufe.
6.4 Die Emitterschaltung
43
Resultierender Amplitudengang
Den resultierenden Amplitudengang der gesamten Verstärkerstufe erhält man durch
grafische Addition der beiden Teil-Amplitudengänge. Der Verstärker soll natürlich
in dem Frequenzbereich betrieben werden, bei dem die Verstärkung einen konstanten hohen Wert hat. Die untere Grenzfrequenz eines Verstärkers ist definiert als
die Frequenz, bei der die Ausgangsleistung noch die Hälfte der Ausgangsleistung
im Betriebsfrequenzbereich beträgt. Bei der Grenzfrequenz Tgu = 2Bfgu tritt also
eine Dämpfung von 3 dB gegenüber dem Durchlassbereich auf. Die gewünschte
Grenzfrequenz fgu hängt vom Verwendungszweck des Verstärkers ab; bei einem
Telefonie-Verstärker liegt sie bei 300 Hz, für einen HiFi-Verstärker wird man 20 Hz
fordern.
Nun definieren sowohl Tc1 wie auch Tc3 je eine untere Grenzfrequenz. Für die
Wahl der Eckfrequenzen Tc1 und Tc3 gibt es verschiedene Möglichkeiten. Man
könnte z.B. Tc1 = Tc3 setzen; damit hätte man aber bei dieser Frequenz eine Dämpfung von 6 dB gegenüber dem Durchlassbereich, die Grenzfrequenz würde also
höher liegen. Eine andere Möglichkeit wäre, dass entweder Tc1 oder Tc3 die Grenzfrequenz definiert; die andere Eckfrequenz müsste dann um mindestens eine
Dekade tiefer gelegt werden, damit der Amplitudengang bei der Grenzfrequenz
nicht beeinflusst wird. Als Entscheidungshilfe sollen einmal die beiden Eckfrequenzen genauer betrachtet werden:
I CA
1
1
ω c1 = ---------------- ≈ ---------------- = -------------------------β ⋅ U T ⋅ C1
r ein C 1 r BE C 1
ICA
ω c3 ≈ ------------------UT ⋅ CE
Man erkennt, dass Tc1 noch vom einer starken Exemplarstreuung unterworfenen
Stromverstärkungsfaktor $ abhängig ist, Tc3 hingegen ist nur von Elementwerten
und Arbeitspunktgrössen abhängig, ist also wesentlich genauer definiert (auch
wenn CE als Elektrolyt-Kondensator eine grössere Toleranz aufweist). Sinnvollerweise lässt man also die untere Grenzfrequenz des Verstärkers durch die Eckfrequenz Tc3 definieren und wählt Tc1 um einen Faktor von mindestens 10 kleiner. Die
Eckfrequenz Tc2 ist damit ja automatisch bestimmt.
Ein weiteres Argument, das für diese Wahl spricht, ist die Tatsache, dass CE in
jedem Fall einiges grösser sein wird als C1. In den meisten Fällen wird CE ein Elektrolyt-Kondensator sein, bei dem Volumen und Preis etwa proportional mit dem
Kapazitätswert wachsen. Bei den üblicherweise für C1 verwendeten Folien- oder
gar Keramik-Kondensatoren sind Preis und Baugrösse nur wenig von der Kapazität
abhängig. Aus diesem Grund muss man die Eckfrequenzen so legen, dass die Schaltung platzsparend und kostengünstig realisiert werden kann: CE muss so klein wie
möglich sein, also muss Tc3 die Grenzfrequenz festlegen.
44
Der Transistor als Verstärker
Das führt auf die folgenden Dimensionierungsgleichungen:
I CA
C E = --------------------ω gu ⋅ U T
10 ⋅ ICA
C 1 = -------------------------------------β min ⋅ ω gu ⋅ U T
Der resultierende Frequenzgang weist dann etwa den in der Abbildung 6.38
skizzierten Verlauf auf:
U3/U1
0dB
ωc2
ωc1
ωc3 = ωgu
ω
Abb. 6.38: Resultierender Amplitudengang (nur Asymptoten)
Als Zahlenbeispiel diene die Schaltung von Abbildung 177; anhand der dort
angegebenen Elementwerte sollen die wesentlichen Eckfrequenzen berechnet und
nachher durch Messungen (bzw. durch Simulationen1) nachgeprüft werden.
1. Auf dem Markt sind einige Programme erhältlich, die eine bequeme Simulation von elektronischen Schaltungen erlauben. Praktisch alle Programme beruhen auf SPICE (Simulation
Programm with Integrated Circuits Emphasis), einem Programm, das anfangs der 70er
Jahre an der Berkeley University entwickelt wurde. SPICE arbeitet mit ziemlich genauen
Modellen für die Halbleiter, so dass Simulationsresultate recht zuverlässig sind. Eine Simulation kann aber niemals den Experimentieraufbau mit realen Bauelementen vollständig
ersetzen, da z.B. das Layout der Schaltung und andere parasitäre Effekte nicht erfasst werden können.
Verbreitete Programme sind PSpice (Design Center von OrCAD), IS-SPICE von Intusoft,
Electronics Workbench oder das im Beispiel verwendete TINA von DesignSoft sind
Beispiele für PC-basierende Programme.
6.4 Die Emitterschaltung
45
18V
22kΩ
3.9kΩ
2N2219A
680nF
u1
8.2kΩ
2.2kΩ
u2
3.3µF
Abb. 6.39: Dimensionierte Schaltung
Für den Kollektorstrom ICA erhält man nach kurzer Rechnung etwa 2 mA. Daraus
folgt für die Eckfrequenz Tc3 = 23'300 s-1 (fc3 = fgu = 3700 Hz); für die Eckfrequenz fc1 erwartet man einen Wert, der je nach Stromverstärkung des Transistors
zwischen 40 Hz und 180 Hz liegt. Die letzte, an sich bedeutungslose Eckfrequenz
fc2 liegt bei den gegebenen Werten bei etwa 22 Hz.
Abb. 6.40: Simulierter Amplitudengang
Das Beispiel zeigt eine gute Übereinstimmung zwischen den berechneten Eckfrequenzen und dem simulierten Amplitudengang, mindestens was die dominante
Eckfrequenz (bzw. Grenzfrequenz) betrifft.
46
Der Transistor als Verstärker
Die in diesem Abschnitt gewonnenen Resultate gelten nur für die hier betrachtete
Schaltung und können nicht ohne weiteres auf andere Verstärkerstufen übertragen
werden. Die Methodik des Rechnungsganges ist aber bei allen Frequenzganguntersuchungen die gleiche.
6.5
Die Kollektorschaltung
Die Transistor-Grundschaltungen werden nach derjenigen Transistor-Elektrode
benannt, die dem Ein- und Ausgangskreis gemeinsam ist. Bei der Emitterschaltung
ist es der Emitter, der mindestens signalmässig am Masse liegt, also Ein- und Ausgang gemeinsam ist. Bei der Kollektorschaltung müsste dies folgerichtig der
Kollektor sein. Die Basis ist die Eingangsklemme, der Emitter ist die Ausgangsklemme (siehe Abbildung 6.41). Man erkennt sofort, dass wegen der in erster
Näherung konstanten Basis-Emitter-Spannung die Spannungsverstärkung gleich
Eins sein muss (ohne Phasendrehung); man nennt deshalb die Schaltung auch Emitterfolger, weil der Emitter der Basis folgt.
Eine Spannungsverstärkung von Eins ist nicht gerade spektakulär, die Schaltung
muss offenbar interessante Eigenschaften haben, was Ein- und Ausgangswiderstand
betrifft. In den folgenden Überlegungen und Berechnungen soll deshalb auf diese
Widerstände ein besonderes Augenmerk gerichtet werden.
6.5.1
Kenngrössen der Kollektorschaltung
Zur Berechnung der Kenngrössen des Emitterfolgers gehen wir von der vollständigen Schaltung mit Arbeitspunkteinstellung aus (Abbildung 6.41).
UCC
R1
RQ
C1
u0
u1
R2
UEA
RE
Abb. 6.41: Kollektorschaltung (Emitterfolger)
u2
6.5 Die Kollektorschaltung
47
Aus später ersichtlichen Gründen wurde in diesem Schema die Signalquelle mit
ihrem Innenwiderstand RQ mit eingezeichnet. Zunächst soll die Spannungsverstärkung u2/u1 berechnet werden; als Grundlage dazu dient die Kleinsignalersatzschaltung (Abbildung 6.42):
RQ
rBE
iB
βiB
u0
u1
Rp
rCE
RE
u2
Abb. 6.42: KSE des Emitterfolgers
Durch Zusammenfassen der Widerstände rCE und RE erhält man die vereinfachte
Ersatzschaltung von Abbildung 6.43:
RQ
rBE
iB
β iB
u0
u1
Rp
R’E
u2
Abb. 6.43: Vereinfachte KSE
Mit Hilfe dieser Ersatzschaltung lassen sich Ein- und Ausgangsspannung leicht
berechnen:
u 1 = i B ⋅ r BE + ( 1 + β ) ⋅ R' E ⋅ i B
u 2 = i B ⋅ ( 1 + β ) ⋅ R' E
Daraus erhält man für die gesuchte Spannungsverstärkung:
48
Der Transistor als Verstärker
( 1 + β )R' E
u
r BE
1
-----2 = ---------------------------------------- = ----------------------------------- ≈ 1 – ------------------------u1
r BE + ( 1 + β )R' E
( 1 + β )R' E
r BE
1 + -------------------------( 1 + β )R'E
U T ⎛ r CE + RE⎞
UT
≈ 1 – --------------------- = 1 – -------------------- ⎜ ----------------------⎟
I CA ⋅ R'E
I CA ⋅ R E ⎝ r CE ⎠
Für das Schlussresultat erhält man durch Einsetzen der bekannten Beziehung für
rCE und der Arbeitspunktgrössen:
u2
UT ⎛
U EA⎞
----- ≈ 1 – ---------- ⎜ 1 + ----------⎟ ≈ 1
u1
U EA ⎝
UK ⎠
Setzt man für das Emitter-Ruhepotential UEA einige Volt ein, so erkennt man sofort,
dass die Spannungsverstärkung innerhalb der erreichbaren Messgenauigkeit gleich
Eins ist.
Was nun den Eingangswiderstand angeht, so erkennt man bei Betrachtung der
Ersatzschaltung (Abbildung 6.43), dass der Basisspannungsteiler Rp parallel zu
einem “inneren” Eingangswiderstand u1/iB liegt. Für den resultierenden Eingangswiderstand folgt also:
⎛ u 1⎞
r ein = Rp || ⎜ -----⎟ = R p || ( r BE + ( 1 + β ) ⋅ R E ) ≈ R p || β ⋅ R E
⎝ iB⎠
Bevor dieses Resultat weiterdiskutiert wird, soll zuerst noch der Ausgangswiderstand des Emitterfolgers berechnet werden. Für diese Rechnung nimmt man für die
Signalspannung u0 = 0 an und erhält dann die angepasste Ersatzschaltung (Abbildung 6.44):
6.5 Die Kollektorschaltung
rBE
iB
49
i2
βiB
RQ
Rp
R’E
u2
Abb. 6.44: Ersatzschaltung zur Berechnung des Ausgangswiderstandes
Mit R’Q = Rp || RQ und analogen Überlegungen wie bei der Berechnung des Eingangswiderstandes erhält man für den Ausgangswiderstand raus:
u2
r BE + R' Q
⎛ U T R'Q⎞
||
||
||
-----------------------------------------------= R'E
≈ R'E ⎜ --------- + --------⎟
r aus = R'E
(1 + β)
iB ⋅ ( 1 + β )
β ⎠
⎝ I CA
Die bisher berechneten Kenngrössen sollen anhand eines Zahlenbeispiels auch
numerisch abgeschätzt werden. Den Rechnungen liegen die folgenden Werte
zugrunde: R1 = R2 = 56 kS, RE = 5.6 kS, RQ = 1 kS, $ = 100, UCC = 12 V. Damit
wird UEA . 5.4 V und ICA . 1 mA; weiter gilt: rBE . 2600 S. Der Widerstand rCE
wird bei diesen Rechnungen vernachlässigt. Man erhält für Ein- und Ausgangswiderstand die folgenden Werte:
r ein ≈ R p || ( r BE + ( 1 + β )R E ) = 28kΩ || ( 2.6kΩ + 100 ⋅ 5.6kΩ )
= 28kΩ || 562.6kΩ
⎛ U T R p || R Q⎞
28kΩ || 1kΩ
r aus ≈ R E || ⎜ --------- + -------------------⎟ = 5.6kΩ || ⎛ 26Ω + ------------------------------⎞
⎝
⎠
β ⎠
100
⎝ I CA
≈ 5.6kΩ || 36Ω
Aus diesen Zahlwerten erkennt man, dass insbesondere der relativ hohe innere Eingangswiderstand durch den Basisspannungsteiler praktisch “kurzgeschlossen”
wird. Der Ausgangswiderstand ist hingegen sehr klein, RE spielt dabei fast keine
Rolle mehr. Der Emitterfolger dient als Impedanzwandler (hoher Eingangswiderstand und kleiner Ausgangswiderstand). Man findet deshalb Emitterfolger meistens
als Ausgangsstufen von Verstärkern.
50
Der Transistor als Verstärker
Da bei einem solchen Verstärker die einzelnen Stufen ohnehin einen stabilen
Arbeitspunkt aufweisen müssen, kann der Emitterfolger ohne eigenen
Basisspannungsteiler an die letzte Stufe direkt angeschlossen werden (Abbildung
6.45):
UCC
RC
RE
Abb. 6.45: Direkt gekoppelter Emitterfolger als Ausgangsstufe
In dieser für einen Emitterfolger typischen Schaltung entfällt also der Basisspannungsteiler und die Ausdrücke für Ein- und Ausgangswiderstand können etwas
modifiziert werden:
rein ≈ r BE + ( 1 + β ) ⋅ RE ≈ β ⋅ R E
⎛ U T R Q⎞ U T RQ
||
r aus ≈ R E ⎜ --------- + -------⎟ ≈ --------- + ------⎝ I CA β ⎠ ICA β
In einem weiten Bereich ist also der Eingangswiderstand gleich dem mit $ multiplizierten Lastwiderstand RE und der Ausgangswiderstand wird im wesentlichen
durch den durch $ geteilten Quellwiderstand RQ (RQ = Ausgangswiderstand der
vorhergehenden Stufe) bestimmt. Um die relativ komplizierte Abhängigkeit des
Ausgangswiderstandes vom Quellwiderstand zu illustrieren, kann man Ausgangsund Quellwiderstand auf RE normieren. Für eine Stromverstärkung $ = 100 und
UEA = 6 V erhält man dann den Verlauf von Abbildung 6.46.
6.5 Die Kollektorschaltung
51
1
raus/RE
10-1
10-2
10-3 -3
10
10-2
10-1
1
101
102
103
104
RQ/RE
Abb. 6.46: Abhängigkeit des Ausgangswiderstandes vom Quellenwiderstand
In einem weiten Bereich ist der Ausgangswiderstand massgebend durch den Quellwiderstand RQ bestimmt; begrenzend wirken nach unten der Widerstand UT/ICA
und nach oben RE. Bei der Kollektorschaltung sieht man quasi durch die Schaltung
hindurch (Eingangswiderstand ist abhängig vom Lastwiderstand, Ausgangswiderstand ist abhängig vom Quellwiderstand), man sagt deshalb auch, der Emitterfolger
sei transparent.
6.5.2
Schwingneigung des Emitterfolgers
Im Gegensatz zu den bisher betrachteten Schaltungen zeigt der Emitterfolger
besonders bei kapazitiver Belastung (z.B. die Eingangskapazität des Oszilloskops
ohne Tastkopf) eine ausgeprägte Schwingneigung, d.h. er produziert selbständig
Schwingungen. Zur Erklärung dieses Phänomens muss die Ersatzschaltung des
Transistors noch weiter verfeinert werden. Durch Einführung der beiden Kondensatoren CCB und CBE erhält man die auch für mittlere Frequenzen taugliche
Ersatzschaltung von Abbildung 6.47:
iB
CCB
iR
uBE
CBE
rBE
iC
β0iR
rCE
uCE
Abb. 6.47: Transistor-Ersatzschaltung für mittlere Frequenzen
52
Der Transistor als Verstärker
Die neu eingeführten Kapazitäten sind einerseits die Sperrschichtkapazität CCB der
Kollektor-Basis-Diode, die nur wenige pF beträgt, sowie die wesentlich grössere
Diffusionskapazität CBE der leitenden Basis-Emitter-Diode. Diese Diffusionskapazität CBE ist einigermassen linear proportional zum Basis-Ruhestrom IBA und
kann bis zu einigen Hundert pF betragen. Man beachte, dass der Steuerstrom iR der
gesteuerten Stromquelle nicht mehr mit dem gesamten Basisstrom iB identisch ist!
Um den Einfluss der beiden Kondensatoren abzuschätzen, kann man die Transistorgleichungen (Vierpol-Gleichungen in Hybrid-Schreibweise) anhand dieser
Ersatzschaltung berechnen und mit den Gleichungen für die einfache Ersatzschaltung vergleichen. Nach längeren Rechnungen erhält man für die Transistorgleichungen:
r BE
jωr BE C CB
u BE = i B ⋅ ---------------------------------------------------------- + u CE ⋅ ---------------------------------------------------------1 + jωr BE ( C BE + C CB )
1 + jωr BE ( C BE + C CB )
jωβ0 C CB
β0
⎛ 1
⎞
i C = i B ⋅ ---------------------------------------------------------- + u CE ⋅ ⎜ --------- + ----------------------------------------------------------⎟
1 + jωr BE ( C BE + C CB )
⎝ r CE 1 + jωr BE ( C BE + C CB )⎠
Die Transistorparameter werden nun alle komplex; am stärksten wirkt sich dabei
die Frequenzabhängigkeit der Stromverstärkung $ aus. Die Frequenzabhängigkeit
der übrigen Transistor-Parameter soll für die folgenden Überlegungen der Einfachheit halber vernachlässigt werden. Die nachfolgenden Rechnungen sind deshalb
auch nur als relativ grobe Näherungen aufzufassen.
Für $ kann man schreiben: $(T) = $(T) / n(T) . Diese Frequenzabhängigkeit kann
durch den Frequenzgang der Stromverstärkung (Abbildung 6.48) dargestellt werden. Wie bereits erwähnt, ist CBE >> CCB, also folgt für die Eckfrequenz Tc des
Frequenzganges:
1
1
1
ω c = ------------------------------------------ ≈ -------------------- = --r BE ( C BE + C CB ) r BE C BE
τ
Da nun aber die Diffusionskapazität CBE etwa proportional, rBE hingegen umgekehrt proportional zum Basis-Ruhestrom IBA ist, wird diese Eckfrequenz ziemlich
unabhängig vom Arbeitspunkt. Da der Amplitudengang mit 1 Dekade/Dekade
sinkt, geht er bei der Frequenz TT = $0 Tc durch 1 (0 dB). Die Frequenz fT = TT/2B
wird Transitfrequenz des Transistors genannt und ist eine im Datenblatt angegebene Kenngrösse.
6.5 Die Kollektorschaltung
53
103
β β0
102
101
1
10-1
103
104
105
106
107
108
fT
109
f/Hz
0°
ϕ
-90°
Abb. 6.48: Frequenzgang der Stromverstärkung $
Beim Transistor 2N2219A beträgt die Transitfrequenz fT etwa 250 MHz; für die
Abbildung 6.48 wurde eine Gleichstromverstärkung $0 = 300 angenommen. Man
beachte, dass bei der Frequenz fc = fT/$0 der Betrag der Stromverstärkung nur etwa
70% von $0 beträgt und dass zwischen Basisstrom und Kollektorstrom eine Phasenverschiebung von 45° besteht. Ausgehend von diesen Beziehungen kann die Zeitkonstante J = 1/Tc leicht berechnet werden:
54
Der Transistor als Verstärker
β0
1
τ = ------ = ------ωT
ωc
Betrachten wir nun den Eingangskreis eines kapazitiv belasteten Emitterfolgers,
wobei noch eine Zuleitungsinduktivität L in den Quellenkreis eingefügt wurde
(Abbildung 6.49):
RQ
RQ
L
Zein
L
RS
CE
RE
-jXS
Abb. 6.49: Eingangskreis eines kapazitiv belasteten Emitterfolgers
Die Eingangsimpedanz des Emitterfolgers wurde dabei durch eine SerieErsatzschaltung RS - jXS erfasst. Unter der realistischen Annahme, dass die beiden
Zeitkonstanten rBECBE und RECE etwa gleich gross ( = J) seien, folgt für die
Eingangsimpedanz des Emitterfolgers:
β0 ⋅ RE
β0 ⋅ RE
Z ein ≈ β ⋅ Z E = -------------------------- = --------------------------------------------2
2 2
( 1 – ω τ ) + j2ωτ
( 1 + jωτ )
2 2
β 0 ⋅ R E ( 1 – ω τ ) – jω2τβ 0 R E
= ---------------------------------------------------------------------------- = R S – jXS
2 2 2
2 2
( 1 – ω τ ) + ω 4τ
2 2
β0 ⋅ RE ( 1 – ω τ )
ω2τβ 0 R E
= --------------------------------------------------- – j ⋅ --------------------------------------------------2 2 2
2 2
2 2 2
2 2
( 1 – ω τ ) + ω 4τ
( 1 – ω τ ) + ω 4τ
Die auf $0RE normierte Resistanz bzw. die normierte Reaktanz der Eingangsimpedanz zeigen die folgenden Frequenzabhängigkeiten:
6.5 Die Kollektorschaltung
55
1.0
RS / β0RE 0.8
0.6
0.4
0.2
0
-0.2
0.01
0.1
1
10
100
ωτ
Abb. 6.50: Normierter Realteil der Eingangsimpedanz
0.8
XS / β0RE
0.6
0.4
0.2
0
0.01
0.1
1
10
100
ωτ
Abb. 6.51: Verlauf von Xs (normierte Reaktanz)
Eine alternative Darstellung ist die Ortskurve der Eingangsimpedanz mit der Frequenz als Parameter:
Im{Zein}
β 0 RE
Abb. 6.52: Ortskurve der Eingangsimpedanz
Re{Zein}
56
Der Transistor als Verstärker
Man erkennt, dass bei gewissen Frequenzen der Realteil der Eingangsimpedanz
negativ wird. Falls die Resonanzfrequenz (definiert durch L und XS) in diesem Frequenzgebiet liegt und gleichzeitig der resultierende Widerstand im Kreis (RQ + RS)
# 0 ist, so liegt ein verlustloser oder gar entdämpfter Serie-Resonanzkreis vor, der
eine Schwingung mit seiner Resonanzfrequenz produziert. Eine solche Schwingung
kann verhindert werden, wenn durch einen passenden Vorwiderstand RV dafür
gesorgt wird, dass bei den in Frage kommenden Frequenzen der resultierende
Kreiswiderstand positiv wird (Abbildung 6.53):
UCC
R1
RV
C1
R2
RE
CE
Abb. 6.53: Stabiler Emitterfolger
Die Grösse von RV muss meistens durch Versuche ermittelt werden; man sollte den
Widerstand so gross wie nötig und so klein wie möglich machen.
6.5.3
Emitterfolger mit kapazitiv angekoppelter Last
In vielen Fällen ist der Emitterwiderstand RE gleichzeitig der Lastwiderstand.
Gewisse Lasten (z.B. ein Kopfhörer) ertragen aber keinen Gleichstrom (unerwünschte Vormagnetisierung) und müssen deshalb kapazitiv angekoppelt werden.
Dieser Fall muss nun genau untersucht werden (Abbildung 6.54).
Berechnen wir zunächst den Strom IR:
U E = U EA + u L
⇒
U EA u L
I R = ----------- + ------R E RE
Für den Strom IE im Emitteranschluss gilt gemäss Knotensatz (der Kondensator C
wird dabei als Kurzschluss für Signale betrachtet):
6.5 Die Kollektorschaltung
57
UCC
IE
UE
C
IR
iL
RE
RL
uL
Abb. 6.54: Emitterfolger mit kapazitiv angekoppelter Last
U EA u L u L
I E = IR + i L = ----------- + ------- + -----RE RE RL
Bedingt durch den pn-Übergang (Basis-Emitter-Diode) kann dieser Strom nie negativ werden. Der kritische Fall liegt dann vor, wenn gilt uL = - ûL. Für diesen Fall
erhalten wir die folgende Ungleichung:
U EA û L û L
---------- – ------- – ------ ≥ 0
RE RE RL
Diese Ungleichung kann nun nach den verschiedenen Parametern aufgelöst werden;
es resultieren daraus die folgenden vier Ungleichungen, die für die Dimensionierung verwendet werden können:
R E⎞
⎛
U EA ≥ û L ⎜ 1 + -------⎟
R L⎠
⎝
RL
û L ≤ U EA ⋅ -------------------RE + RL
⎛ U EA
⎞
R E ≤ R L ⎜ ----------- – 1⎟
⎝ û L
⎠
û L
---------------------RL ≥ RE ⋅
U EA – û L
58
Der Transistor als Verstärker
Wenn diese Ungleichungen nicht erfüllt sind, resultieren erhebliche Verzerrungen
des Ausgangssignals. Machen wir noch ein Zahlenbeispiel dazu: als Last diene ein
Kopfhörer mit einem Widerstand von 200 S, die Amplitude der Ausgangsspannung
ûL soll 4.5 V betragen (50 mW Ausgangsleistung). Die Spannung UEA betrage 6 V.
Wie gross muss der Widerstand RE gewählt werden ? Aus den obigen Ungleichungen kann man entnehmen:
⎛ U EA ⎞
6V
R E ≤ RL ⎜ ----------- – 1⎟ = 200Ω ⋅ ⎛ ----------- – 1⎞ = 66.7Ω
⎝ 4.5V
⎠
⎝ û L
⎠
Der Emitterwiderstand muss also recht klein gewählt werden. Falls man
RE = 100 S wählt, ergibt sich für die maximale Amplitude der Ausgangsspannung:
RL
200Ω
û L ≤ U EA ⋅ -------------------- = 6V ⋅ ---------------------------------- = 4V
RE + RL
100Ω + 200Ω
Leistung und Wirkungsgrad
Die gesamte von der Verstärkerstufe aufgenommene Leistung ist gleich dem
Produkt aus Quellenspannung UCC und Kollektor- bzw. Emitterstrom des Transistors. Für den Momentanwert der aufgenommenen Leistung erhalten wir unter der
Voraussetzung harmonischer Signale:
û L
⎛ U EA û L
⎞
p T ( t ) = U CC ⋅ ⎜ ----------- + ------- ⋅ sin ( ωt ) + ------ ⋅ sin ( ωt )⎟
RL
⎝ RE RE
⎠
Für den Mittelwert der aufgenommenen Leistung erhalten wir einfach:
U CC ⋅ U EA
P T = --------------------------RE
Die vom Emitterfolger abgegebene Nutzleistung pN(t) ist gegeben durch:
2
2
2
û L ⋅ ( sin ( ωt ) )
û L
p N ( t ) = ------------------------------------- = ---------- ⋅ ( 1 – cos ( 2ωt ) )
RL
2R L
6.5 Die Kollektorschaltung
59
Für den Mittelwert dieser Leistung erhalten wir:
2
û L
P N = ---------2R L
Der Wirkungsgrad 0 der Schaltung ist wie üblich definiert als Verhältnis von
abgegebener Leistung (Nutzleistung) zur gesamten aufgenommenen Leistung. Es
gilt also:
2
RE
PN
û L
--------------------------------------η =
=
⋅
PT
2R L U CC ⋅ U EA
Es dürfte sicher sinnvoll sein, wenn wir die Schaltung so dimensionieren, dass der
Wirkungsgrad maximal wird. Dabei sind aber noch einige Nebenbedingungen zu
beachten. Auf Grund unserer vorherigen Überlegungen haben wir für den Widerstand RE die folgende Einschränkung gefunden:
⎛ U EA
⎞
R E ≤ R L ⋅ ⎜ ----------- – 1⎟
⎝ û L
⎠
Je grösser das Verhältnis UEA/ûL wird, desto grösser kann RE gewählt werden und
desto grösser wird folglich auch der Wirkungsgrad. Anderseits muss aus Gründen
der Aussteuerbarkeit auch die folgende Ungleichung erfüllt sein:
U EA ≤ U CC – û L
Im Interesse eines optimalen Wirkungsgrades wählen wir UEA so gross wie
möglich, also UEA = UCC - ûL. Aus denselben Gründen wird auch der zulässige
Maximalwert von RE gewählt:
⎛ U EA
⎞
⎛ U CC – û L
⎞
⎛ U CC ⎞
R E = R L ⋅ ⎜ ----------- – 1⎟ = RL ⋅ ⎜ ----------------------- – 1⎟ = R L ⋅ ⎜ ----------- – 2⎟
û L
⎝ û L
⎠
⎝
⎠
⎝ û L
⎠
Damit die Beziehungen leichter interpretierbar werden, normieren wir die
Amplitude der Ausgangsspannung auf die halbe Betriebsspannung, machen also
den folgenden Ansatz:
U CC
û L = α ⋅ ----------2
0≤α≤1
60
Der Transistor als Verstärker
Unter Verwendung der normierten Amplitude " erhalten wir für den Widerstand
RE:
1
1–α
R E = 2R L ⎛ --- – 1⎞ = 2R L ⋅ -----------⎝α ⎠
α
Für das optimale Emitterruhepotential erhalten wir demnach:
U CC
U CC
α
U EA = U CC – α ⋅ ----------- = U CC ⎛ 1 – ---⎞ = ----------- ( 2 – α )
⎝
2
2
2⎠
Setzen wir all das in die Beziehung für den Wirkungsgrad ein, so erhalten wir nach
einigen Zwischenrechnungen:
α( 1 – α)
η = --------------------2( 2 – α )
Wir stellen fest, dass der Wirkungsgrad dieser Schaltung bei optimaler
Dimensionierung nur noch von der normierten Amplitude " abhängig ist. Diese
Abhängigkeit ist in Abbildung 6.55 grafisch dargestellt.
10%
η
5%
0%
0
0.5
α
Abb. 6.55: Verlauf des Wirkungsgrades
1
6.5 Die Kollektorschaltung
61
Eine genaue Analyse zeigt, dass für " = 0.5858 . 0.6 der Wirkungsgrad 0 seinen
maximalen Wert von 0.0858 = 8.58% erreicht. Das Maximum ist aber relativ flach,
so dass bei nur kleinen Einbussen an Wirkungsgrad die Amplitude der Ausgangsspannung in relativ grossen Grenzen verändert werden kann. Wenn wir beispielsweise ein Absinken des Wirkungsgrades auf 8% zulassen, so darf die normierte
Amplitude " in einem Bereich von 0.46 # " # 0.70 liegen. Die Anforderungen an
die Genauigkeit der Realisierung sind also nicht sehr hoch.
Machen wir dazu ein Beispiel. Die Amplitude der Ausgangsspannung soll ûL = 5 V
betragen bei einem Lastwiderstand von RL = 50 S. Wenn wir " = 0.66 wählen,
also einen Wirkungsgrad von immer noch mehr als 8% erreichen, so folgt für die
Betriebsspannung ein Wert von UCC = 15 V. Das Emitterruhepotential muss bei
UEA = 10 V liegen. Für den Emitterwiderstand RE erhalten wir schliesslich einen
Wert von RE = 50 S.
Insgesamt gesehen hat diese Art von gleichstromfreier Ausgangsstufe einen
miserablen Wirkungsgrad; wir werden uns deshalb später noch mit besser
geeigneten Ausgangs-Schaltungen beschäftigen müssen.
Anmerkung
Die in diesem Kapitel besprochenen einfachen Schaltungen haben in dieser Form in
der heutigen Elektronik keine grosse Bedeutung mehr. Es geht deshalb im ganzen
Kapitel primär um die Anwendung von Verfahren (z. B. um das Konzept der Kleinsignal-Ersatzschaltung) und um die Methoden zur Analyse und Optimierung von
Schaltungen. Diese Erkenntnisse können dann auch auf kompliziertere Schaltungen
übertragen werden.
62
Der Transistor als Verstärker
6.6
Übungsaufgaben und Kontrollfragen
6.6.1
Übungsaufgaben
18.
Analysiere die Arbeitspunktgrössen in der folgenden Schaltung:
+12V
39k
3k3
12k
1k5
Abb. 6.56: Schaltung zu Aufgabe 18
In welchen Grenzen schwankt der Kollektor-Ruhestrom ICA in dieser
Schaltung
unter
folgenden
Annahmen
(genaue
Rechnung):
$min = 50 @ 20°C, $max 6 4, 0°C # h # 80°C, UBE = 0.62 V @ 20
19.
Gesucht wird die Kennlinie U = f(I) des nachfolgenden Zweipols.
Fallunterscheidung: Transistor leitend bzw. gesperrt.
R1
I
U
R2
Abb. 6.57: Zweipol von Aufgabe 19
20.
Berechne das Kollektor-Ruhepotential UCA dieser Schaltung:
UCC
R1
R2
RC
UCA
Abb. 6.58: Schaltung zu Aufgabe 20
6.6 Übungsaufgaben und Kontrollfragen
21.
63
Man berechne die Kollektor-Ruheströme der beiden Transistoren unter den
Voraussetzungen UBE = konstant = 0.6 V und $1 = $2 6 4.
+12 V
4.7 kΩ
T2
T1
15 kΩ
3.3 kΩ
220 Ω
390 Ω
Abb. 6.59: Schaltung zu Aufgabe 21
22.
In der folgenden Schaltung steht C2 für eine parasitäre Lastkapazität, z.B.
ein an den Ausgang angeschlossenes Koaxialkabel oder ein KO-Eingang.
Für die Rechnung darf rCE vernachlässigt werden.
R1
RC
C2
C1
u1
R2
RE
u2
Abb. 6.60: Schaltung zu Aufgabe 22
a) Berechne die Spannungsverstärkung u2/u1 sowie den Eingangswiderstand dieser Schaltung.
b) Skizziere der Frequenzgang (Amplituden- und Phasengang) der Schaltung unter Angabe der Eckfrequenzen.
23.
Berechne Spannungsverstärkung sowie Ein- und Ausgangswiderstand der
folgenden Schaltung (Abbildung 6.61); rCE darf auch hier vernachlässigt
werden. Vergleiche die erhaltenen Resultate mit denen der klassischen
Emitterschaltung (mit Basis-Spannungsteiler).
64
Der Transistor als Verstärker
UCC
RC
R1
C
R2
Abb. 6.61: Schaltung zu Aufgabe 23
24.
Bootstrap-Schaltung
C1
R1
RB
CE
R2
RE
Abb. 6.62: Bootstrap-Schaltung (Aufgabe 24)
a) Versuche unter Verwendung des einfachen Transistor-Modells (Kap. 4)
diese Schaltung zu verstehen und ihre Eigenschaften zu beschreiben.
b) Berechne den genauen Eingangswiderstand unter Verwendung der vollständigen Kleinsignal-Ersatzschaltung.
c) Welchen Einfluss hat der Kondensator CE auf den Eingangswiderstand ?
25.
Berechne alle wichtigen Verstärkerparameter (Spannungsverstärkung, Eingangswiderstand und Ausgangswiderstand) der nachfolgenden Schaltung
(Abbildung 6.63), die auch unter dem Namen „Basis-Schaltung“ bekannt
ist.
6.6 Übungsaufgaben und Kontrollfragen
R1
RC
R2
RE
65
C1
CB
Abb. 6.63: Basis-Schaltung (zu Aufgabe 25)
26.
Berechne den Frequenzgang dieser Verstärkerstufe. Die Kondensatoren C1
und CE sollen dabei als Kurzschlüsse für Signale betrachtet werden; rCE
darf vernachlässigt werden. Welchen Einfluss hat CCB?
R1
CCB
RC
C1
R2
RE
CE
Abb. 6.64: Schaltung zu Aufgabe 26
27.
Analysiere die folgende sogenannte Kaskode-Schaltung.
R1
RC
T2
C1
R2
T1
CB
R3 RE
CE
Abb. 6.65: Kaskode-Schaltung (zu Aufgabe 27)
66
Der Transistor als Verstärker
a) Berechne die Spannungsverstärkung dieser Schaltung.
b) Wie würde sich in dieser Schaltung ein Kondensator zwischen Kollektor
und Basis von T1 auswirken? Hinweis: Berechne die Spannungsverstärkung
von Eingang zum Kollektor von T1.
6.6.2
Fragen zur Lernkontrolle
Es wird erwartet, dass die folgenden Fragen ohne im Buch nachzuschlagen beantwortet werden können.
1.
Weshalb ist eine Arbeitspunkteinstellung mit konstanter Basis-EmitterSpannung praktisch nicht brauchbar?
2.
Wie hängt die Stromverstärkung $ von der Temperatur ab?
3.
Wozu benötigt man eigentlich Arbeitspunkt- oder Ruhegrössen?
4.
Welches sind die wichtigsten Grössen, die die Stabilität eines
Arbeitspunktes beeinflussen?
5.
Wie lautet die Faustregel zur Dimensionierung des Basis-Spannungsteilers?
6.
Was versteht man unter der Dynamik eines Verstärkers?
7.
Welche Grundidee liegt der Kleinsignal-Ersatzschaltung zugrunde?
8.
In welcher Grössenordnung liegt die Early-Spannung UK?
9.
Wie ist der Klirrfaktor eines Verstärkers definiert?
10.
Wie kann die Schwingneigung eines kapazitiv belasteten Emitterfolgers
bekämpft werden?
11.
Wie lassen sich rBE und rCE ausdrücken?