Eulersche Zahl - kraibacher.com
Werbung

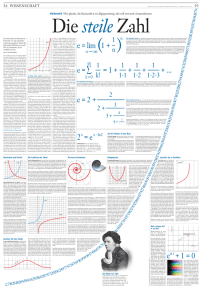
Eulersche Zahl aus Wikipedia, der freien Enzyklopädie Die eulersche Zahl = 2,71828 18284 59045 23536 02874 71352 66249 77572 47093 69995 … (Folge A001113 in OEIS), benannt nach dem Schweizer Mathematiker Leonhard Euler, ist eine irrationale und sogar transzendente reelle Zahl. Sie ist die Basis des natürlichen Logarithmus und der (natürlichen) Exponentialfunktion. Diese (spezielle) Exponentialfunktion wird aufgrund dieser Beziehung zur Zahl häufig kurz -Funktion genannt. Die eulersche Zahl spielt in der gesamten Analysis und allen damit verbundenen Teilgebieten der Mathematik und besonders in der Differential- und Integralrechnung eine zentrale Rolle. Sie gehört zu den wichtigsten Konstanten der Mathematik.[1] Inhaltsverzeichnis 1 2 3 4 5 6 Definition Herkunft des Symbols e Eigenschaften Weitere Darstellungen für die eulersche Zahl Kettenbruchentwicklungen Anschauliche Interpretationen der eulerschen Zahl 6.1 Zinseszinsrechnung 6.2 Wahrscheinlichkeitsrechnung 7 Charakterisierung der eulerschen Zahl nach Steiner 8 Bruchnäherungen 9 Berechnung der Nachkommastellen 9.1 Entwicklung der Anzahl der bekannten Nachkommastellen von e 10 Literatur 11 Weblinks 12 Einzelnachweise und Fußnoten Definition Unter der Zahl Für ist nach Leonhard Euler der Grenzwert der folgenden unendlichen Reihe zu verstehen:[2] ist dabei definiert ist. die Fakultät von , also im Falle Wie schon Euler bewies, erhält man die eulersche Zahl das Produkt der natürlichen Zahlen von bis , während ebenfalls als funktionalen Grenzwert:[3] , was insbesondere bedeutet, dass er sich auch beim Grenzübergang der Folge ergibt: . Dem liegt zugrunde, dass gilt, also nichts weiter ist als der Funktionswert der Exponentialfunktion[4] an der Stelle . Die obige Reihendarstellung von ergibt sich in diesem Zusammenhang dadurch, dass man die Taylorreihe der Exponentialfunktion um die Entwicklungsstelle an der Stelle auswertet. Ein alternativer Zugang zur Definition der eulerschen Zahl ist derjenige über Intervallschachtelungen, etwa in der Weise, wie es in Theorie und Anwendung der unendlichen Reihen von Konrad Knopp dargestellt wird. Danach gilt:[5] Herkunft des Symbols e Als frühestes Dokument, welches die Verwendung des Buchstabens für diese Zahl durch Leonhard Euler aufweist, gilt ein Brief Eulers an Christian Goldbach vom 25. November 1731. Als nächste gesicherte Quelle für die Verwendung dieses Buchstabens gilt Eulers Werk Mechanica sive motus scientia analytice exposita, II aus dem Jahre 1736.[6] In der im Jahre 1748 erschienenen Introductio in Analysin Infinitorum greift Euler diese Bezeichnung wieder auf.[7] Es gibt keine Hinweise, dass diese Wahl des Buchstabens in Anlehnung an seinen Namen geschah. Unklar ist auch, ob er dies in Anlehnung an die Exponentialfunktion oder aus praktischen Erwägungen der Abgrenzung zu den viel benutzten Buchstaben a, b, c oder d machte. Obwohl auch andere Bezeichnungen in Gebrauch waren, etwa c in d’Alemberts Histoire de l’Académie, hat sich durchgesetzt. Eigenschaften Die eulersche Zahl ist eine transzendente (Beweis nach Charles Hermite, 1873) und damit irrationale Zahl (Beweis). Sie lässt sich also (wie auch die Kreiszahl nach Ferdinand von Lindemann 1882) weder als Bruch zweier natürlicher Zahlen noch als Lösung einer algebraischen Gleichung endlichen Grades darstellen und besitzt folglich eine unendliche nichtperiodische Dezimalbruchentwicklung. Das Irrationalitätsmaß von ist 2 und somit so klein wie möglich für eine irrationale Zahl, insbesondere ist nicht liouvillesch. Es ist nicht bekannt, ob zu irgendeiner Basis normal ist.[8] In der eulerschen Identität werden fundamentale mathematische Konstanten in Zusammenhang gesetzt: Die ganze Zahl 1, die eulersche Zahl , die imaginäre Einheit der komplexen Zahlen und die Kreiszahl . Die eulersche Zahl ist die durch eindeutig bestimmte positive reelle Zahl . Sie tritt auch in der asymptotischen Abschätzung der Fakultät auf (siehe Stirlingformel):[9] Weitere Darstellungen für die eulersche Zahl Die eulersche Zahl lässt sich auch durch oder durch den Grenzwert des Quotienten aus Fakultät und Subfakultät beschreiben: Eine Verbindung zur Verteilung der Primzahlen wird über die Formeln deutlich, wobei die Primzahlfunktion und das Symbol das Primorial der Zahl bedeutet. Auch eher von exotischem Reiz als von praktischer Bedeutung ist die catalansche Darstellung Kettenbruchentwicklungen Im Zusammenhang mit der Zahl gibt es spätestens seit dem Erscheinen von Leonhard Eulers Introductio in Analysin Infinitorum im Jahre 1748 eine große Anzahl Kettenbruchentwicklungen für und aus ableitbare Größen. So hat Euler die folgende klassische Identität für gefunden: Die Identität (1) weist offenbar ein regelmäßiges Muster auf, das sich bis ins Unendliche fortsetzt. Sie gibt einen regulären Kettenbruch wieder, der von Euler aus dem folgenden abgeleitet wurde:[10] Letzterer Kettenbruch ist seinerseits ein Spezialfall des folgenden mit : Eine andere klassische Kettenbruchentwicklung, die jedoch nicht regelmäßig ist, stammt ebenfalls von Euler:[11] [12] Auf Euler und Ernesto Cesàro geht eine weitere Kettenbruchentwicklung der eulerschen Zahl zurück, die von anderem Muster als in (1) ist: [13] Im Zusammenhang mit der eulerschen Zahl existiert darüber hinaus eine große Anzahl von allgemeinen kettenbruchtheoretischen Funktionalgleichungen. So nennt Oskar Perron als eine von mehreren die folgende allgemein gültige Darstellung der -Funktion:[14] Ein weiteres Beispiel hierfür ist die von Johann Heinrich Lambert stammende Entwicklung des Tangens Hyperbolicus, die zu den lambertschen Kettenbrüchen gerechnet wird:[15][16] Anschauliche Interpretationen der eulerschen Zahl Zinseszinsrechnung Das folgende Beispiel macht die Berechnung der eulerschen Zahl nicht nur anschaulicher, sondern es beschreibt auch die Geschichte der Entdeckung der eulerschen Zahl: Ihre ersten Stellen wurden von Jakob Bernoulli bei der Untersuchung der Zinseszinsrechnung gefunden. Den Grenzwert der ersten Formel kann man folgendermaßen deuten: Jemand zahlt am 1. Januar einen Euro auf der Bank ein. Die Bank garantiert ihm eine momentane Verzinsung zu einem Zinssatz pro Jahr. Wie groß ist sein Guthaben am 1. Januar des nächsten Jahres, wenn er die Zinsen zu gleichen Bedingungen anlegt? Nach der Zinseszinsformel wird aus dem Startkapital In diesem Beispiel sind und Jahr erfolgt, also bei unterjähriger Verzinsung. nach Verzinsungen mit Zinssatz das Kapital , wenn der Zinszuschlag jährlich erfolgt, oder , wenn der Zinszuschlag -mal im Bei jährlichem Zuschlag wäre Bei halbjährlichem Zuschlag hat man , also schon etwas mehr. Bei täglicher Verzinsung ( Wenn man momentan verzinst, wird ) erhält man unendlich groß, und man bekommt die oben angegebene erste Formel für . Wahrscheinlichkeitsrechnung ist auch häufig in der Wahrscheinlichkeitstheorie anzutreffen: Beispielsweise sei angenommen, dass ein Bäcker für jedes Brötchen eine Rosine in den Teig gibt und diesen gut durchknetet. Danach enthält statistisch gesehen jedes -te Brötchen keine Rosine. Die Wahrscheinlichkeit , dass bei Brötchen keine der Rosinen in einem fest gewählten ist, ergibt im Grenzwert für (37%-Regel): Charakterisierung der eulerschen Zahl nach Steiner Im vierzigsten Band von Crelles Journal aus dem Jahre 1850 gibt der Schweizer Mathematiker Jakob Steiner eine Charakterisierung der eulerschen Zahl , wonach als Lösung einer Extremwertaufgabe verstanden werden kann. Steiner zeigte nämlich, dass die Zahl charakterisierbar ist als diejenige eindeutig bestimmte positive reelle Zahl, die beim Wurzelziehen mit sich selbst die größte Wurzel liefert. Wörtlich schreibt Steiner: „Wird jede Zahl durch sich selbst radicirt, so gewährt die Zahl e die allergrößte Wurzel.“[17] Steiner behandelt hier die Frage, ob für die Funktion das globale Maximum existiert und wie es zu bestimmen ist. Seine Aussage ist, dass es existiert und dass es angenommen wird in und nur in . In seinem Buch Triumph der Mathematik gibt Heinrich Dörrie eine elementare Lösung dieser Extremwertaufgabe. Sein Ansatz geht von der folgenden wahren Aussage über die reelle Exponentialfunktion aus: Nach der Substitution folgt für alle reellen Zahlen mittels einfacher Umformungen weiter und schließlich für alle positiven durch Radizieren [18][19] Bruchnäherungen Für die Zahl und daraus abgeleitete Größen gibt es verschiedene näherungsweise Darstellungen mittels Brüchen. So fand Charles Hermite die folgenden Bruchnäherungen: Hier weicht der erstgenannte Bruch um weniger als 0,0003 Prozent von ab.[20] Die optimale Bruchnäherung im dreistelligen Zahlenbereich, also die optimale Bruchnäherung mit , ist .[21] Diese Näherung ist jedoch nicht die beste Bruchnäherung im Sinne der Forderung, dass der Nenner höchstens dreistellig sein soll. Die in diesem Sinne beste Bruchnäherung ergibt sich als 9. Näherungsbruch der Kettenbruchentwicklung der eulerschen Zahl: Aus den Näherungsbrüchen der zu gehörenden Kettenbruchentwicklungen (s. o.) ergeben sich Bruchnäherungen beliebiger Genauigkeit für und daraus abgeleitete Größen. Mit diesen findet man sehr effizient beste Bruchnäherungen der eulerschen Zahl in beliebigen Zahlenbereichen. So erhält etwa im fünfstelligen Zahlenbereich die beste Bruchnäherung , die zeigt, dass die von Charles Hermite für die eulersche Zahl im fünfstelligen Zahlenbereich gefundene Bruchnäherung noch nicht optimal war. In gleicher Weise hat etwa C. D. Olds gezeigt, dass durch die Näherung für die eulersche Zahl eine weitere Verbesserung, nämlich , zu erzielen ist.[22] Insgesamt beginnt die Folge der besten Näherungsbrüche der eulerschen Zahl, welche sich aus ihrer regelmäßigen Kettenbruchdarstellung ergeben, folgendermaßen:[23] Berechnung der Nachkommastellen Zur Berechnung der Nachkommastellen wird meist die Reihendarstellung ausgewertet, die schnell konvergiert. Wichtig bei der Implementierung ist dabei Langzahlarithmetik, damit die Rundungsfehler nicht das Ergebnis verfälschen. Ein Verfahren, das ebenfalls auf dieser Formel beruht, aber ohne aufwendige Implementierung auskommt, ist der Tröpfelalgorithmus zur Berechnung der Nachkommastellen von , den A. H. J. Sale fand.[24] Entwicklung der Anzahl der bekannten Nachkommastellen von e Datum Anzahl 1748 Mathematiker 23 Leonhard Euler[25] 1853 137 William Shanks 1871 205 William Shanks 1884 346 J. Marcus Boorman 1946 1949 808 ? 2.010 John von Neumann (berechnet auf dem ENIAC) 1961 100.265 Daniel Shanks und John Wrench 1981 116.000 Steve Wozniak (berechnet mithilfe eines Apple II) 1994 Mai 1997 August 1997 September 1997 Februar 1999 Oktober 1999 21. November 1999 10.000.000 Robert Nemiroff und Jerry Bonnell 18.199.978 Patrick Demichel 20.000.000 Birger Seifert 50.000.817 Patrick Demichel 200.000.579 Sebastian Wedeniwski 869.894.101 Sebastian Wedeniwski 1.250.000.000 Xavier Gourdon 10. Juli 2000 2.147.483.648 Shigeru Kondo und Xavier Gourdon 16. Juli 2000 3.221.225.472 Colin Martin und Xavier Gourdon 2. August 2000 6.442.450.944 Shigeru Kondo und Xavier Gourdon 16. August 2000 12.884.901.000 Shigeru Kondo und Xavier Gourdon 21. August 2003 25.100.000.000 Shigeru Kondo und Xavier Gourdon 18. September 2003 50.100.000.000 Shigeru Kondo und Xavier Gourdon 27. April 2007 100.000.000.000 Shigeru Kondo und Steve Pagliarulo 6. Mai 2009 200.000.000.000 Shigeru Kondo und Steve Pagliarulo 20. Februar 2010 500.000.000.000 Alexander Yee[26] 5. Juli 2010 1.000.000.000.000 Shigeru Kondo[26] Literatur Brian J. McCartin: e: The Master of All. Mathematical Intelligencer, Band 28, 2006, Nr. 2, S. 10–21. Der Artikel erhielt den ChauvenetPreis. Online. (http://mathdl.maa.org/mathDL/22/?pa=content&sa=viewDocument&nodeId=3368) Heinrich Dörrie: Triumph der Mathematik. Hundert berühmte Probleme aus zwei Jahrtausenden mathematischer Kultur. 5. Auflage. Physica-Verlag, Würzburg 1958. Leonhard Euler: Einleitung in die Analysis des Unendlichen. Erster Teil der Introductio in Analysin Infinitorum (Reprint der Ausgabe Berlin 1885). Springer Verlag, Berlin – Heidelberg – New York 1983, ISBN 3-540-12218-4. MR0715928 (http://ams.math.unibielefeld.de/mathscinet/search/publdoc.html? arg3=&co4=AND&co5=AND&co6=AND&co7=AND&dr=all&pg4=AUCN&pg5=TI&pg6=PC&pg7=ALLF&pg8=ET&review_format=html&s4=Euler%2C% pid=715928) Konrad Knopp: Theorie und Anwendung der unendlichen Reihen (= Die Grundlehren der Mathematischen Wissenschaften. 2). 5., berichtigte Auflage. Springer Verlag, Berlin/ Göttingen/ Heidelberg/ New York 1964, ISBN 3-540-03138-3. MR0183997 (http://ams.math.uni-bielefeld.de/mathscinet/search/publdoc.html? arg3=&co4=AND&co5=AND&co6=AND&co7=AND&dr=all&pg4=AUCN&pg5=TI&pg6=PC&pg7=ALLF&pg8=ET&review_format=html&s4=Knopp%2C pid=183997) Eli Maor: e: the Story of a Number. Princeton University Press, Princeton 1994, ISBN 978-0-691-14134-3. Eli Maor: Die Zahl e: Geschichte und Geschichten. Birkhäuser Verlag, Basel (u. a.) 1996, ISBN 3-7643-5093-8. C. D. Olds: The simple continued fraction expansion of e. In: American_Mathematical_Monthly. 77, 1971, S. 968-974. Oskar Perron: Irrationalzahlen. Nachdruck der 2., durchgesehenen Auflage (Berlin, 1939). 4. durchgesehene und ergänzte Auflage. Walter de Gruyter Verlag, Berlin 2011, ISBN 978-3-11-083604-2, doi:10.1515/9783110836042.fm (http://dx.doi.org/10.1515%2F9783110836042.fm). Oskar Perron: Die Lehre von den Kettenbrüchen - Band II: Analytisch-funktionentheoretische Kettenbrüche. Reprografischer Nachdruck der dritten, verbesserten und durchgesehenen Auflage, Stuttgart 1957. 4. durchgesehene und ergänzte Auflage. Teubner Verlag, Stuttgart 1977, ISBN 3-519-02022-X. J. Steiner: Über das größte Product der Theile oder Summanden jeder Zahl. In: Journal für die reine und angewandte Mathematik. 40, 1850, S. 208 (Online (http://gdz.sub.uni-goettingen.de/dms/load/img/?PPN=PPN243919689_0040&DMDID=DMDLOG_0028)). David Wells: Das Lexikon der Zahlen. Aus dem Englischen von Dr. Klaus Volkert. Originaltitel: The Penguin Dictionary of Curious and Interesting Numbers. Fischer Taschenbuch Verlag, Frankfurt/Main 1990, ISBN 3-596-10135-2. Weblinks Commons: Eulersche Zahl (https://commons.wikimedia.org/wiki/Category:E_(mathematical_constant)?uselang=de) – Sammlung von Bildern, Videos und Audiodateien Wiktionary: eulersche Zahl – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen Eric W. Weisstein: e (http://mathworld.wolfram.com/e.html). In: MathWorld (englisch). Intuitiv verständliche Verbildlichung von e in einem interaktiven Java-Applet (http://www.matheonline.at/galerie/log/n_EulerscheZahl.html) Verständliche Erklärung und Herleitung der eulerschen Zahl (http://matheguru.com/19-die-zahl-e.html) e auf eine Million Stellen bei Project Gutenberg (http://www.gutenberg.org/etext/127) (englisch) Ausführliche Informationen und Angaben zu relevanter Literatur (http://numbers.computation.free.fr/Constants/E/e.html) (englisch) Einzelnachweise und Fußnoten 1. Man beachte: Die eulersche Zahl ist nicht identisch mit der Euler-Mascheroni-Konstante , welche in manchen Quellen den ähnlich klingenden Namen eulersche Konstante hat. 2. Euler: Einleitung … (§ 122). S. 226–227. 3. Euler: Einleitung … (§§ 123,125). S. 91-94. 4. oder auch „ -Funktion“ 5. Knopp: Theorie und Anwendung… (§ 9). S. 84. 6. Knopp a.a.O.: 7. Euler: Einleitung … (§ 122). S. 91. Euler schreibt (gemäß der Übersetzung von Hermann Maser) dazu: Wir werden nun in der Folge der Kürze wegen für diese Zahl stets den Buchstaben gebrauchen, so dass also die Basis der natürlichen oder hyperbolischen Logarithmen bedeutet, […] , oder es soll stets die Summe der unendlichen Reihe bezeichnen. 8. Richard George Stoneham: A general arithmetic construction of transcendental non-Liouville normal numbers from rational fractions. (http://matwbn.icm.edu.pl/ksiazki/aa/aa16/aa1632.pdf) (PDF-Datei, 692 kB), Acta Arithmetica 16, 1970, S. 239–253. 9. Die Stirling-Formel. (http://www.staff.uni-mainz.de/pommeren/Kryptologie/Klassisch/1_Monoalph/Stirling.pdf) (PDF-Datei; 78 kB), James Stirling: Methodus Differentialis, 1730, S. 1. 10. Perron: Irrationalzahlen. S. 115. 11. Euler: S. 305. 12. Folge A073333 in OEIS 13. Perron: Die Lehre von den Kettenbrüchen - Band II. S. 19. 14. Perron: Die Lehre von den Kettenbrüchen - Band II a. a. O.. 15. Perron: Die Lehre von den Kettenbrüchen - Band II. S. 157. 16. Man beachte die Verbindung zu Identität (3)! 17. In: Journal für die reine und angewandte Mathematik. 40, S. 208. 18. Dörrie: S. 358. 19. Man kann diese Aufgabe auch mit den bei der Kurvendiskussion in der Differentialrechnung angewandten Methoden lösen. 20. Maor: S. 185. 21. Wells: S. 46. 22. Olds: In: Amer. Math. Monthly. S. 973. 23. Siehe: Folge A007676 in OEIS (Zähler) / Folge A0A007677 in OEIS (Nenner) 24. A. H. J. Sale: The calculation of e to many significant digits. The Computer Journal, Vol. 11 (2), 1986. S. 229–230. (online (http://comjnl.oxfordjournals.org/content/11/2/229.abstract)) 25. Leonhardo Eulero: Introductio in analysin infinitorum Band 1, Marcus-Michaelis Bousquet und socii, Lausannæ 1748, (lateinisch; „2,71828182845904523536028“ auf S. 90 (http://books.google.de/books?id=jQ1bAAAAQAAJ&pg=PA90)) 26. http://numberworld.org/digits/E/ Von „http://de.wikipedia.org/w/index.php?title=Eulersche_Zahl&oldid=141762164“ Kategorien: Analysis Besondere Zahl Folgen und Reihen Diese Seite wurde zuletzt am 4. Mai 2015 um 14:54 Uhr geändert. Abrufstatistik Der Text ist unter der Lizenz „Creative Commons Attribution/Share Alike“ verfügbar; Informationen zu den Urhebern und zum Lizenzstatus eingebundener Mediendateien (etwa Bilder oder Videos) können im Regelfall durch Anklicken dieser abgerufen werden. Möglicherweise unterliegen die Inhalte jeweils zusätzlichen Bedingungen. Durch die Nutzung dieser Website erklären Sie sich mit den Nutzungsbedingungen und der Datenschutzrichtlinie einverstanden. Wikipedia® ist eine eingetragene Marke der Wikimedia Foundation Inc.