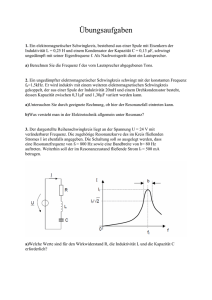
E 12 „Gedämpfter Schwingkreis“

Fakultät für Physik und Geowissenschaften
Physikalisches Grundpraktikum
E 12 „Gedämpfter Schwingkreis“
Aufgaben
1. Messen Sie die frequenzabhängige Stromaufnahme eines RLC-Serienresonanzkreises für drei verschiedene Dämpfungswiderstände Rd.
2. Zeichnen Sie die Resonanzkurven und bestimmen Sie aus den Halbwertsbreiten die jeweiligen Dämpfungskonstanten δ* und Güten Q des Schwingkreises. Vergleichen Sie die Werte von δ* mit den aus
Rσ/2L berechneten Werten. Fitten Sie die theoretische Funktion an die gemessenen Resonanzkurven
und bestimmen Sie daraus f0 und δ*. Ermitteln Sie die Kapazität des Kondensators mit der ThomsonGleichung.
3. Messen Sie die frequenzabhängige Stromaufnahme eines Schaltkreises, in dem Kapazität C und Induktivität L parallel und in Reihe zum Widerstand R geschaltet sind. Leiten Sie einen Ausdruck für die
Impedanz dieses Schaltkreises her, erklären Sie die Beobachtungen und fitten Sie die theoretische Kurve
an die gemessenen Daten. Vergleichen Sie die Resonanzfrequenz mit dem in Aufgabe 2 erhaltenen
Wert.
Zusatzaufgabe. Untersuchen Sie den Einfluss eines zum Kondensator parallel geschalteten Widerstandes RC auf die Resonanzfrequenz. Dazu ist die Resonanzfrequenz mittels der Phasenverschiebungsmessung in Abhängigkeit von RC zu messen und grafisch darzustellen. Tragen Sie in das Diagramm die berechenbaren Werte ein und diskutieren Sie den Kurvenverlauf.
Literatur
Physikalisches Praktikum, 13. Auflage, Hrsg. W. Schenk, F. Kremer, Elektrizitätslehre, 3.0.1, 3.0.2, 3.03,
4.02
Gerthsen Physik, D. Meschede, 22. Auflage, 7.6.3, 7.6.7
Zubehör
Funktionsgenerator, Digitalmultimeter, Messschaltung, Zweikanal-Oszilloskop
Schwerpunkte zur Vorbereitung
 Induktive, kapazitive und ohmsche Widerstände im Wechselstromkreis bzw. Serienschwingkreis
(komplexe Darstellung von Wechselstromgrößen, Zeigerdiagramme)
 ungedämpfte, gedämpfte und erzwungene Schwingungen, Eigenfrequenz, Resonanzfrequenz,
Reihen- und Parallelschwingkreis
 Schwingkreisgleichung, Resonanzkurve, Halbwertsbreite, Dämpfung, Güte
 Stromresonanz, Spannungsüberhöhung
 Frequenzabhängigkeit der Widerstände und des Phasenwinkels zwischen Strom und Spannung
 Ersatzschaltung für verlustbehaftete Induktivität bzw. Kapazität
 Messungen der Phasenbeziehungen zwischen Strom und Spannung (Lissajous-Figuren)
 Aufbau und Funktionsprinzip einer Elektronenstrahlröhre, Funktionseinheiten eines Oszilloskops
1
Bemerkungen zum Versuch
Die Betriebsspannung des Resonanzkreises U0 soll bei allen Frequenzen 0.4 V betragen und ist ggf. über
den Amplitudenregler des Generators nach der Änderung der Frequenz nachzuregeln. Der Messbereich
der Digitalmultimeter ist optimal zu wählen. Vor dem Einschalten des Generators müssen die Versuchsschaltungen durch die BetreuerInnen überprüft werden.
In diesem Versuch wird die Stromaufnahme des Resonanzkreises indirekt über den Spannungsabfall UR
am Dämpfungswiderstand Rd gemessen: I = UR/Rd, siehe Abb. 1. Dies schließt den Einfluss des Innenwiderstands des Amperemeters auf die Dämpfung aus. Eine exakte Messung der Resonanzfrequenz ist bei
Verwendung eines Oszilloskops über die Phasenverschiebung  zwischen Strom und Spannung
[(f0)=0)] möglich. Zur Aufnahme der Resonanzkurve ist ein Frequenzbereich unterhalb und oberhalb
der Resonanzfrequenz f0 zu wählen, so dass 0.2  UR(f)/UR(f0)  1. Die graphische Darstellung der Resonanzkurve erfolgt in einem Diagramm UR(f)/UR(f0) als Funktion der Frequenz f für alle drei Dämpfungswiderstände.
In Aufgabe 2 kann aus den Resonanzkurven bei den entsprechenden Punkten die Halbwertsbreite Δf
entnommen werden. Damit ist die Dämpfungskonstante δ* (δ*exp = π Δf) zu berechnen. Berechnen Sie
weiterhin die Dämpfungskonstante δ* mit der Gleichung δ*ber=Rσ/2L, wobei vorher die Induktivität L der
Spule mit einem Induktivitätsmessgerät (LC-Meter) gemessen wird. Rσ bezeichnet den gesamten Ohmschen Widerstand. Diskutieren Sie die Unterschiede zwischen den auf verschiedene Weise bestimmten
Dämpfungskonstanten unter Berücksichtigung der Messunsicherheiten. Da L bekannt ist, kann mit der
Resonanzfrequenz f0 unter Verwendung der Thomson-Gleichung auch die Kapazität des Kondensators
berechnet werden:
 0  2 f0 =
1
.
LC
Abb 1. Messschaltung RLC Serienkreis
G: Funktionsgenerator (Rigol)
Ch. I, Ch. II: Kanäle des Zweikanal-Oszilloskops
Rd: Dämpfungswiderstand
L: Induktivität der Spule
RSp: ohmscher Anteil der Spule
C: Kapazität des Kondensators
V(U0): Voltmeter Hameg 8012
U0: Spannung am Resonanzkreis
UR: Spannung am Widerstand
V(UR): Voltmeter Agilent 34450A
In Aufgabe 3 ist die Schaltung so abzuändern, dass Kondensator und Spule parallel geschaltet sind. Die
Resonanzkurve ist nur für einen Messwiderstand R aufzunehmen. Die Betriebsspannung des Resonanzkreises U0 sollte konstant gehalten werden und nicht mehr als 1 V betragen.
Abb 2. Messschaltung RLC Parallelkreis
G: Funktionsgenerator (Rigol)
Ch. I, Ch. II: Kanäle des Zweikanal-Oszilloskops
R: Messwiderstand
L: Induktivität der Spule
RSp: ohmscher Anteil der Spule
C: Kapazität des Kondensators
V(U0): Voltmeter Hameg 8012
U0: Spannung am Resonanzkreis
UR: Spannung am Messwiderstand
V(UR): Voltmeter Agilent 34450A

2
Grundlagen
Wichtige Gleichungen im Reihenschwingkreis
Scheitelwert des Stroms
Uˆ
Iˆ =
2
1 

R +  L 

C

2
σ
f 0 0 L

f R σ
Q=
Güte des Serienkreises Q:
L -
Phasenverschiebung 
tan  =
Resonanzüberhöhung
UL ( f0 )
U0
=
1
C
Rσ
UC ( f0 )
U0
=
1
Rσ
L 0 L
1
=
=
C
R
0R C
Die entsprechenden Gleichungen für den Parallelschwingkreis sind herzuleiten.
Serienschwingkreis mit verlustbehafteter Kapazität
(Komplexe Größen sind unterstrichen.)
In der Regel wird die frequenzabhängige Stromaufnahme I() eines Serienschwingkreises durch
I () 
U0
Z ()

U0


R  i  L 
1 
C 
(1a)
mit dem Betrag
I ( ) 
U0
2 1
 2 
1  2
Rσ   L 

C  


(1b)
dargestellt. In den Gln. (1a) und (1b) sind U0 die (konstante) Spannung am Schwingkreiseingang, L die
Induktivität und C die Kapazität des Kreises sowie =2f die Kreisfrequenz. Alle im Schwingkreis wirkenden reellen (ohmschen) Widerstände sind dabei in R additiv zusammengefasst, d. h. R=R+RL+RC*
(Dämpfungswiderstand R, Verlustwiderstände RL und RC* der Induktivität bzw. Kapazität). Dabei wird
meistens vorausgesetzt, dass diese Definition von R auf einem Ersatzschaltbild der realen Induktivität
bzw. Kapazität aus einem Blindwiderstand (iL bzw. -i/C) und einem in Reihe geschalteten Verlustwiderstand (RL bzw. RC*) basiert.
Für die Induktivität ist das physikalisch wegen der stromproportionalen Verluste, bedingt u. a. durch
den Ohmschen Widerstand des Spulendrahtes, sinnvoll. Für die Kapazität ist aber im Hinblick auf die
spannungsproportionalen Verluste als Folge der Polarisation im Dielektrikum eine Parallelschaltung von
verlustfreier Kapazität C und Verlustwiderstand RC zutreffender. Diese Schaltung zeigt in Übereinstimmung mit der Realität für einen Frequenzwert f = 0 den Verlustwiderstand RC und für f den Widerstand null. In Abb. 2 wird die vergleichende Analyse der beiden möglichen Ersatzschaltbilder der Kapazi-
3
tät mit den komplexen Widerständen RC(p) und RC(r) gezeigt.
a)
b)
Abb. 2 Ersatzschaltbilder der verlustbehafteten Kapazität
*
(a) R (r)
C ( )  R C 
1
iC
(b) RC(p) ( ) 
*
RC
1  iCCRC
(p)
Einer Ersatzschaltung nach Abb. 2b mit dem komplexen Widerstand RC kann eine Schaltung nach Abb.
2a in Abhängigkeit von C* und RC* jeweils nur für eine einzelne Frequenz i entsprechend der Gl. (2a)
vollständig äquivalent sein:
(r)
R (p)
C ( i )  R C ( i ) .
(2a)
Das erkennt man, wenn die aus dieser Gleichsetzung resultierenden Bedingungen berechnet werden,
unter denen Gl. (2a) gilt:
RC
1
RC* 
C*  C 
(2b)
2
1  (iRCC )
(iRC )2 C
Bei kleinen Verlusten [1/( 2RC2C 2) << 1 bzw. RC2 >> 1/( 2C2)] gilt die Näherung C*C.
Legt man nun aus den oben genannten Gründen der Berechnung des Serienresonanzkreises die physikalisch sinnvollere Ersatzschaltung der Kapazität nach Abb. 2b zugrunde, ergibt sich gegenüber dem in Gl.
(1a) stehenden komplexen Widerstand eine etwas veränderte Beziehung für die frequenzabhängige
Impedanz Z( ):









 1   
1

 1 
Z ( )  R  RL  
R  i  L  
2  C
2

 ( RCC )   

  1  C 
1    R C  


  C  


(3)
Der Unterschied zum Ansatz nach Gl. (1a) besteht in einer Frequenzabhängigkeit des Realteiles und in
einem Faktor (in den geschweiften Klammern) vor 1/C im Imaginärteil, der eine Abhängigkeit der Resonanzfrequenz von dem Verlustwiderstand RC zur Folge hat. Definiert man hier wie üblich 0 als die
Frequenz, für die der Imaginärteil verschwindet, so folgt aus Gl. (3)
 1  1 2 
0    
 
 LC  RC C  

L 
0  00 1  2 
 RC C 
1/2
mit
1/2
1
00   
 LC 
4
bzw.
(4a)
1/2
.
(4b)
Mit dieser Resonanzfrequenz ergibt sich für den reellen Resonanzwiderstand des Kreises aus Gl. (3)
Z (0 )  R  RL 
1 L
.
RC C
(5a)
Dieses Ergebnis liefert auf direktem Wege die Grundlage dafür, wie man für 0, und nur in diesem Fall,
den Verlustwiderstand RC mit Hilfe des L/C-Verhältnisses zu den im Kreis wirkenden Ohmschen Widerstand additiv einbeziehen kann:
Z (0 )  R  RL  RC* ,
RC* 
1 L
RC C
.
(5b)
Die wesentliche Konsequenz der dargestellten Zusammenhänge besteht darin, dass Gl. (1) für alle Kreisfrequenzen   0 eine Näherung darstellt, die allerdings umso genauer ist, je größer RC im Vergleich zu
1/(C) ist und je weniger sich  von 0 unterscheidet.
Ergänzende Bemerkungen:
Bedeutsamer als die Unterschiede zwischen genäherter und tatsächlicher frequenzabhängiger Stromaufnahme des Kreises sind die Differenzen zwischen den (prinzipiell nicht messbaren) Spannungen an
einer idealen (verlustfreien) Induktivität (UL') und einer idealen Kapazität (UC') sowie den direkt messbaren Werten UL und UC an den verlustbehafteten Bauelementen. Gemäß Gl. (1b) gilt im Resonanzfall
UL' (00 )  UC' (00 )  U0
00L
Rσ
'
ULC
(00 )  0

U0
L
Rσ
C
und
.
(6a)
(6b)
ULC' ist die an der Reihenschaltung von verlustfreier Induktivität und verlustfreier Kapazität auftretende
Spannung. Die Berechnung der an den realen Bauelementen im Resonanzfall auftretenden Spannungen
UL(0), UC (0), ULC (0) und deren Beträge auf der Grundlage von Gl. (5a) liefert dagegen unter Berücksichtigung von Gl. (4b) (0  00) die Gleichungen (7) bis (9):
UL (0 )  Ior RL  i (RC RC*  RC*2 )1/2  ,
L

UL (0 )  Ior RL 2  RC*2  
C

(7a)
1/2
,
(7b)
UC (0 )  Ior RC* - i(RC RC*  RC*2 )1/2  ,
(8a)
1/2
L

C 
UC (0 )  Ior 

ULC (0 )  Ior 
RC
 1  i 0 RC C

 RL  i0 L 
,
(8b)
,
(9a)

ULC (0 )  Ior (RL  RC* ) .
Dabei ist Ior die Resonanzstromamplitude mit
5
(9b)
Ior 
U0
R  RL 
.
1 L
(10)
RC C
Im Gegensatz zu den „idealisierten“ Berechnungen nach den Gln. (6a) und (6b) zeigen die modifizierten
Gleichungen u.a., dass die Phasen der an den verlustbehafteten Bauelementen auftretenden, direkt
messbaren Spannungen im Resonanzfall etwas weniger als ± /2 gegenüber der Phase der angelegten
Spannung verschoben und die Beträge der Spannungen nicht exakt gleichgroß sind. Deshalb ist die an
der Reihenschaltung von Induktivität und Kapazität beobachtete Spannung ULC (0) ungleich null.
Die Gln. (7b), (8b) und (9b) bieten die Möglichkeit, den durch die Verlustanteile der Bauelemente und
den durch die Größe des Dämpfungswiderstandes R bedingten Anteil an der Schwingungsdämpfung
durch Messungen bei der Resonanzfrequenz analytisch zu ermitteln.
6