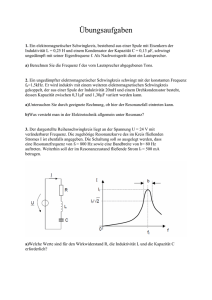
1.5.4. Selbstinduktion, Induktivität, Feldenergie Beim Einschalten

1.5.4. Selbstinduktion, Induktivität, Feldenergie
Beim Einschalten laut Schaltplan stellt man
fest, dass L1 kurz nach L2 zu leuchten beginnt.
In der Spule wird eine Spannung induziert, die
der Ursache ihrer Entstehung entgegenwirkt.
Daher leuchtet L1 später auf.
Die Selbstinduktionsspannung ergibt sich aus
dem Induktionsgesetz mit
∆B
U = −n ⋅ A ⋅
∆t
n⋅I
Setzt man für die Feldstärke B = µ 0 ⋅ µ r ⋅
ein, so erhält man
l
n⋅I 

∆ µ 0 ⋅ µ r ⋅

l 

.
U = −n ⋅ A ⋅
∆t
Die Stromstärke ist die einzige Größe, die sich zeitlich ändert. Daher kann man schreiben
n 2 ⋅ A ∆I
U = −µ 0 ⋅ µ r ⋅
.
⋅
l
∆t
Den Faktor µ 0 ⋅ µ r ⋅
n2 ⋅ A
bezeichnet man als Induktivität der Spule.
l
Physikalische Größe: Induktivität
Formelzeichen: L
Einheit: ein Henry (1 H)
n2 ⋅ A
Gleichung: L = µ 0 ⋅ µ r ⋅
l
Damit ist U = − L ⋅
∆I
∆t
Fließt durch die Spule einer Induktivität L der Strom I, so speichert sie die magnetische
1
Feldenergie W = ⋅ L ⋅ I 2
2
Eine quadratische Spule (l = 20 cm, Kantenlänge 5 cm) hat 1000 Windungen und einen
Eisenkern (mr = 300). Wie groß ist die Induktivität der Spule?
ges:
geg:
L
l = 20 cm = 0,2 m
a = 5 cm = 0,05 m à A = 0,0025 m2
n = 1000
mr = 300
m0 = 1,257 · 10–6 V · s · A–1 · m–1
Physik 12 GK
1
Gym 9
L = µ0 ⋅ µr ⋅
Lösung:
n2 ⋅ A
l
L = 1,257 ⋅ 10 −6 VsA −1 m −1 ⋅ 300 ⋅
1000 2 ⋅ 0,0025m 2
0,2m
Vs
A
L = 4,7 H
L = 4,7
Die Spule hat eine Induktivität von 4,7 H. Bei einer Stromstärkeänderung von 1 A in 1 s wird
also eine Spannung von 4,7 V induziert.
Physik 12 GK
2
Gym 9