Übungen zur Physik für Chemiker II

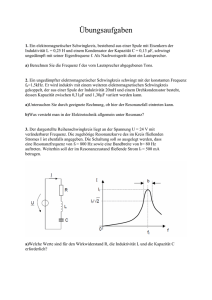
Übungen zur Vorlesung
Physik II - Elektromagnetismus
Dr. R. Mitdank, J. Boy, M. Kockert
Aufgaben zur 13. Übung am 18.07.17
Wechselstrom
49. Effektivwert
Ein elektrischer Verbraucher mit einem Widerstand von R = 100 Ω wird an einen Wechselspannungsgenerator angeschlossen, der
a) eine Dreieckspannung mit der Amplitude Uo = ±150 V und
b) eine Rechteckspannung mit dem Betrag Uo = ±150 V erzeugt.
Welche Leistung P wird jeweils im Verbraucher umgesetzt und welchen Betrag haben jeweils
die Effektivwerte von Stromstärke Ieff und Spannung Ueff?
50. R, L und C im Wechselstromkreis
An eine Wechselspannungsquelle (Ueff = 12 V; f = 50 Hz) werden nacheinander 1.) ein Kondensator, 2.) eine Spule und 3.) beide in Reihe angeschlossen. Die dabei gemessenen Effektivstromstärken betragen in dieser Reihenfolge I1 = 86 mA, I2 = 26 mA und I3 = 37 mA. Welche Beträge haben
a) die Kapazität C des Kondensators,
b) die Induktivität L und der ohmsche Widerstand R der Spule?
51. Maxwellbrücke
Mit Hilfe der in der Abbildung dargestellten
Messbrücke kann die Induktivität L einer
Spule einschließlich ihres Widerstandes R3
ermittelt werden. Bei anliegender Wechselspannung werden der Widerstand R2 und die
Kapazität C des Kondensators so eingestellt,
dass durch das Amperemeter kein Strom
fließt.
Welchen Betrag haben L und R3 einer „Eisenspule“, wenn R2 = 85 kΩ und C = 2,7 µF gemessen werden?
Es sei R1 = 300 Ω und R4 = 500 Ω.
52. Parallelresonanz zur Blindstromkompensation
Einer Spule der Induktivität L = 0,132 H mit einem Wirkwiderstand von R = 47,2 Ω wird ein
Kondensator C parallelgeschaltet. Bei Erregung durch die Spannung U(t) = Uoexp(iωt) und
der Frequenz f = 50 Hz soll die Phasenverschiebung zwischen der Spannung U(t) und dem
Strom I(t) = Ioexp[i(ωt-ϕ)] verschwinden. Berechnen Sie die Kapazität C des Phasenschieberkondensators.