B F B F
Werbung
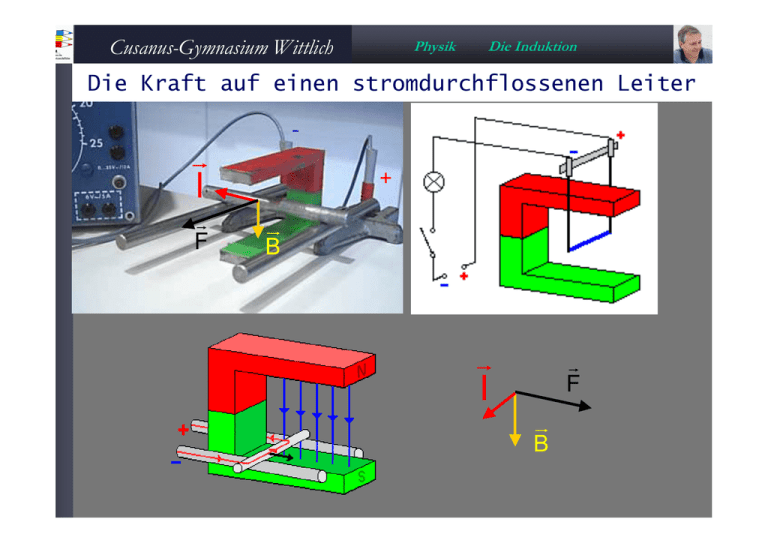
Cusanus-Gymnasium Wittlich Physik Die Induktion Die Kraft auf einen stromdurchflossenen Leiter - I F + B I F B Cusanus-Gymnasium Wittlich Physik Grundversuch 1 zur Induktion Die Induktion lat: inductio -Einführung Bewegt man einen Magneten (ein Magnetfeld) relativ zu einer Spule (zu einem Leiter), dann wird an den Enden der Spule (des Leiters) eine Spannung erzeugt (induziert)! Cusanus-Gymnasium Wittlich Physik Grundversuch 2 zur Induktion Die Induktion lat: inductio -Einführung Bewegt man einen Leiter relativ zu einem Magnetfeld, dann wird an den Enden des Leiters eine Spannung induziert! I v B Cusanus-Gymnasium Wittlich Der Generator Physik Die Induktion Cusanus-Gymnasium Wittlich Der Generator Physik Die Induktion Cusanus-Gymnasium Wittlich Physik Die Induktion Die sinusförmige Wechselspannung Cusanus-Gymnasium Wittlich Die Idee zum Elektromotor Physik 1 Die Induktion Cusanus-Gymnasium Wittlich Physik Die Idee zum Elektromotor Die Induktion 2 Statt der Kompassnadel bauen wir eine drehbar gelagerte stromdurchflossene Spule (also einen Elektromagneten) ein. Cusanus-Gymnasium Wittlich Physik Die Idee zum Elektromotor Die Induktion 3 Jetzt lassen wir den Strom mit abwechselnder Richtung durch die Spule fließen. Cusanus-Gymnasium Wittlich Physik Die Idee zum Elektromotor 4 + 1 + Die Induktion (Der Polwender) + 1 2 2 - + -- Cusanus-Gymnasium Wittlich Physik Die Induktion Der Gleichstromelektromotor Anker (Spule mit Kern) N S N Polwender Kohle- S schleifkontakte - + Cusanus-Gymnasium Wittlich Physik Die Induktion Gleichstromelektromotor -+ Durch den Polwender wird die Stromrichtung in der rotierenden Spule immer so gewählt, dass die Pole des Spulenmagnetfelds „richtig“ entstehen. Der Motor läuft in diesem Fall links herum. Cusanus-Gymnasium Wittlich Physik Die Induktion Gleichstromelektromotor Drehrichtung Stromrichtung Polwender F Spule Magnet I I B B F Cusanus-Gymnasium Wittlich Der Transformator Physik Die Induktion Cusanus-Gymnasium Wittlich Physik Die Induktion Der Transformator Up ∼ Us ∼ I-Kern (Joch) Primärspule U-Kern Sekundärspule Cusanus-Gymnasium Wittlich Physik Die Induktion Der unbelastete Transformator IP IS UP US nP Primärseite nP UP [V] 300 6 300 300 75 75 6 6 6 25 nS Sekundärseite nS US [V] 300 6 600 1200 1200 10000 12 24 96 3333 ! Cusanus-Gymnasium Wittlich Physik Die Induktion Der unbelastete Transformator IP IS UP US nP Primärseite nP UP [V] 300 100 600 1200 10000 75 100 100 100 150 nS Sekundärseite nS US [V] 300 100 300 300 1200 1 50 25 12 2 Cusanus-Gymnasium Wittlich Physik Die Induktion Der unbelastete Transformator IP IS UP US nP nS Spannungsverhältnisse am unbelasteten Transformator US nS = UP nP SpannungS WindungszahlS = SpannungP WindungszahlP Cusanus-Gymnasium Wittlich Physik Die Induktion Der Transformator US nS = UP nP US 12000 = 25 75 ⇒ US = 4000V Cusanus-Gymnasium Wittlich Physik Die Induktion Ströme am belasteten Transformator IP IS UP US Primärseite nP IP [A] 300 0,1 Sekundärseite nS IS [A] 300 0,1 600 1200 75 75 300 300 8 1 0,1 0,1 25 25 0,2 0,4 234 1875 Cusanus-Gymnasium Wittlich Physik Die Induktion Ströme am belasteten Transformator IP IS UP IP ns = IS np US StromstärkeP Windungszahls = StromstärkeS Windungszahlp Cusanus-Gymnasium Wittlich Physik Die Induktion Hochstrom-Transformator IP ns = IS np IP ⋅ nP 20A ⋅ 75 IS = = = 188A ns 8 Cusanus-Gymnasium Wittlich Physik Die Induktion Das Induktionsgesetz B t Ui = Ui (B,v,l) Vermutung : Ui ∼ B Ui ∼ v Ui ∼ l l v Ui s t + ∆t Cusanus-Gymnasium Wittlich Physik Die Induktion Das Induktionsgesetz Ui ∼ B Ui ∼ v Ui ∼ l Ui ∼ B ⋅ v ⋅ l Ui = B ⋅ v ⋅ l N m Nm [Ui ] = 1 Am ⋅ s ⋅ m = 1 As = 1V B t l v Ui s t + ∆t Cusanus-Gymnasium Wittlich Physik Die Induktion Das Induktionsgesetz Ui = B ⋅ v ⋅ l ∆s = B⋅ ⋅l ∆t ∆s ⋅ l = B⋅ ∆t ∆A = B⋅ ∆t B ∆A l v Ui t s t + ∆t Cusanus-Gymnasium Wittlich Physik Die Induktion Das Induktionsgesetz ∆A Ui = B ⋅ ∆t Für die momentane Induktionsspannung gilt damit: ∆A Ui (t) = lim (B ⋅ ) ∆t →0 ∆t i = B ⋅ A( t) B ∆A l v t s t + ∆t Ui Das Pr odukt Φ = B ⋅ A heißt Magnetischer Fluß Φ B = wird deswegenoft als Magnetische Flußdichte bezeichnet A dann gilt : • • • • Φ = B ⋅ A = B⋅ A + B ⋅ A Cusanus-Gymnasium Wittlich Physik Die Induktion Das Faradaysche Induktionsgesetz In einer Leiterschleife mit einer Win − dung wird eine Spannung induziert, wenn sich der magnetische Fluss in • Ui = Φ dieser Schleife verändert. • Ui = Φ Φ = B ⋅ A = B ⋅ A ⋅ cos α B 1791-1867 α A Der Flächenvektor A steht senkrecht auf der Fläche und hat einen Betrag der gerade dem Flächeninhalt von A entspricht. Cusanus-Gymnasium Wittlich Physik Die Induktion Das Faradaysche Induktionsgesetz In einer Spule mit n Windungen wird eine Spannung induziert, wenn sich der mag − • Ui = Φ netische Fluss in der Spule verändert. • Ui = −n ⋅ Φ Φ = B ⋅ A = B ⋅ A ⋅ cos α Hängt auch B von der Zeit ab, dann gilt : • • • • Φ = B ⋅ A = B⋅ A + B ⋅ A • 1791-1867 • Ui = − n i( B⋅ A + B ⋅ A ) Cusanus-Gymnasium Wittlich Physik Die Induktion Das Faradaysche Induktionsgesetz In einer Leiterschleife mit 1 Windung wird eine Spannung induziert, wenn sich der magnetische Fluss in dieser Schleife verändert. • Ui = Φ Φ = B ⋅ A = B ⋅ A ⋅ cosα Ui Durch die Bewegung des Magneten ändert sich der Fluss in der Leiterschleife mit der Fläche A. D.h. an den Enden entsteht eine Induktionsspannung Ui Wie ist diese Spannung gepolt? Cusanus-Gymnasium Wittlich Induktionsgesetz Physik Die Induktion - Lenzsche Regel Ui I Verbinde ich die beiden Enden der Leiterschleife, dann fließt in der Leiterschleife ein Strom I. Dieser Strom muss nun so gerichtet sein, dass das von ihm erzeugte Magnetfeld dem die Induktion erzeugenden Magnetfeld entgegengerichtet ist. dann gilt : • • • • Φ = B ⋅ A = B⋅ A + B ⋅ A Cusanus-Gymnasium Wittlich Induktionsgesetz - Physik Die Induktion Lenzsche Regel Cusanus-Gymnasium Wittlich Physik Die Induktion Versuch zur Lenzschen Regel V IRing BRing BSp + - ISp Lenz‘sche Regel: Eine induzierter Strom erzeugt immer ein Magnetfeld, das dem flusserzeugenden Magnetfeld entgegen gerichtet ist. Cusanus-Gymnasium Wittlich Physik Die Induktion Der Funkeninduktor Selbstunterbrecher Sekundärspule Primärspule n1 klein Eisenkern n2>100000 Cusanus-Gymnasium Wittlich Physik Die Induktion Die Selbstinduktion Einschaltvorgang: I und damit B ändern sich sehr schnell. • • I und damit B sind stark positiv. • • Ui = − n i( B⋅ A + B ⋅ A ) • I = − n ⋅( µ0 ⋅ n ⋅ ) ⋅ A l • A = −(n 2 ⋅ µ 0 ⋅ ) ⋅ I l I B = µ0 ⋅ n ⋅ l Cusanus-Gymnasium Wittlich Physik Die Induktion Die Selbstinduktion • • Ui = − n i( B⋅ A + B ⋅ A ) • I = − n ⋅ ( µ0 ⋅ n ⋅ ) ⋅ A l • A = −(n 2 ⋅ µ 0 ⋅ ) ⋅ I l • = −L⋅I Ui = − L ⋅ I s V A 1 = ] L [ • = 1H " Henry " I B = µ0 ⋅ n ⋅ l Cusanus-Gymnasium Wittlich Physik Die Induktion Die Selbstinduktion I B = µ0 ⋅ n ⋅ l Cusanus-Gymnasium Wittlich Physik Die Induktion Die Selbstinduktion -+