Hausübung 1

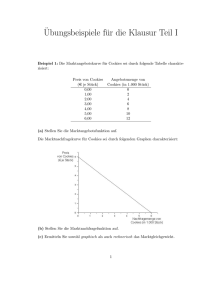
Hausübung 1
IK Ökonomische Entscheidungen und Märkte
WS 10/11
Beispiel 1.1 [3 P]: Die Marktnachfrage nach Schokolade sei durch folgende Tabelle
charakterisiert:
P =Preis
(€ je Pkg.)
0,00
1,00
2,00
3,00
4,00
5,00
6,00
7,00
8,00
9,00
10,00
QD = Nachfragemenge
(in 1 000 Pkg.)
5,00
4,50
4,00
3,50
3,00
2,50
2,00
1,50
1,00
0,50
0,00
a) Zeichnen Sie den Graphen zu dieser Marktnachfrage und stellen Sie die (inverse)
Marktnachfragefunktion auf!
Das Marktangebot nach Schokolade sei durch folgende Tabelle gegeben:
P =Preis
(€ je Pkg.)
2,00
3,00
4,00
5,00
6,00
7,00
8,00
QS = Angebotsmenge
(in 1 000 Pkg.)
0,00
0,50
1,00
1,50
2,00
2,50
3,00
b) Zeichnen Sie den Graphen zu dieser Marktangebotsfunktion und stellen Sie die
(inverse) Marktangebotsfunktion auf!
c) Ermitteln Sie das Marktgleichgewicht sowohl graphisch als auch rechnerisch!
Beispiel 1.2. [4 P]:
P] Die Nachfrage nach Yak-Butter ist durch QD = 150 − 3P gegeben, die
Angebotsfunktion lautet QS = 2 P − 50 . Die Mengen werden jeweils in 100-kg Einheiten
gemessen.
a) Zeichnen Sie die Nachfrage- und Angebotskurve zu obigen Funktionen in einem
Preis-Mengen-Diagramm und bestimmen Sie graphisch den Gleichgewichtspreis
(=P*) und die Gleichgewichtsmenge (=Q*) des Yak-Butter Marktes.
b) Ermitteln Sie rechnerisch das Gleichgewicht des Yak-Butter Marktes.
c) Die Hochsteppen und Kältewüsten Tibets – die traditionelle Heimat der Yaks –
werden von einer fürchterlichen Trockenheit heimgesucht. Die Angebotskurve
verschiebt sich auf QS′ = 2 P − 100 . Die Nachfragekurve bleibt unverändert. Ermitteln
Sie sowohl graphisch als auch rechnerisch das neue Gleichgewicht des Yak-Butter
Marktes.
d) Die Trockenheit ist vorüber, die Bestände der Yak-Herden haben sich erholt und die
Angebotskurve hat nun wieder die Form QS = 2 P − 50 . Der Großteil der
nachgefragten Yak-Butter wurde traditionell von den KonsumentInnen selbst zu
Butter-Tee verarbeitet. Da seit kurzem Coca-Cola in der Hochebene von Tibet
erhältlich ist (und sich großer Beliebtheit erfreut) hat die Nachfrage nach Yak-Butter
abgenommen und lautet nun QD′ = 120 − 3P . Ermitteln Sie das neue Gleichgewicht
sowohl graphisch als auch rechnerisch.
Beispiel 1.3. [3 P]:
P] Gegeben sei die Nachfragefunktion
Angebotsfunktion QS = 2 P − 1 .
Q D = −2 P + 7
und die
a) Berechnen Sie den Gleichgewichtspreis und die im Gleichgewicht gehandelte
Menge. Stellen Sie das Marktgleichgewicht auch graphisch dar.
b) Nehmen Sie an, der Preis des Gutes ist auf P = 3 bzw. P = 1 fixiert. Welche
Situation liegt dann jeweils vor? Welche Mengen werden bei diesen Preisen
jeweils gehandelt?