DMS - Dehnungsmessstreifen
Werbung

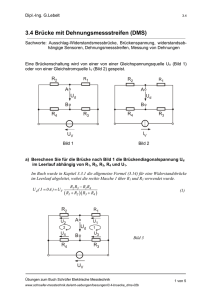
NTB Sensordatenbank / Labor Elektronische Messsysteme Sensor No. 02 Seite 1 DMS - Dehnungsmessstreifen Bezeichnungen: Metall-DMS, Halbleiter-DMS, Strain Gauges Messprinzip / Physikalisches Gesetz Der elektrische Widerstand jedes Leiters verändert sich bei Deformation. Die Ursache der Deformation kann eine Kraft, Druck, Drehmoment, Auslenkung, Drehwinkel usw. sein. Der Widerstand eines deformierten DMS setzt sich aus seinem Grundwiderstand R (unbelastet) und die durch die Deformation verursachte Widerstandsänderung ∆R zusammen. Skizze mechanisch / elektrisch l0 ∆l ∆r Bild 1: Zeigt die geometrische Deformation eines gedehnten Drahtes. Die relative Widerstandsänderung lässt sich aus der Änderung der Parameter für den elektrischen Widerstand eines 2 Drahtes R = ρ l / π r berechnen, wobei ρ den spezifischen Widerstand, l die Drahtlänge und r den Radius darstellt. ∆R 1 = R R bzw. é ∂R ù ∆ρ ∆l 2 ⋅ ∆r é ∆ρ ρ ∂R ∂R ù + 1+ 2 ⋅ µ ⋅ ε = k ⋅ ε ⋅ ∆r ú = + − =ê ⋅ ∆l + ⋅ ∆ρ + ⋅ê ∂r ρ ∂l l r ë ε ë ∂ρ R = R 0 ⋅ (1 + k ⋅ ε) mit den nachfolgenden Abkürzungen: Längendehnung ε = ∆l Dehungsempfindlichkeit k l es wird auch die Bezeichnung mikro-Dehnung µD für µm/m benutzt oder kurz k-Faktor (gauge factor) ∆ r r dem materialspezifischen Zusammenhang zw. Quer- und Längsdehnung Poisson-Zahl µ=− ∆l l Weil der k-Faktor im verwendeten Bereich der Dehnung annähernd als konstant betrachtet werden kann, ist die Widerstandsänderung proportional zur Dehnung. So kann beispielsweise aus einer Widerstandserhöhung um 0.2% auf eine Dehnung von 0.1% geschlossen werden, wenn k=2 gilt (DMS aus Konstantan). Die elektrische Widerstandsänderung ist auf zwei Ursachen zurückzuführen: •= Änderung der Leitergeometrie: Wird ein Draht gezogen, so verlängert sich dieser und der Querschnitt nimmt ab. •= Änderung der Leitfähigkeit des Materials bei mechanischer Beanspruchung: Durch die Deformation des Kristallgitters verändert sich die Beweglichkeit der freien Ladungsträger und damit die Leitfähigkeit des Materials (Piezoresistiver Effekt). Vor allem bei Halbleitern ist er sehr ausgeprägt und übertrifft den Einfluss der Geometrieänderung bei weitem. Als Widerstandsmaterial wird bei Dehnungsmessstreifen Metalle oder Halbleiter verwendet. Für DMS aus Konstantan ist k etwa 2 (mit µ ≈ 0.3 bei elastischer Verformung und (∆ρ/ρ)/ε ≈ 0.4 ). Beispielsweise hat die Legierung Nichrom V (80 Ni, 20 Cr) eine k-Faktor von etwa 2.2 während Platin Wolfram (92 Pt, 8W) einen k-Faktor von etwa 4 aufweist .[2] Halbleiter DMS können hohe k-Werte von bis zu 200 aufweisen, die auf die Veränderung des spezifischen Widerstandes bei Deformation zurückzuführen sind. Copyright bei Franz Baumgartner // e-mail: [email protected] // Fachhochschule Buchs / www.ntb.ch/Pubs/sensordemo/ 26-06-2001 NTB Sensordatenbank / Labor Elektronische Messsysteme Sensor No. 02 Seite 2 Prinzip / Bauform Bild 2: Varianten unterschiedlicher Gitter-Anordnungen; links ein in Pfeilrichtung einachsig empfindlicher DMS von VISHAY, daneben drei Beispiele von VISHAY zur Messung der Dehnung in mehr als einer Achse. In der Mitte ist die Rosetten-Form vergrössert dargestellt, die zweite Abbildung von rechts zeigt einen Standard DMS (Y-Stress 1grid) von HBM , ganz rechts ist ein hochempfindliches DMS Gitter von HBM (Serie K-high quality full bridge) zur Druckmessung dargestellt das gleichzeitig als Vollbrücke verschalten wird. vgl. auch [2] Metall-DMS Sie sind aus einer auf einem Trägerfilm aufgebrachten Metallfolie (z.B. Konstantan) herausgeätzt. Damit ein ausreichend hoher Widerstand erreicht wird, ist die Leiterbahn mäanderförmig ausgeführt. Die jeweilige Anwendung bestimmt Anordnung und Grösse des Gitters und damit vor allem die Querempfindlichkeit. Dabei ist die Querempfindlichkeit jener Fehler, der zu einer Widerstandserhöhung bei einer Deformation quer zur Messrichtung führt. Ein langes Messgitter mit wenig Umkehrstellen hat einen niedrigen, bzw. ein kurzes Messgitter mit vielen Umkehrstellen hat einen hohen Querempfindlichkeitsfaktor. Eine Verbreiterung des Querschnittes bei der Umkehrstelle reduziert ebenfalls die Querempfindlichkeit. Wie bereits oben erwähnt resultiert bei Metall-DMS die Widerstandsänderungen aus zwei ähnlich grossen Effekten, der Änderung der Leitergeometrie sowie der Änderung des spezifischen Widerstandes. Halbleiter-DMS Bei Halbleitermaterialien ist der piezoresistive Effekt sehr viel ausgeprägter als bei Metallen. Er hängt von der Orientierung des Halbleiter-Einkristalls und von der Dotierung (Art, Dichte und Verteilung der Fremdatome, welche die Leitfähigkeit bestimmen) ab. Bei ausgeführten Halbleiter-DMS ist der piezoresistive Effekt etwa 100 mal stärker als bei Metall-DMS. Halbleiter-DMS werden zur Druckmessung entweder ebenfalls auf eine solche Struktur aufgeklebt oder das Halbleitermaterial ist direkt aufgesputtert, so dass eine intensive Verbindung gewährleistet ist, was die Voraussetzung für Hysteresefreiheit, Alterungs- und Temperaturbeständigkeit ist. Es kann aber auch der gesamte Biegebalken in Silizium gefertigt sein, wobei die Leiterbahn des DMS durch Dotierung im Silizium gebildet werden kann. Aufbringen des DMS Die DMS werden meist mit Klebstoff am Messobjekt appliziert. Die Qualität der Klebstelle ist entscheidend für die erreichbare Genauigkeit. Die Oberfläche muss vor der Verklebung entsprechend präpariert werden und es empfiehlt sich die vom DMS-Hersteller empfohlenen Spezialklebstoffe zu verwenden. Schlechte Klebstellen oder ungeeigneter Klebstoff führen zu Kriechen, Hysterese und anderen Fehlern. Scheinbare Dehnung Die Angabe der scheinbaren Dehnung erlaubt eine einfache Bestimmung des zu erwartenden Messfehlers bei gegebener Temperaturänderung. Damit lässt sich der Temperaturfehler direkt mit der zu messenden Grösse, der Dehnung vergleichen. Eine ungewollte Widerstandsänderung kann bei einem DMS auftreten, wenn sich infolge einer Temperaturänderung der spezifische Widerstand ρ des DMS (α αR,DMS) ändert und die unterschiedliche Längendehnung des Messobjektes αObjekt und des DMS αDMS dies nicht kompensiert.(siehe unter Ergänzungen Bild 3.3-12) Bei einem DMS der auf einem Biegebalken appliziert ist, führt dies im unbelasteten Fall zu einem Nullpunktsfehler der von der Temperatur abhängt. Dieser Widerstandsänderung pro Grad K wird die scheinbare Dehnung εs zugeordnet : α é ù ε s = ∆T ⋅ êα Objekt − α DMS + R,DMS k ë Durch die Wahl der entsprechenden Legierungszusammensetzung des Metall-DMS kann für einen bestimmten Messobjektwerkstoff die scheinbare Dehnung zu Null kompensiert werden (selbst-Temperaturgangkompensierte DMS oder Bezeichnung S-T-C). Die scheinbare Dehnung ist vor allem bei der Messungen kleiner Dehnungen störend. Durch Einsatz von auf Zug und Druck belasteter DMS in Voll- oder Halbbrücken lassen sich diese Einflüsse zusätzlich minimieren. Copyright bei Franz Baumgartner // e-mail: [email protected] // Fachhochschule Buchs / www.ntb.ch/Pubs/sensordemo/ 26-06-2001 NTB Sensordatenbank / Labor Elektronische Messsysteme Sensor No. 02 Seite 3 Funktionsweisen / Produktvarianten Der DMS wird zur Messung der Kraft, Gewicht, Drehmoment oder der mechanischen Spannung bzw. des Drucks eingesetzt. Die jeweilige mechanische, physikalische Grösse, muss aus der Dehnung durch die Wahl der geeigneten DMS Geometrien ermittelt werden. Die Formeln für die Zusammenhänge zwischen Dehnung und der gewünschten Messgrösse sind der Fachliteratur sowie den technischen Unterlagen der renommierten DMS-Hersteller zu entnehmen [2,3,5]. Soll beispielsweise das Moment an einer Welle mit DMS gemessen werden, so bietet sich der Einsatz einer Geometrie an, bei der vier DMS im Winkel von 45° zur Achse angeordnet sind.(Seite 211 in [1]) Dabei werden je zwei DMS auf Druck und die beiden anderen auf Zug beansprucht. Brückenschaltung zur Messung der elektrischen Widerstandsänderung Die zur Dehnung proportionale Widerstandsänderung wird durch Strom- und Spannungsmessung oder mit Hilfe von Brücken- oder Kompensatorschaltungen gemessen. Werden DMS in einer Brückenschaltung (Wheatstonsche-Brücke siehe Bild 3) angeordnet, so kann erreicht werden, dass die Ausgangsspannung proportional zur Widerstandsänderung ∆R/R = δ ==ε⋅k und damit im Idealfall auch zur Dehnung ist. (Siehe Animation der Funktion unter Ergänzungen) Im ungedehnten Fall, Referenzwert δ=0 haben die vier Widerstände den gleichen Wert und damit wird auch die Ausgangsspannung Ua =0. Die Wheatstonsche-Brücke kann mit konstanter Spannung oder konstantem Strom gespeist werden. Bei Verwendung von vier Sensoren in der Vollbrücke ist der Wert der Ausgangsspannung um den Faktor vier größer als bei der Viertelbrücke mit nur einem Sensor, bei gleicher Dehnung und somit gleichem Wert δ=.(siehe Bild 3 und Tabelle 1) Die Schaltung der Viertelbrücke und der Quasihalbbrücke verursachen einen zusätzlichen Linearitätsfehler entsprechend der Formel in Tabelle 1. Dieser Linearitätsfehler beträgt ein Promille wenn der Dehnungsmessstreifens um ein Promille (1000 µD) gedehnt wird. Wird die Viertelbrücke mit einer konstanten Stromquelle versorgt kann der Linearitätsfehler im Vergleich zur Versorgung mit einer Spannungsquelle auf die Hälfte reduziert wird. Die Quasihalbbrücke, ebenfalls mit einer Stromquelle versorgt hat keinen systematischen Linearitätsfehler, gleich wie alle Schaltungsvarianten der Halb- und Vollbrücke. Viertelsbrücke Quasihalbbrücke R R(1+ÅF R R(1+ÅF Ua Halbbrücke R R Ub R(1+ÅF Ua R R(1+ÅF Ub Ib R R(1+ÅF Ua Vollbrücke Ua R R(1-ÅF R(1-ÅF Ub Ib R(1-ÅF R(1+ÅF Ub Ib Ib Bild 3: Vier Varianten von Brückenschaltungen aus[4] Tabelle 1: Ausgangsspannung 1) von DMS-Brückenschaltungen als Funktion der Dehnung (δ ==ε⋅k) [4] Viertelbrücke Quasihalbbrücke Halbbrücke Vollbrücke Spannungsquelle als Ua Ua Ua Ua δ δ δ =δ = = = Brückenversorgung Ub Stromquelle als Brückenversorgung 4 + 2⋅δ Ua δ = Ib ⋅ R 4 + δ Ub 2+δ Ua δ = Ib ⋅ R 2 Ub 2 Ua δ = Ib ⋅ R 2 Empfindlichkeit Linearitätsfehler ¼ ½ ½ mit Stromquelle mit Stromquelle Kein Lin. Fehler geringer Lin.Fehler kein Lin. Fehler 1) Formel gelten nur für stromlose, hochohmige Messung der Brückenmittenspannung Ua Ub Ua =δ Ib ⋅R 1 kein Lin Fehler Meistens werden Vollbrückenschaltungen angewendet, da mit diesen auch Störeinflüsse wie Temperatur, Kriechen am besten kompensiert werden können. Für die Messung sehr kleiner Dehnungen ist es notwendig, die Brücke mit Wechselspannung zu speisen (Instrumentenverstärker, Trägerfrequenzmessbrücke). Der Messstrom im DMS muss so bemessen sein, damit die thermischen Stromverluste I2·R pro Fläche gut abgeführt werden. Abhängig vom Material des Messobjektes sollte für eine hohe Messgenauigkeit bei statischer Messung diese flächenbezogene Verlustleistung für Aluminium < 3.1 mW/mm2 , Stahl < 1.6 mW/mm2 , Kunststoffe, GFK < 0.16 mW/mm2 sein [3] Copyright bei Franz Baumgartner // e-mail: [email protected] // Fachhochschule Buchs / www.ntb.ch/Pubs/sensordemo/ 26-06-2001 NTB Sensordatenbank / Labor Elektronische Messsysteme Sensor No. 02 Seite 4 Technische Daten kommerzieller Produkte Die DMS Hersteller bieten eine Vielzahl von DMS Typen an wobei z.B. über die Homepage (siehe Links) aus dem elektronischen Katalog ausgewählt werden kann. Auswahlkriterien sind Geometrie und damit die Messrichtung(en), Material des Messobjekts, Temperaturbereich, statische oder dynamische Messung, Messbereich der Dehnung. Auf die optimale Art der Verbindung des DMS mit dem Messobjekt, meist durch Kleben realisiert, ist besonders zu achten. Der Temperatur-Arbeitsbereich für stationäre Standard DMS liegt zwischen -75°C und +175°C. (Spezialausführungen von Folien-DMS bis 370°C) Materialermüdung des DMS setzt die Grenzen für wiederholte mechanische Wechselbeanspruchung. Die maximale Lastwechselzahl liegt zwischen 104 und 108, wobei sie um so grösser ist, je kleiner die Dehnung und je länger das Messgitter ist. Für konventionelle Folien-DMS liegt die maximale Lastwechselzahl bei einer zyklischen Dehnung von ± 2 mm/m bei 100 000 Zyklen. Die Änderung des k-Faktors mit der Temperatur und der Beharrungszeit (siehe Ergänzungen Bild 3.3-15 und 17) führen zu einem Empfindlichkeitsfehler der Messung. Zusätzlich kann die Einflussgrösse Temperatur über die scheinbare Dehnung einen Nullpunktsfehler verursachen. Nullpunktsfehler können aber auch von Toleranzschwankungen der Widerstandswerte im ungedehnten Fall sowie von einer mechanisch nicht spannungsfreier Montage des DMS am Messobjekt herrühren. Für verschiedene Anwendungen gibt es verschiedene Ausführungen von DMS. Die Länge des Messgitters liegt zwischen 0.6mm und 10mm (typische Abmessung 3.1mm x 2.6 mm für die Dehnungen in eine Richtungen, bis15.2 mm x 13.5 mm für Scherkraft- und Drehmomentsensoren - Rosettenform). Die DMS sind in einer Vielzahl von Kombinationen aus Gitterlegierungen (Konstantan-, Karma- ...) und Trägermaterialien (Polyimid, Epoxy ...) erhältlich, die für verschiedene Messobjekte (Stahl, Alu ..) eingesetzt werden. Für die Untersuchung von komplizierten Spannungszuständen, oder für besonders schwierige Anwendungsfälle, wurden unzählige Sonderformen entwickelt. Messbereich Metall-DMS: Max. Dehnung typisch <0.5% spezielle DMS bis plastischer Bereich der Verformung mit bis zu 20% Dehnung k-Faktor: 1.6...6.6; R = 60, 120, 175, 350, 500, 600, 700 Ohm Halbleiter-DMS: Max. Dehnung < 0.1% k-Faktor: -110...180; R = 120 , 350, 600, 700 Ohm Genauigkeit / Fehler Metall-DMS: Sehr linear, wenn k = 2 sogar im Bereich der plastischen Verformung (Beispiel: Konstantan-Hochdehnungs-DMS bei 10% Dehnung beträgt der Linearitätsfehler 10%); Nennwiderstandstoleranz:±0.2 %; Linearität:< ±0.02% v.EW; Hysterese:<±0.02% v.EW.; Wiederholbarkeit: < ±0.02 % v. EW.; Nullpunktfehler: <±0.02 % v EW.; Kriechen : < 0.05% pro 3 Minuten; k-Faktor ist temperaturabhängig. Halbleiter-DMS: Linear für Dehnungen < 0.05% (5% Linearätsfehler für Dehnung <0.1%) Temperatur /Umgebung Folien DMS, statische Messungen:-75 bis175°C; dynamische Messungen:-200 bis 250°C; Hochtemperatur-DMS bis 900 °C Je nach Anwendung unterschiedlich. Viele Sonderformen. Bauformen Metall-DMS: Konstantan (Cu,Ni) k=2.05; Karma(Ni,Cr,Fe,Al) k=2.1; Nichrom V (NiCr) k=2.2; Platin-Wolfram k=4 Metall-DMS: Fr. 7 bis Fr. 50; Halbleiter- DMS: Fr 10. bis Fr. 1000 Kosten (Für Stückzahlen >100 000 /a etwa Fr. 5 inkl. einfachem Alu-Biegebalken und Montage) Aufgrund des weit verbreiteten Einsatzes von DMS in den letzten Jahrzehnten besteht Vorteile eine enorme Auswahl an verschiedenen Arten von DMS, mit verschiedene Messgitter und verschiedenen Leitermaterialien; kostengünstig da hohe Stückzahlen; kleine Abmessungen; Das Aufbringen einer DMS ist sehr zeitintensiv. Lebensdauer ist beschränkt 10'000'000 Nachteile Zyklen (Ermüdung des DMS-Materials); Empfindlich auf mechanische Beanspruchung (überdehnen) Bei hoher Wechselbeanspruchung kann sich der DMS vom Träger lösen; Wägetechnik, Kraft-, Druck-, Drehmomentmesstechnik, mechanische Anwendungsbereiche Schwingungsanalyse, Auslenkungen Quellen, Links Literatur / Normen [1] J.Niebuhr, G.Lindner; Physikalische Messtechnik mit Sensoren; ISBN 3-486-23614-8; Auflage 1996 [2] K. Hoffmann, Eine Einführung in die Technik des Messens mit Dehnungsmessstreifen, Herausgeber: Hottinger Baldwin Messtechnik GmbH, Darmstadt 1987; Neuauflage August 2000, Anwendung und Einbau von Wägezellen, [3] Vishay, DMS Messtechnologie, Formel&Tabellen, Measurements Group Messtechnik, München 1991 [4] F. Baumgartner, K. Ruhm; Messen elektrischer Grössen; Handbuch der Industriellen Messtechnik, Oldenburg Verlag 2001 [5] E. Baumann; Elektrische Kraftmesstechnik; Seite 198, VEB Verlag Berlin, DDR 1976 [6] Experimentelle Strukturanalyse – Empfehlung DMS bei hohen Temperaturen; VDI/VDE/GESA 2635 Entwurf, 03/2001 Copyright bei Franz Baumgartner // e-mail: [email protected] // Fachhochschule Buchs / www.ntb.ch/Pubs/sensordemo/ 26-06-2001 NTB Sensordatenbank / Labor Elektronische Messsysteme Sensor No. 02 Seite 5 Hersteller / Distributoren Firmen Produkte Links HBM, Hottinger Baldwin Alle DMS Anwendungen, auch div. https://www.hbmwt.com/ Messtechnik, Darmstadt BRD Wägezellen, 40 Jahre Erfahrung http://www.measurementsgroup.com/guide/index.htm Vishay-Measurements Group, Alle DMS Raleigh, USA STRAINSERT, PA, USA http://www.Strainsert.com/ Denton Inc, USA http://radenton.com/ Erstellt: 1999-10-25 von Tobler und F. Baumgartner Überarbeitet: 2002-10-23 von F. Baumgartner / FH-Buchs / Labor Elektronische Messsysteme Ergänzungen Animation zur Funktion des DMS in der Brückenschaltung FH-Ulm, D : http://www.rz.fh-ulm.de/labore/mtech/Dms_anim.htm Formel und Berechnung verschiedener Wheatstone Schaltungstypen: http://www.measurementsgroup.com/guide/tn/tn507/507br0.htm Werkstoffkenngrössen E-Modul, Wärmedehnung, Poisson : http://www.measurementsgroup.com/guide/ta/mat/wcmatj.htm Widerstand der Sensorzuleitung: http://www.measurementsgroup.com/guide/ta/wt/wcwtj.htm Temperaturgang des K-Faktors : http://www.measurementsgroup.com/guide/tn/tn504/504index.htm Praktischer 2 σ Streubereich beträgt etwa 30 bis 50 µε:http://www.measurementsgroup.com/guide/tn/tn504/504h.htm Kraft und Momentmessung mit DMS: http://www.measurementsgroup.com/guide/ta/ftm/ftm.htm Temperaturgang selbstkompensierterSTC DMS, Vishay : http://www.measurementsgroup.com/guide/tn/tn505/505stc.htm Charakteristische Diagramme von DMS (Literaturquelle: K. Hoffmann; HBM 1987). Copyright bei Franz Baumgartner // e-mail: [email protected] // Fachhochschule Buchs / www.ntb.ch/Pubs/sensordemo/ 26-06-2001 NTB Sensordatenbank / Labor Elektronische Messsysteme Copyright bei Franz Baumgartner // e-mail: [email protected] // Fachhochschule Buchs / www.ntb.ch/Pubs/sensordemo/ Sensor No. 02 Seite 6 26-06-2001